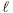 is the
log-likelihood and k is the total number of
parameters estimated. Note that X-12-ARIMA
does not produce information criteria such as AIC when estimation
is by conditional ML.
is the
log-likelihood and k is the total number of
parameters estimated. Note that X-12-ARIMA
does not produce information criteria such as AIC when estimation
is by conditional ML.
See also the Gretl Function Reference.
The following commands are documented below.
Note that brackets "[" and "]" are used to indicate that certain elements of commands are optional. The brackets should not be typed by the user.
| Argument: | varlist |
| Options: | --lm (do an LM test, OLS only) |
| --auto=criterion (forward stepwise, OLS only) | |
| --quiet (print only the basic test result) | |
| --silent (don't print anything) | |
| --vcv (print covariance matrix for augmented model) | |
| --both (IV estimation only, see below) | |
| Examples: | add 5 7 9 |
| add xx yy zz --quiet | |
| add xlist --auto=BIC |
Must be invoked after an estimation command. If neither of the --lm and --auto options are given, this command performs a joint test for the addition of the specified variables to the last model. An augmented version of the original model is estimated, including the variables in varlist, and a Wald test is carried out on the augmented model. The augmented model replaces the original as the "last model" for the purposes of, for example, retrieving the residuals as $uhat or doing further tests. The results of the Wald test may be retrieved using the accessors $test and $pvalue.
The --both option applies only if the last model was estimated via two-stage least squares: it specifies that the new variables should be added to the list of instruments as well as to the list of regressors, the default being to add them to the regressors only.
Given the --lm option (available only for models estimated via OLS), an LM test is performed. An auxiliary regression is run in which the dependent variable is the residual from the last model and the independent variables are those from the last model plus varlist. Under the null hypothesis that the added variables have no additional predictive power, the sample size times the unadjusted R-squared from this regression is distributed as chi-square with degrees of freedom equal to the number of added regressors. Under this option the original model is not replaced.
The --auto option (which cannot be combined with --lm) calls for forward stepwise regression, using the QR algorithm described by Hastie et al (2020). In this case varlist is interpreted as a list of candidates for addition to the original model. At each step the method determines which candidate offers the greatest improvement in fit according to the specified criterion (given as parameter to the option). The algorithm halts when no further improvement is possible. The criterion must take one of these forms:
An Information Criterion: AIC, BIC or HQC. The "best" candidate at each step is then that which gives the greatest improvement (reduction) in the selected criterion.
An α value (positive decimal fraction). In this case the figure of merit is the sum of squared residuals. The algorithm halts when no remaining candidate gives a reduction in SSR that is statistically significant at the α level on a chi-square test.
Menu path: Model window, /Tests/Add variables
| Arguments: | order varlist |
| Options: | --nc (test without a constant) |
| --c (with constant only) | |
| --ct (with constant and trend) | |
| --ctt (with constant, trend and trend squared) | |
| --seasonals (include seasonal dummy variables) | |
| --gls (de-mean or de-trend using GLS) | |
| --verbose (print regression results) | |
| --quiet (suppress printing of results) | |
| --difference (use first difference of variable) | |
| --test-down[=criterion] (automatic lag order) | |
| --perron-qu (see below) | |
| Examples: | adf 0 y |
| adf 2 y --nc --c --ct | |
| adf 12 y --c --test-down | |
| See also jgm-1996.inp |
The options shown above and the discussion which follows mostly pertain to the use of the adf command with regular time series data. For use of this command with panel data please see the section titled "Panel data" below.
This command computes a set of Dickey–Fuller tests on each of the listed variables, the null hypothesis being that the variable in question has a unit root. (But if the --difference flag is given, the first difference of the variable is taken prior to testing, and the discussion below must be taken as referring to the transformed variable.)
By default, two variants of the test are shown: one based on a regression containing a constant and one using a constant and linear trend. You can control the variants that are presented by specifying one or more of the option flags --nc, --c, --ct, --ctt.
The --gls option can be used in conjunction with one or other of the flags --c and --ct. The effect of this option is that the series to be tested is demeaned or detrended using the GLS procedure proposed by Elliott, Rothenberg and Stock (1996), which gives a test of greater power than the standard Dickey–Fuller approach. This option is not compatible with --nc, --ctt or --seasonals.
In all cases the dependent variable in the test regression is the first difference of the specified series, y, and the key independent variable is the first lag of y. The regression is constructed such that the coefficient on lagged y equals the root in question, α, minus 1. For example, the model with a constant may be written as
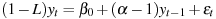
Under the null hypothesis of a unit root the coefficient on lagged y equals zero. Under the alternative that y is stationary this coefficient is negative. So the test is inherently one-sided.
The simplest version of the Dickey–Fuller test assumes that the error term in the test regression is serially uncorrelated. In practice this is unlikely to be the case and the specification is often extended by including one or more lags of the dependent variable, giving an Augmented Dickey–Fuller (ADF) test. The order argument governs the number of such lags, k, possibly depending on the sample size, T.
For a fixed, user-specified k: give a non-negative value for order.
For T-dependent k: give order as –1. The order is then set following the recommendation of Schwert (1989), namely the integer part of 12(T/100)0.25.
In general, however, we don't know how many lags will be required to "whiten" the Dickey–Fuller residual. It's therefore common to specify the maximum value of k and let the data decide the actual number of lags to include. This can be done via the --test-down option. The criterion for selecting optimal k may be set using the parameter to this option, which should be one of AIC, BIC or tstat, AIC being the default.
When testing down via AIC or BIC, the final lag order for the ADF equation is that which optimizes the chosen information criterion (Akaike or Schwarz Bayesian). The exact procedure depends on whether or not the --gls option is given. When GLS is specified, AIC and BIC are the "modified" versions described in Ng and Perron (2001), otherwise they are the standard versions. In the GLS case a refinement is available. If the additional option --perron-qu is given, lag-order selection is performed via the revised method recommended by Perron and Qu (2007). In this case the data are first demeaned or detrended via OLS; GLS is applied once the lag order is determined.
When testing down via the t-statistic method is called for, the procedure is as follows:
Estimate the Dickey–Fuller regression with k lags of the dependent variable.
Is the last lag significant? If so, execute the test with lag order k. Otherwise, let k = k – 1; if k equals 0, execute the test with lag order 0, else go to step 1.
In the context of step 2 above, "significant" means that the t-statistic for the last lag has an asymptotic two-sided p-value, against the normal distribution, of 0.10 or less.
To sum up, if we accept the various arguments of Perron, Ng, Qu and Schwert referenced above, the favored command for testing a series y is likely to be:
adf -1 y --c --gls --test-down --perron-qu
(Or substitute --ct for --c if the series seems to display a trend.) The lag order for the test will then be determined by testing down via modified AIC from the Schwert maximum, with the Perron–Qu refinement.
P-values for the Dickey–Fuller tests are based on response-surface estimates. When GLS is not applied these are taken from MacKinnon (1996). Otherwise they are taken from Cottrell (2015) or, when testing down is performed, Sephton (2021). The P-values are specific to the sample size unless they are labeled as asymptotic.
When the adf command is used with panel data, to produce a panel unit root test, the applicable options and the results shown are somewhat different.
First, while you may give a list of variables for testing in the regular time-series case, with panel data only one variable may be tested per command. Second, the options governing the inclusion of deterministic terms become mutually exclusive: you must choose between no-constant, constant only, and constant plus trend; the default is constant only. In addition, the --seasonals option is not available. Third, the --verbose option has a different meaning: it produces a brief account of the test for each individual time series (the default being to show only the overall result).
The overall test (null hypothesis: the series in question has a unit root for all the panel units) is calculated in one or both of two ways: using the method of Im, Pesaran and Shin (Journal of Econometrics, 2003) or that of Choi (Journal of International Money and Finance, 2001). The Choi test requires that P-values are available for the individual tests; if this is not the case (depending on the options selected) it is omitted. The particular statistic given for the Im, Pesaran, Shin test varies as follows: if the lag order for the test is non-zero their W statistic is shown; otherwise if the time-series lengths differ by individual, their Z statistic; otherwise their t-bar statistic. See also the levinlin command.
Menu path: /Variable/Unit root tests/Augmented Dickey-Fuller test
| Arguments: | response treatment [ block ] |
| Option: | --quiet (don't print results) |
Analysis of Variance: response is a series measuring some effect of interest and treatment must be a discrete variable that codes for two or more types of treatment (or non-treatment). For two-way ANOVA, the block variable (which should also be discrete) codes for the values of some control variable.
Unless the --quiet option is given, this command prints a table showing the sums of squares and mean squares along with an F-test. The F-test and its p-value can be retrieved using the accessors $test and $pvalue respectively.
The null hypothesis for the F-test is that the mean response is invariant with respect to the treatment type, or in words that the treatment has no effect. Strictly speaking, the test is valid only if the variance of the response is the same for all treatment types.
Note that the results shown by this command are in fact a subset of the information given by the following procedure, which is easily implemented in gretl. Create a set of dummy variables coding for all but one of the treatment types. For two-way ANOVA, in addition create a set of dummies coding for all but one of the "blocks". Then regress response on a constant and the dummies using ols. For a one-way design the ANOVA table is printed via the --anova option to ols. In the two-way case the relevant F-test is found by using the omit command. For example (assuming y is the response, xt codes for the treatment, and xb codes for blocks):
# one-way list dxt = dummify(xt) ols y 0 dxt --anova # two-way list dxb = dummify(xb) ols y 0 dxt dxb # test joint significance of dxt omit dxt --quiet
Menu path: /Model/Other linear models/ANOVA
| Argument: | filename |
| Options: | --time-series (see below) |
| --fixed-sample (see below) | |
| --update-overlap (see below) | |
| --quiet (print less confirmation details, see below) | |
| See below for additional specialized options |
Opens a data file and appends the content to the current dataset, if the new data are compatible. The program will try to detect the format of the data file (native, plain text, CSV, Gnumeric, Excel, etc.). Please note that the join command offers much more control over the matching of supplementary data to the current dataset. Also note that appending data to an existing panel dataset is potentially quite tricky; see the section headed "Panel data" below.
The appended data may take the form of either additional observations on series already present in the dataset, and/or new series. In the case of adding series, compatibility requires either (a) that the number of observations for the new data equals that for the current data, or (b) that the new data carries clear observation information so that gretl can work out how to place the values. Note that if there's a "perfect match" of observation information (that is, conditions (a) and (b) are both satisfied), it is assumed that series, rather than observations, are to be added. And if it happens that there are no series names in the file whose data are to be appended that are not already present in the current dataset then nothing is done, and a warning is shown.
One case that is not supported is where the new data start earlier and also end later than the original data. To add new series in such a case you can use the --fixed-sample option; this has the effect of suppressing the adding of observations, and so restricting the operation to the addition of new series.
When a data file is selected for appending, there may be an area of overlap with the existing dataset; that is, one or more series may have one or more observations in common across the two sources. If the option --update-overlap is given, the append operation will replace any overlapping observations with the values from the selected data file, otherwise the values currently in place will be unaffected.
The additional specialized options --sheet, --coloffset, --rowoffset and --fixed-cols work in the same way as with open; see that command for explanations.
By default some information about the appended dataset is printed. The --quiet option reduces that printout to a confirmatory message stating just the path to the file. If you want the operation to be completely silent, then issue the command set verbose off before appending the data, in combination with the --quiet option.
When new data are appended to a panel dataset, the result will be correct only if both the "units" or "individuals" and the time-periods are properly matched.
Two relatively simple cases should be handled correctly by append. Let N denote the number of cross-sectional units and T denote the number of time periods in the current panel, and let m denote the number of observations for the new data. If m = N the new data are taken to be time-invariant, and are copied into place for each time period. On the other hand, if m = T the data are treated as invariant across the panel units, and are copied into place for each unit. If T = N an ambiguity arises. In that case the new data are treated as time-invariant by default, but you can force gretl to treat them as time series (invariant across the units) via the --time-series option.
If the current dataset and the incoming data are both recognized as panel data then appending is supported only if both the T and N dimensions match; otherwise an error is flagged. For more complex cases use join instead of append.
Menu path: /File/Append data
| Arguments: | lags ; depvar indepvars |
| Options: | --vcv (print covariance matrix) |
| --quiet (don't print parameter estimates) | |
| Example: | ar 1 3 4 ; y 0 x1 x2 x3 |
Computes parameter estimates using the generalized Cochrane–Orcutt iterative procedure; see Section 9.5 of Ramanathan (2002). Iteration is terminated when successive error sums of squares do not differ by more than 0.005 percent or after 20 iterations.
lags is a list of lags in the residuals, terminated by a semicolon. In the above example, the error term is specified as
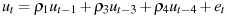
Menu path: /Model/Univariate time series/AR Errors (GLS)
| Arguments: | depvar indepvars |
| Options: | --hilu (use Hildreth–Lu procedure) |
| --pwe (use Prais–Winsten estimator) | |
| --vcv (print covariance matrix) | |
| --no-corc (do not fine-tune results with Cochrane-Orcutt) | |
| --loose (use looser convergence criterion) | |
| --quiet (don't print anything) | |
| Examples: | ar1 1 0 2 4 6 7 |
| ar1 y 0 xlist --pwe | |
| ar1 y 0 xlist --hilu --no-corc |
Computes feasible GLS estimates for a model in which the error term is assumed to follow a first-order autoregressive process.
The default method is the Cochrane–Orcutt iterative procedure; see for example section 9.4 of Ramanathan (2002). The criterion for convergence is that successive estimates of the autocorrelation coefficient do not differ by more than 1e-6, or if the --loose option is given, by more than 0.001. If this is not achieved within 100 iterations an error is flagged.
If the --pwe option is given, the Prais–Winsten estimator is used. This involves an iteration similar to Cochrane–Orcutt; the difference is that while Cochrane–Orcutt discards the first observation, Prais–Winsten makes use of it. See, for example, Chapter 13 of Greene (2000) for details.
If the --hilu option is given, the Hildreth–Lu search procedure is used. The results are then fine-tuned using the Cochrane–Orcutt method, unless the --no-corc flag is specified. The --no-corc option is ignored for estimators other than Hildreth–Lu.
Menu path: /Model/Univariate time series/AR Errors (GLS)
| Arguments: | order depvar indepvars |
| Option: | --quiet (don't print anything) |
| Example: | arch 4 y 0 x1 x2 x3 |
This command is retained at present for backward compatibility, but you are better off using the maximum likelihood estimator offered by the garch command; for a plain ARCH model, set the first GARCH parameter to 0.
Estimates the given model specification allowing for ARCH (Autoregressive Conditional Heteroskedasticity). The model is first estimated via OLS, then an auxiliary regression is run, in which the squared residual from the first stage is regressed on its own lagged values. The final step is weighted least squares estimation, using as weights the reciprocals of the fitted error variances from the auxiliary regression. (If the predicted variance of any observation in the auxiliary regression is not positive, then the corresponding squared residual is used instead).
The alpha values displayed below the coefficients are the estimated parameters of the ARCH process from the auxiliary regression.
See also garch and modtest (the --arch option).
| Arguments: | p d q [ ; P D Q ] ; depvar [ indepvars ] |
| Options: | --verbose (print details of iterations) |
| --quiet (don't print out results) | |
| --vcv (print covariance matrix) | |
| --hessian (see below) | |
| --opg (see below) | |
| --nc (do not include a constant) | |
| --conditional (use conditional maximum likelihood) | |
| --x-12-arima (use X-12-ARIMA, or X13, for estimation) | |
| --lbfgs (use L-BFGS-B maximizer) | |
| --y-diff-only (ARIMAX special, see below) | |
| --lagselect (see below) | |
| Examples: | arima 1 0 2 ; y |
| arima 2 0 2 ; y 0 x1 x2 --verbose | |
| arima 0 1 1 ; 0 1 1 ; y --nc | |
| See also armaloop.inp, auto_arima.inp, bjg.inp |
Note: arma is an acceptable alias for this command.
If no indepvars list is given, estimates a univariate ARIMA (Autoregressive, Integrated, Moving Average) model. The values p, d and q represent the autoregressive (AR) order, the differencing order, and the moving average (MA) order respectively. These values may be given in numerical form, or as the names of pre-existing scalar variables. A d value of 1, for instance, means that the first difference of the dependent variable should be taken before estimating the ARMA parameters.
If you wish to include only specific AR or MA lags in the model (as opposed to all lags up to a given order) you can substitute for p and/or q either (a) the name of a pre-defined matrix containing a set of integer values or (b) an expression such as {1,4}; that is, a set of lags separated by commas and enclosed in braces.
The optional integer values P, D and Q represent the seasonal AR order, the order for seasonal differencing, and the seasonal MA order, respectively. These are applicable only if the data have a frequency greater than 1 (for example, quarterly or monthly data). These orders may be given in numerical form or as scalar variables.
In the univariate case the default is to include an intercept in the model but this can be suppressed with the --nc flag. If indepvars are added, the model becomes ARMAX; in this case the constant should be included explicitly if you want an intercept (as in the second example above).
An alternative form of syntax is available for this command: if you do not want to apply differencing (either seasonal or non-seasonal), you may omit the d and D fields altogether, rather than explicitly entering 0. In addition, arma is a synonym or alias for arima. Thus for example the following command is a valid way to specify an ARMA(2, 1) model:
arma 2 1 ; y
The default is to use the "native" gretl ARMA functionality, with estimation by exact ML; estimation via conditional ML is available as an option. (If X-12-ARIMA is installed you have the option of using it instead of native code. Note that the newer X13 works as a drop-in replacement in exactly the same way.) For details regarding these options, please see chapter 31 of the Gretl User's Guide.
When native exact ML code is used, estimated standard errors are by default based on a numerical approximation to the (negative inverse of) the Hessian, with a fallback to the outer product of the gradient (OPG) if calculation of the numerical Hessian should fail. Two (mutually exclusive) option flags can be used to force the issue: the --opg option forces use of the OPG method, with no attempt to compute the Hessian, while the --hessian flag disables the fallback to OPG. Note that failure of the numerical Hessian computation is generally an indicator of a misspecified model.
The option --lbfgs is specific to estimation using native ARMA code and exact ML: it calls for use of the "limited memory" L-BFGS-B algorithm in place of the regular BFGS maximizer. This may help in some instances where convergence is difficult to achieve.
The option --y-diff-only is specific to estimation of ARIMAX models (models with a non-zero order of integration and including exogenous regressors), and applies only when gretl's native exact ML is used. For such models the default behavior is to difference both the dependent variable and the regressors, but when this option is specified only the dependent variable is differenced, the regressors remaining in level form.
The AIC value given in connection with ARIMA models is calculated according to the definition used in X-12-ARIMA, namely
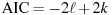
where
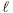 is the
log-likelihood and k is the total number of
parameters estimated. Note that X-12-ARIMA
does not produce information criteria such as AIC when estimation
is by conditional ML.
is the
log-likelihood and k is the total number of
parameters estimated. Note that X-12-ARIMA
does not produce information criteria such as AIC when estimation
is by conditional ML.
The AR and MA roots shown in connection with ARMA estimation are based on the following representation of an ARMA(p, q) process:
(1 - a_1*L - a_2*L^2 - ... - a_p*L^p)Y =
c + (1 + b_1*L + b_2*L^2 + ... + b_q*L^q) e_t
The AR roots are therefore the solutions to
1 - a_1*z - a_2*z^2 - ... - a_p*L^p = 0
and stability requires that these roots lie outside the unit circle.
The "frequency" figure printed in connection with AR and MA roots is the λ value that solves z = r * exp(i*2*π*λ) where z is the root in question and r is its modulus.
When the --lagselect option is given, this command does not give specific estimates, but instead produces a table showing information criteria and log-likelihood for a number of ARMA or ARIMA specifications. The lag orders p and q are taken as maxima; and if a seasonal specification is provided P and Q are also taken as maxima. In each case the minimum order is taken to be 0, and results are shown for all specifications from mimima to maxima. The degrees of differencing in the command, d and/or D, are respected but not treated as subject to search. A matrix holding the results is available via the $test accessor.
Menu path: /Model/Univariate time series/ARIMA
See arima; arma is an alias.
| Arguments: | order x |
| Options: | --corr1=rho (see below) |
| --sdcrit=multiple (see below) | |
| --boot=N (see below) | |
| --matrix=m (use matrix input) | |
| --quiet (suppress printing of results) | |
| Examples: | bds 5 x |
| bds 3 --matrix=m | |
| bds 4 --sdcrit=2.0 |
Performs the BDS (Brock, Dechert, Scheinkman and LeBaron, 1996) test for nonlinearity of the series x. In an econometric context this is typically used to test a regression residual for violation of the IID condition. The test is based on a set of correlation integrals, designed to detect nonlinearity of progressively higher dimensionality, and the order argument sets the number of such integrals. This must be at least 2; the first integral establishes a baseline but does not support a test. The BDS test is of the portmanteau type: able to detect all manner of departures from linearity but not informative about how exactly the condition was violated.
Instead of giving x as a series, the --matrix option can be used to specify a matrix as input. The matrix must be a vector (column or row).
The correlation integrals are based on a measure of "closeness" of data points, where two points are considered close if they lie within ε of each other. The test requires a specification of ε. By default gretl follows the recommendation of Kanzler (1999): ε is chosen such that the first-order correlation integral is around 0.7. A common alternative (requiring less computation) is to specify ε as a multiple of the standard deviation of the target series. The --sdcrit option supports the latter method; in the third example above ε is set to twice the standard deviation of x. The --corr1 option implies use of Kanzler's method but allows for a target correlation other than 0.7. It should be clear that these two options are mutually exclusive.
BDS test statistics are asymptotically distributed as N(0,1) but the test over-rejects quite markedly in small to moderate-sized samples. For that reason P-values are by default obtained via bootstrapping when x is of length less than 600 (but by reference to the normal distribution otherwise). If you want to use the bootstrap for larger samples you can force the issue by giving a non-zero value for the --boot option, Conversely, if you don't want bootstrapping for smaller samples, give a zero value for --boot.
When bootstrapping is performed the default number of iterations is 1999, but you can specify a different number by giving a value greater than 1 with --boot.
On successful completion of this command, $result retrieves the test results in the form of a matrix with two rows and order – 1 columns. The first row contains test statistics and the second P-values for each of the per-dimension tests under the null that x is linear/IID.
| Arguments: | depvar1 depvar2 indepvars1 [ ; indepvars2 ] |
| Options: | --vcv (print covariance matrix) |
| --robust (robust standard errors) | |
| --cluster=clustvar (see logit for explanation) | |
| --opg (see below) | |
| --save-xbeta (see below) | |
| --verbose (print extra information) | |
| Examples: | biprobit y1 y2 0 x1 x2 |
| biprobit y1 y2 0 x11 x12 ; 0 x21 x22 | |
| See also biprobit.inp |
Estimates a bivariate probit model, using the Newton–Raphson method to maximize the likelihood.
The argument list starts with the two (binary) dependent variables, followed by a list of regressors. If a second list is given, separated by a semicolon, this is interpreted as a set of regressors specific to the second equation, with indepvars1 being specific to the first equation; otherwise indepvars1 is taken to represent a common set of regressors.
By default, standard errors are computed using the analytical Hessian at convergence. But if the --opg option is given the covariance matrix is based on the Outer Product of the Gradient (OPG), or if the --robust option is given QML standard errors are calculated, using a "sandwich" of the inverse of the Hessian and the OPG.
Note that the estimate of rho, the correlation of the error terms across the two equations, is included in the coefficient vector; it's the last element in the accessors coeff, stderr and vcv.
After successful estimation, the accessor $uhat retrieves a matrix with two columns holding the generalized residuals for the two equations; that is, the expected values of the disturbances conditional on the observed outcomes and covariates. By default $yhat retrieves a matrix with four columns, holding the estimated probabilities of the four possible joint outcomes for (y1, y2), in the order (1,1), (1,0), (0,1), (0,0). Alternatively, if the option --save-xbeta is given, $yhat has two columns and holds the values of the index functions for the respective equations.
The output includes a test of the null hypothesis that the disturbances in the two equations are uncorrelated. This is a likelihood ratio test unless the QML variance estimator is requested, in which case it's a Wald test.
| Option: | --quiet (don't print anything) |
| Examples: | longley.inp |
Must follow the estimation of a model which includes at least two independent variables. Calculates and displays diagnostic information pertaining to collinearity, namely the BKW Table, based on the work of Belsley, Kuh and Welsch (1980). This table presents a sophisticated analysis of the degree and sources of collinearity, via eigenanalysis of the inverse correlation matrix. For a thorough account of the BKW approach with reference to gretl, and with several examples, see Adkins, Waters and Hill (2015).
Following this command the $result accessor may be used to retrieve the BKW table as a matrix. See also the vif command for a simpler approach to diagnosing collinearity.
There is also a function named bkw which offers greater flexibility.
Menu path: Model window, /Analysis/Collinearity
| Argument: | varlist |
| Options: | --notches (show 90 percent interval for median) |
| --factorized (see below) | |
| --panel (see below) | |
| --matrix=name (plot columns of named matrix) | |
| --output=filename (send output to specified file) |
These plots display the distribution of a variable. The central box encloses the middle 50 percent of the data, i.e. it is bounded by the first and third quartiles. The "whiskers" extend from each end of the box for a range equal to 1.5 times the interquartile range. Observations outside that range are considered outliers and represented via dots. A line is drawn across the box at the median. A "+" sign is used to indicate the mean. If the option of showing a confidence interval for the median is selected, this is computed via the bootstrap method and shown in the form of dashed horizontal lines above and/or below the median.
The --factorized option allows you to examine the distribution of a chosen variable conditional on the value of some discrete factor. For example, if a data set contains wages and a gender dummy variable you can select the wage variable as the target and gender as the factor, to see side-by-side boxplots of male and female wages, as in
boxplot wage gender --factorized
Note that in this case you must specify exactly two variables, with the factor given second.
If the current data set is a panel, and just one variable is specified, the --panel option produces a series of side-by-side boxplots, one for each panel "unit" or group.
Generally, the argument varlist is required, and refers to one or more series in the current dataset (given either by name or ID number). But if a named matrix is supplied via the --matrix option this argument becomes optional: by default a plot is drawn for each column of the specified matrix.
Gretl's boxplots are generated using gnuplot, and it is possible to specify the plot more fully by appending additional gnuplot commands, enclosed in braces. For details, please see the help for the gnuplot command.
In interactive mode the result is displayed immediately. In batch mode the default behavior is that a gnuplot command file is written in the user's working directory, with a name on the pattern gpttmpN.plt, starting with N = 01. The actual plots may be generated later using gnuplot (under MS Windows, wgnuplot). This behavior can be modified by use of the --output=filename option. For details, please see the gnuplot command.
Menu path: /View/Graph specified vars/Boxplots
Break out of a loop. This command can be used only within a loop; it causes command execution to break out of the current (innermost) loop. See also loop, continue.
| Syntax: | catch command |
This is not a command in its own right but can be used as a prefix to most regular commands: the effect is to prevent termination of a script if an error occurs in executing the command. If an error does occur, this is registered in an internal error code which can be accessed as $error (a zero value indicates success). The value of $error should always be checked immediately after using catch, and appropriate action taken if the command failed.
The catch keyword cannot be used before if, elif or endif. In addition it should not be used on calls to user-defined functions; it is intended for use only with gretl commands and calls to "built-in" functions or operators. Furthermore, catch cannot be used in conjunction with "back-arrow" assignment of models or plots to session icons (see chapter 3 of the Gretl User's Guide).
| Variants: | chow obs |
| chow dummyvar --dummy | |
| Options: | --dummy (use a pre-existing dummy variable) |
| --quiet (don't print estimates for augmented model) | |
| --limit-to=list (limit test to subset of regressors) | |
| Examples: | chow 25 |
| chow 1988:1 | |
| chow female --dummy |
Must follow an OLS regression. If an observation number or date is given, provides a test for the null hypothesis of no structural break at the given split point. The procedure is to create a dummy variable which equals 1 from the split point specified by obs to the end of the sample, 0 otherwise, and also interaction terms between this dummy and the original regressors. If a dummy variable is given, tests the null hypothesis of structural homogeneity with respect to that dummy. Again, interaction terms are added. In either case an augmented regression is run including the additional terms.
By default an F statistic is calculated, taking the augmented regression as the unrestricted model and the original as the restricted. But if the original model used a robust estimator for the covariance matrix, the test statistic is a Wald chi-square value based on a robust estimator of the covariance matrix for the augmented regression.
The --limit-to option can be used to limit the set of interactions with the split dummy variable to a subset of the original regressors. The parameter for this option must be a named list, all of whose members are among the original regressors. The list should not include the constant.
Menu path: Model window, /Tests/Chow test
| Options: | --dataset (clear dataset only) |
| --functions (clear functions (only)) | |
| --all (clear everything) |
By default this command clears the current dataset (if any) plus all saved variables (scalars, matrices, etc.) out of memory. Note that opening a new dataset, or using the nulldata command to create an empty dataset, also has this effect, so explicit use of clear is not usually necessary.
If the --dataset option is given, then only the dataset is cleared (plus any named lists of series); other saved objects such as matrices, scalars and bundles are preserved.
If the --functions option is given, then any user-defined functions, and any functions defined by packages that have been loaded, are cleared out of memory. The dataset and other variables are not affected.
If the --all option is given, clearing is comprehensive: the dataset, saved variables of all kinds, plus user-defined and packaged functions.
| Argument: | varlist |
| Option: | --quiet (don't print anything) |
| Examples: | coeffsum xt xt_1 xr_2 |
| See also restrict.inp |
Must follow a regression. Calculates the sum of the coefficients on the variables in varlist. Prints this sum along with its standard error and the p-value for the null hypothesis that the sum is zero.
Note the difference between this and omit, which tests the null hypothesis that the coefficients on a specified subset of independent variables are all equal to zero.
The --quiet option may be useful if one just wants access to the $test and $pvalue values that are recorded on successful completion.
Menu path: Model window, /Tests/Sum of coefficients
| Arguments: | order depvar indepvars |
| Options: | --nc (do not include a constant) |
| --ct (include constant and trend) | |
| --ctt (include constant and quadratic trend) | |
| --seasonals (include seasonal dummy variables) | |
| --skip-df (no DF tests on individual variables) | |
| --test-down[=criterion] (automatic lag order) | |
| --verbose (print extra details of regressions) | |
| --silent (don't print anything) | |
| Examples: | coint 4 y x1 x2 |
| coint 0 y x1 x2 --ct --skip-df |
The Engle–Granger (1987) cointegration test. The default procedure is: (1) carry out Dickey–Fuller tests on the null hypothesis that each of the variables listed has a unit root; (2) estimate the cointegrating regression; and (3) run a DF test on the residuals from the cointegrating regression. If the --skip-df flag is given, step (1) is omitted.
If the specified lag order is positive all the Dickey–Fuller tests use that order, with this qualification: if the --test-down option is given, the given value is taken as the maximum and the actual lag order used in each case is obtained by testing down. See the adf command for details of this procedure.
By default, the cointegrating regression contains a constant. If you wish to suppress the constant, add the --nc flag. If you wish to augment the list of deterministic terms in the cointegrating regression with a linear or quadratic trend, add the --ct or --ctt flag. These option flags are mutually exclusive. You also have the option of adding seasonal dummy variables (in the case of quarterly or monthly data).
P-values for this test are based on MacKinnon (1996). The relevant code is included by kind permission of the author.
For the cointegration tests due to Søren Johansen, see johansen.
Menu path: /Model/Multivariate time series
This command can be used only within a loop; it has the effect of skipping the subsequent statements within the current iteration of the current (innermost) loop. See also loop, break
| Variants: | corr [ varlist ] |
| corr --matrix=matname | |
| Options: | --uniform (ensure uniform sample) |
| --spearman (Spearman's rho) | |
| --kendall (Kendall's tau) | |
| --verbose (print rankings) | |
| --plot=mode-or-filename (see below) | |
| --triangle (only plot lower half, see below) | |
| --quiet (do not print anything) | |
| Examples: | corr y x1 x2 x3 |
| corr ylist --uniform | |
| corr x y --spearman | |
| corr --matrix=X --plot=display |
By default, prints the pairwise correlation coefficients (Pearson's product-moment correlation) for the variables in varlist, or for all variables in the data set if varlist is not given. The standard behavior is to use all available observations for computing each pairwise coefficient, but if the --uniform option is given the sample is limited (if necessary) so that the same set of observations is used for all the coefficients. This option has an effect only if there are differing numbers of missing values for the variables used.
The (mutually exclusive) options --spearman and --kendall produce, respectively, Spearman's rank correlation rho and Kendall's rank correlation tau in place of the default Pearson coefficient. When either of these options is given, varlist should contain just two variables.
When a rank correlation is computed, the --verbose option can be used to print the original and ranked data (otherwise this option is ignored).
If varlist contains more than two series and gretl is not in batch mode, a "heatmap" plot of the correlation matrix is shown. This can be adjusted via the --plot option. The acceptable parameters to this option are none (to suppress the plot); display (to display a plot even when in batch mode); or a file name. The effect of providing a file name is as described for the --output option of the gnuplot command. When plotting is active the option --triangle can be used to show only the lower triangle of the matrix plot.
If the alternative form is given, using a named matrix rather than a list of series, the --spearman and --kendall options are not available—but see the npcorr function.
The $result accessor can be used to obtain the correlations as a matrix. Note that if it's this matrix that's of interest, not just the pairwise coefficients, then in the presence of missing values it's advisable to use the --uniform option. Unless a single, common sample is used it is not guaranteed that the correlation matrix will be positive semidefinite, as it ought to be by construction.
Menu path: /View/Correlation matrix
Other access: Main window pop-up menu (multiple selection)| Arguments: | y [ order ] |
| Options: | --plot=mode-or-filename (see below) |
| --quiet (don't print anything) | |
| --acf-only (omit partial autocorrelations) | |
| --bartlett (use Bartlett standard errors) | |
| Examples: | corrgm x 12 |
| corrgm GDP 12 --acf-only |
Prints and/or graphs the values of the autocorrelation function (ACF) for the series y, which may be specified by name or number. The values are defined as ρ(ut, ut-s) where ut is the tth observation of the variable u and s denotes the number of lags.
Unless the --acf-only option is given, partial autocorrelations (PACF, calculated using the Durbin–Levinson algorithm) are also shown: these are net of the effects of intervening lags.
Asterisks are used to indicate statistical significance of the individual autocorrelations. By default this is assessed using a standard error of one over the square root of the sample size, but if the --bartlett option is given then Bartlett standard errors are used for the ACF; see below for details. This option also governs the confidence band drawn in the ACF plot, if applicable. In addition the Ljung–Box Q statistic is shown; this tests the null that the series is "white noise" up to the given lag.
If an order value is specified the length of the correlogram is limited to at most that number of lags, otherwise the length is determined automatically, as a function of the frequency of the data and the number of observations.
Please note that in this context Bartlett standard errors are not just a robust variant of the default ones. The default standard errors pertain to the null hypothesis that the series in question is white noise; roughly speaking, this is not rejected at the 5 percent level if no more than 5 percent of the ACF values exceed the bounds set at 1.96 times the standard error. The Bartlett values, however, are associated with the hypothesis that the series follows a moving average process. Specifically, if the ACF values fall within the Bartlett bounds for lags greater than k, we fail to reject the null that y is MA(k). See chapter 7 of Brockwell and Davis (1987) for more on this point.
By default, if gretl is not in batch mode a plot of the correlogram is shown. This can be adjusted via the --plot option. The acceptable parameters to this option are none (to suppress the plot); display (to show a plot even when in batch mode); or a file name. The effect of providing a file name is as described for the --output option of the gnuplot command.
Upon successful completion, the accessors $test and $pvalue can be used to retrieve the Q statistic and its P-value, evaluated at the maximum lag. Note that if you just want this test you can use use the ljungbox function instead.
Menu path: /Variable/Correlogram
Other access: Main window pop-up menu (single selection)| Options: | --squares (perform the CUSUMSQ test) |
| --quiet (just print the Harvey–Collier test) | |
| --plot=mode-or-filename (see below) |
Must follow the estimation of a model via OLS. Performs the CUSUM test—or if the --squares option is given, the CUSUMSQ test—for parameter stability. A series of one-step ahead forecast errors is obtained by running a series of regressions: the first regression uses the first k observations and is used to generate a prediction of the dependent variable at observation k + 1; the second uses the first k + 1 observations and generates a prediction for observation k + 2, and so on (where k is the number of parameters in the original model).
The cumulated sum of the scaled forecast errors, or the squares of these errors, is printed. The null hypothesis of parameter stability is rejected at the 5 percent significance level if the cumulated sum strays outside of the 95 percent confidence band.
In the case of the CUSUM test, the Harvey–Collier t-statistic for testing the null hypothesis of parameter stability is also printed. See Greene's Econometric Analysis for details. For the CUSUMSQ test, the 95 percent confidence band is calculated using the algorithm given in Edgerton and Wells (1994).
By default, if gretl is not in batch mode a plot of the cumulated series and confidence band is shown. This can be adjusted via the --plot option. The acceptable parameters to this option are none (to suppress the plot); display (to display a plot even when in batch mode); or a file name. The effect of providing a file name is as described for the --output option of the gnuplot command.
Menu path: Model window, /Tests/CUSUM(SQ)
| Argument: | varlist |
| Options: | --compact=method (specify compaction method) |
| --quiet (don't report results except on error) | |
| --name=identifier (rename imported series) | |
| --odbc (import from ODBC database) | |
| --no-align (ODBC-specific, see below) |
Reads the variables in varlist from a database file (native gretl, RATS 4.0 or PcGive), which must have been opened previously using the open command. The data command can also be used to import series from DB.NOMICS or from an ODBC database; for details on those variants see gretl + DB.NOMICS or chapter 43 of the Gretl User's Guide, respectively.
The data frequency and sample range may be established via the setobs and smpl commands prior to using this command. Here's an example:
open fedstl.bin setobs 12 2000:01 smpl ; 2019:12 data unrate cpiaucsl
The commands above open the database named fedstl.bin (which is supplied with gretl), establish a monthly dataset starting in January 2000 and ending in December of 2019, and then import the series named unrate (unemployment rate) and cpiaucsl (all-items CPI).
If setobs and smpl are not specified in this way, the data frequency and sample range are set using the first variable read from the database.
If the series to be read are of higher frequency than the working dataset, you may specify a compaction method as below:
data LHUR PUNEW --compact=average
The five available compaction methods are "average" (takes the mean of the high frequency observations), "last" (uses the last observation), "first", "sum" and "spread". If no method is specified, the default is to use the average. The "spread" method is special: no information is lost, rather it is spread across multiple series, one per sub-period. So for example when adding a monthly series to a quarterly dataset three series are created, one for each month of the quarter; their names bear the suffixes m01, m02 and m03.
If the series to be read are of lower frequency than the working dataset the values of the added data are simply repeated as required, but note that the tdisagg function can then be used to distribution or interpolation ("temporal disaggregation").
In the case of native gretl databases (only), the "glob" characters * and ? can be used in varlist to import series that match the given pattern. For example, the following will import all series in the database whose names begin with cpi:
data cpi*
The --name option can be used to set a name for the imported series other than the original name in the database. The parameter must be a valid gretl identifier. This option is restricted to the case where a single series is specified for importation.
The --no-align option applies only to importation of series via ODBC. By default we require that the ODBC query returns information telling gretl on which rows of the dataset to place the incoming data—or at least that the number of incoming values matches either the length of the dataset or the length of the current sample range. Setting the --no-align option relaxes this requirement: failing the conditions just mentioned, incoming values are simply placed consecutively starting at the first row of the dataset. If there are fewer such values than rows in the dataset the trailing rows are filled with NAs; if there are more such values than rows the extra values are discarded. For more on ODBC importation see chapter 43 of the Gretl User's Guide.
Menu path: /File/Databases
| Arguments: | keyword parameters |
| Option: | --panel-time (see addobs below) |
| Examples: | dataset addobs 24 |
| dataset addobs 2 --panel-time | |
| dataset insobs 10 | |
| dataset compact 1 | |
| dataset compact 4 last | |
| dataset expand | |
| dataset transpose | |
| dataset sortby x1 | |
| dataset resample 500 | |
| dataset renumber x 4 | |
| dataset pad-daily 7 | |
| dataset unpad-daily | |
| dataset clear |
Performs various operations on the data set as a whole, depending on the given keyword, which must be addobs, insobs, clear, compact, expand, transpose, sortby, dsortby, resample, renumber, pad-daily or unpad-daily. Note: with the exception of clear, these actions are not available when the dataset is currently subsampled by selection of cases on some Boolean criterion.
addobs: Must be followed by a positive integer, call it n. Adds n extra observations to the end of the working dataset. This is primarily intended for forecasting purposes. The values of most variables over the additional range will be set to missing, but certain deterministic variables are recognized and extended, namely, a simple linear trend and periodic dummy variables. If the dataset takes the form of a panel, the default action is to add n cross-sectional units to the panel, but if the --panel-time flag is given the effect is to add n observations to the time series for each unit.
insobs: Must be followed by a positive integer no greater than the current number of observations. Inserts a single observation at the specified position. All subsequent data are shifted by one place and the dataset is extended by one observation. All variables apart from the constant are given missing values at the new observation. This action is not available for panel datasets.
clear: No parameter required. Clears out the current data, returning gretl to its initial "empty" state.
compact: This action is available for time series data only; it compacts all the series in the data set to a lower frequency. It requires one parameter, a positive integer representing the new frequency. In general this should be lower than the current frequency (for example, a value of 4 when the current frequency is 12 indicates compaction from monthly to quarterly). The one exception is a new frequency of 52 (weekly) when the current data are daily (frequency 5, 6 or 7). A second parameter may be given, namely one of sum, first, last or spread, to specify, respectively, compaction using the sum of the higher-frequency values, start-of-period values, end-of-period values, or spreading of the higher-frequency values across multiple series (one per sub-period). The default is to compact by averaging.
In the case of compaction from daily to weekly frequency (only), the two special options --repday and --weekstart are available. The first of these allows you to select a "representative day" of the week to serve as the weekly value. The parameter to this option must be an integer from 0 (Sunday) to 6 (Saturday). For example, giving --repday=3 selects Wednesday's value as the weekly value. If the --repday option is not given, we need to know on which day the week is deemed to start in order to align the data correctly. For 5- or 6-day data this is always taken to be Monday, but with 7-day data you have a choice between --weekstart=0 (Sunday) and --weekstart=1 (Monday), with Monday being the default.
expand: This action is only available for annual or quarterly time series data: annual data can be expanded to quarterly or monthly, and quarterly data to monthly. All series in the data set are padded out to the new frequency by repeating the existing values. If the original dataset is annual the default expansion is to quarterly but expand can be followed by 12 to request monthly. See the tdisagg function for more sophisticated means of converting data to higher frequency.
transpose: No additional parameter required. Transposes the current data set. That is, each observation (row) in the current data set will be treated as a variable (column), and each variable as an observation. This action may be useful if data have been read from some external source in which the rows of the data table represent variables.
sortby: The name of a single series or list is required. If one series is given, the observations on all variables in the dataset are re-ordered by increasing value of the specified series. If a list is given, the sort proceeds hierarchically: if the observations are tied in sort order with respect to the first key variable then the second key is used to break the tie, and so on until the tie is broken or the keys are exhausted. Note that this action is available only for undated data.
dsortby: Works as sortby except that the re-ordering is by decreasing value of the key series.
resample: Constructs a new dataset by random sampling, with replacement, of the rows of the current dataset. One argument is required, namely the number of rows to include. This may be less than, equal to, or greater than the number of observations in the original data. The original dataset can be retrieved via the command smpl full.
renumber: Requires the name of an existing series followed by an integer between 1 and the number of series in the dataset minus one. Moves the specified series to the specified position in the dataset, renumbering the other series accordingly. (Position 0 is occupied by the constant, which cannot be moved.)
pad-daily: Valid only if the current dataset contains dated daily data with an incomplete calendar. The effect is to pad the data out to a complete calendar by inserting blank rows (that is, rows containing nothing but NAs). This option requires an integer parameter, namely the number of days per week, which must be 5, 6 or 7, and must be greater than or equal to the current data frequency. On successful completion, the data calendar will be "complete" relative to this value. For example if days-per-week is 5 then all weekdays will be represented, whether or not any data are available for those days.
unpad-daily: Valid only if the current dataset contains dated daily data, in which case it performs the inverse operation of pad-daily. That is, any rows that contain nothing but NAs are removed, while the time-series property of the dataset is preserved along with the dates of the individual observations.
Menu path: /Data
| Variants: | delete varlist |
| delete varname | |
| delete --type=type-name | |
| delete pkgname | |
| Options: | --db (delete series from database) |
| --force (see below) |
This command is an all-purpose destructor. It should be used with caution; no confirmation is asked.
In the first form above, varlist is a list of series, given by name or ID number. Note that when you delete series any series with higher ID numbers than those on the deletion list will be re-numbered. If the --db option is given, this command deletes the listed series not from the current dataset but from a gretl database, assuming that a database has been opened, and the user has write permission for file in question. See also the open command.
In the second form, the name of a scalar, matrix, string or bundle may be given for deletion. The --db option is not applicable in this case. Note that series and variables of other types should not be mixed in a given call to delete.
In the third form, the --type option must be accompanied by one of the following type-names: matrix, bundle, string, list, scalar or array. The effect is to delete all variables of the given type. In this case no argument other than the option should be given.
The fourth form can be used to unload a function package. In this case the .gfn suffix must be supplied, as in
delete somepkg.gfn
Note that this does not delete the package file, it just unloads the package from memory.
In general it is not permitted to delete variables in the context of a loop, since this may threaten the integrity of the loop code. However, if you are confident that deleting a certain variable is safe you can override this prohibition by appending the --force flag to the delete command.
Menu path: Main window pop-up (single selection)
| Argument: | varlist |
| Examples: | penngrow.inp, sw_ch12.inp, sw_ch14.inp |
The first difference of each variable in varlist is obtained and the result stored in a new variable with the prefix d_. Thus diff x y creates the new variables
d_x = x(t) - x(t-1) d_y = y(t) - y(t-1)
Menu path: /Add/First differences of selected variables
| Variants: | difftest x y |
| difftest x --split-by=dummy | |
| Options: | --sign (Sign test, the default) |
| --rank-sum (Wilcoxon rank-sum test) | |
| --signed-rank (Wilcoxon signed-rank test) | |
| --verbose (print extra output) | |
| --quiet (suppress printed output) | |
| Examples: | ooballot.inp |
Carries out a nonparametric test for a difference between two samples, the specific test depending on the option selected. In the primary form the samples are represented by the series x and y. In the alternate form, with the --split-by option, the samples are two subsets of the series x, for which the series dummy takes the values 0 and 1, respectively. The alternate form is available only in conjunction with the --rank-sum option, since the other tests require paired observations.
With the --sign option, the Sign test is performed. This test is based on the fact that if two samples, x and y, are drawn randomly from the same distribution, the probability that xi > yi, for each observation i, should equal 0.5. The test statistic is w, the number of observations for which xi > yi. Under the null hypothesis this follows the Binomial distribution with parameters (n, 0.5), where n is the number of observations.
With the --rank-sum option, the Wilcoxon rank-sum test is performed. This test proceeds by ranking the observations from both samples jointly, from smallest to largest, then finding the sum of the ranks of the observations from one of the samples. The two samples do not have to be of the same size, and if they differ the smaller sample is used in calculating the rank-sum. Under the null hypothesis that the samples are drawn from populations with the same median, the probability distribution of the rank-sum can be computed for any given sample sizes; and for reasonably large samples a close Normal approximation exists.
With the --signed-rank option, the Wilcoxon signed-rank test is performed. This is designed for matched data pairs such as, for example, the values of a variable for a sample of individuals before and after some treatment. The test proceeds by finding the differences between the paired observations, xi – yi, ranking these differences by absolute value, then assigning to each pair a signed rank, the sign agreeing with the sign of the difference. One then calculates W+, the sum of the positive signed ranks. As with the rank-sum test, this statistic has a well-defined distribution under the null that the median difference is zero, which converges to the Normal for samples of reasonable size.
For the Wilcoxon tests, if the --verbose option is given then the ranking is printed. (This option has no effect if the Sign test is selected.)
On successful completion the accessors $test and $pvalue are available. If one just wants to obtain these values the --quiet flag can be appended to the command.
| Argument: | varlist |
| Option: | --reverse (mark variables as continuous) |
| Examples: | ooballot.inp, oprobit.inp |
Marks each variable in varlist as being discrete. By default all variables are treated as continuous; marking a variable as discrete affects the way the variable is handled in frequency plots, and also allows you to select the variable for the command dummify.
If the --reverse flag is given, the operation is reversed; that is, the variables in varlist are marked as being continuous.
Menu path: /Variable/Edit attributes
| Argument: | p ; depvar indepvars [ ; instruments ] |
| Options: | --quiet (don't show estimated model) |
| --vcv (print covariance matrix) | |
| --two-step (perform 2-step GMM estimation) | |
| --system (add equations in levels) | |
| --collapse (see below) | |
| --time-dummies (add time dummy variables) | |
| --dpdstyle (emulate DPD package for Ox) | |
| --asymptotic (uncorrected asymptotic standard errors) | |
| --keep-extra (see below) | |
| Examples: | dpanel 2 ; y x1 x2 |
| dpanel 2 ; y x1 x2 --system | |
| dpanel {2 3} ; y x1 x2 ; x1 | |
| dpanel 1 ; y x1 x2 ; x1 GMM(x2,2,3) | |
| See also bbond98.inp |
Carries out estimation of dynamic panel data models (that is, panel models including one or more lags of the dependent variable) using either the GMM-DIF or GMM-SYS method.
The parameter p represents the order of the autoregression for the dependent variable. In the simplest case this is a scalar value, but a pre-defined matrix may be given for this argument, to specify a set of (possibly non-contiguous) lags to be used.
The dependent variable and regressors should be given in levels form; they will be differenced automatically (since this estimator uses differencing to cancel out the individual effects).
The last (optional) field in the command is for specifying instruments. If no instruments are given, it is assumed that all the independent variables are strictly exogenous. If you specify any instruments, you should include in the list any strictly exogenous independent variables. For predetermined regressors, you can use the GMM function to include a specified range of lags in block-diagonal fashion. This is illustrated in the third example above. The first argument to GMM is the name of the variable in question, the second is the minimum lag to be used as an instrument, and the third is the maximum lag. The same syntax can be used with the GMMlevel function to specify GMM-type instruments for the equations in levels.
The --collapse option can be used to limit the proliferation of "GMM-style" instruments, which can be a problem with this estimator. Its effect is to reduce such instruments from one per lag per observation to one per lag.
By default the results of 1-step estimation are reported (with robust standard errors). You may select 2-step estimation as an option. In both cases tests for autocorrelation of orders 1 and 2 are provided, as well as Sargan and/or Hansen overidentification tests and a Wald test for the joint significance of the regressors. Note that in this differenced model first-order autocorrelation is not a threat to the validity of the model, but second-order autocorrelation violates the maintained statistical assumptions.
In the case of 2-step estimation, standard errors are by default computed using the finite-sample correction suggested by Windmeijer (2005). The standard asymptotic standard errors associated with the 2-step estimator are generally reckoned to be an unreliable guide to inference, but if for some reason you want to see them you can use the --asymptotic option to turn off the Windmeijer correction.
If the --time-dummies option is given, a set of time dummy variables is added to the specified regressors. The number of dummies is one less than the maximum number of periods used in estimation, to avoid perfect collinearity with the constant. The dummies are entered in differenced form unless the --dpdstyle option is given, in which case they are entered in levels.
As with other estimation commands, a $model bundle is available after estimation. In the case of dpanel, the --keep-extra option can be used to save additional information in this bundle, namely the GMM weight and instrument matrices.
For further details and examples, please see chapter 24 of the Gretl User's Guide.
Menu path: /Model/Panel/Dynamic panel model
| Argument: | varlist |
| Options: | --drop-first (omit lowest value from encoding) |
| --drop-last (omit highest value from encoding) |
For any suitable variables in varlist, creates a set of dummy variables coding for the distinct values of that variable. Suitable variables are those that have been explicitly marked as discrete, or those that take on a fairly small number of values all of which are "fairly round" (multiples of 0.25).
By default a dummy variable is added for each distinct value of the variable in question. For example if a discrete variable x has 5 distinct values, 5 dummy variables will be added to the data set, with names Dx_1, Dx_2 and so on. The first dummy variable will have value 1 for observations where x takes on its smallest value, 0 otherwise; the next dummy will have value 1 when x takes on its second-smallest value, and so on. If one of the option flags --drop-first or --drop-last is added, then either the lowest or the highest value of each variable is omitted from the encoding (which may be useful for avoiding the "dummy variable trap").
There is also a corresponding function for this command, see dummify. This makes it possible to embed the call directly in a regression specification. For example, the following line specifies a model where y is regressed on the set of dummy variables coding for x. (However, option flags are for the command variant only, not for the function variant of dummify.)
ols y dummify(x)Other access: Main window pop-up menu (single selection)
| Arguments: | depvar indepvars [ ; censvar ] |
| Options: | --exponential (use exponential distribution) |
| --loglogistic (use log-logistic distribution) | |
| --lognormal (use log-normal distribution) | |
| --medians (fitted values are medians) | |
| --robust (robust (QML) standard errors) | |
| --cluster=clustvar (see logit for explanation) | |
| --vcv (print covariance matrix) | |
| --verbose (print details of iterations) | |
| --quiet (don't print anything) | |
| Examples: | duration y 0 x1 x2 |
| duration y 0 x1 x2 ; cens | |
| See also weibull.inp |
Estimates a duration model: the dependent variable (which must be positive) represents the duration of some state of affairs, for example the length of spells of unemployment for a cross-section of respondents. By default the Weibull distribution is used but the exponential, log-logistic and log-normal distributions are also available.
If some of the duration measurements are right-censored (e.g. an individual's spell of unemployment has not come to an end within the period of observation) then you should supply the trailing argument censvar, a series in which non-zero values indicate right-censored cases.
By default the fitted values obtained via the accessor $yhat are the conditional means of the durations, but if the --medians option is given then $yhat provides the conditional medians instead.
Please see chapter 38 of the Gretl User's Guide for details.
Menu path: /Model/Limited dependent variable/Duration data
See if.
See if. Note that else requires a line to itself, before the following conditional command. You can append a comment, as in
else # OK, do something different
But you cannot append a command, as in
else x = 5 # wrong!
Ends a block of commands of some sort. For example, end system terminates an equation system.
See if.
Marks the end of a command loop. See loop.
| Options: | --complete (Create a complete document) |
| --output=filename (send output to specified file) |
Must follow the estimation of a model. Prints the estimated model in the form of a LaTeX equation. If a filename is specified using the --output option output goes to that file, otherwise it goes to a file with a name of the form equation_N.tex, where N is the number of models estimated to date in the current session. See also tabprint.
The output file will be written in the currently set workdir, unless the filename string contains a full path specification.
If the --complete flag is given, the LaTeX file is a complete document, ready for processing; otherwise it must be included in a document.
Menu path: Model window, /LaTeX
| Arguments: | depvar indepvars |
| Example: | equation y x1 x2 x3 const |
Specifies an equation within a system of equations (see system). The syntax for specifying an equation within an SUR system is the same as that for, e.g., ols. For an equation within a Three-Stage Least Squares system you may either (a) give an OLS-type equation specification and provide a common list of instruments using the instr keyword (again, see system), or (b) use the same equation syntax as for tsls.
| Arguments: | [ systemname ] [ estimator ] |
| Options: | --iterate (iterate to convergence) |
| --no-df-corr (no degrees of freedom correction) | |
| --geomean (see below) | |
| --quiet (don't print results) | |
| --verbose (print details of iterations) | |
| Examples: | estimate "Klein Model 1" method=fiml |
| estimate Sys1 method=sur | |
| estimate Sys1 method=sur --iterate |
Calls for estimation of a system of equations, which must have been previously defined using the system command. The name of the system should be given first, surrounded by double quotes if the name contains spaces. The estimator, which must be one of ols, tsls, sur, 3sls, fiml or liml, is preceded by the string method=. These arguments are optional if the system in question has already been estimated and occupies the place of the "last model"; in that case the estimator defaults to the previously used value.
If the system in question has had a set of restrictions applied (see the restrict command), estimation will be subject to the specified restrictions.
If the estimation method is sur or 3sls and the --iterate flag is given, the estimator will be iterated. In the case of SUR, if the procedure converges the results are maximum likelihood estimates. Iteration of three-stage least squares, however, does not in general converge on the full-information maximum likelihood results. The --iterate flag is ignored for other methods of estimation.
If the equation-by-equation estimators ols or tsls are chosen, the default is to apply a degrees of freedom correction when calculating standard errors. This can be suppressed using the --no-df-corr flag. This flag has no effect with the other estimators; no degrees of freedom correction is applied in any case.
By default, the formula used in calculating the elements of the cross-equation covariance matrix is
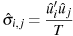
If the --geomean flag is given, a degrees of freedom correction is applied: the formula is
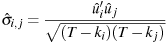
where the ks denote the number of independent parameters in each equation.
If the --verbose option is given and an iterative method is specified, details of the iterations are printed.
| Argument: | expression |
| Examples: | eval x |
| eval inv(X'X) | |
| eval sqrt($pi) |
This command makes gretl act like a glorified calculator. The program evaluates expression and prints its value. The argument may be the name of a variable, or something more complicated. In any case, it should be an expression which could stand as the right-hand side of an assignment statement.
In interactive use (for instance in the gretl console) an equals sign works as shorthand for eval, as in
=sqrt(x)
(with or without a space following "="). But this variant is not accepted in scripting mode since it could easily mask coding errors.
In most contexts print can be used in place of eval to much the same effect. See also printf for the case where you wish to combine textual and numerical output.
| Variants: | fcast [startobs endobs] [vname] |
| fcast [startobs endobs] steps-ahead [vname] --recursive | |
| Options: | --dynamic (create dynamic forecast) |
| --static (create static forecast) | |
| --out-of-sample (generate post-sample forecast) | |
| --no-stats (don't print forecast statistics) | |
| --stats-only (only print forecast statistics) | |
| --quiet (don't print anything) | |
| --recursive (see below) | |
| --all-probs (see below) | |
| --plot=filename (see below) | |
| Examples: | fcast 1997:1 2001:4 f1 |
| fcast fit2 | |
| fcast 2004:1 2008:3 4 rfcast --recursive | |
| See also gdp_midas.inp |
Must follow an estimation command. Forecasts are generated for a certain range of observations: if startobs and endobs are given, for that range (if possible); otherwise if the --out-of-sample option is given, for observations following the range over which the model was estimated; otherwise over the currently defined sample range. If an out-of-sample forecast is requested but no relevant observations are available, an error is flagged. Depending on the nature of the model, standard errors may also be generated; see below. Also see below for the special effect of the --recursive option.
If the last model estimated is a single equation, then the optional vname argument has the following effect: the forecast values are not printed, but are saved to the dataset under the given name. If the last model is a system of equations, vname has a different effect, namely selecting a particular endogenous variable for forecasting (the default being to produce forecasts for all the endogenous variables). In the system case, or if vname is not given, the forecast values can be retrieved using the accessor $fcast, and the standard errors, if available, via $fcse.
The choice between a static and a dynamic forecast applies only in the case of dynamic models, with an autoregressive error process or including one or more lagged values of the dependent variable as regressors. Static forecasts are one step ahead, based on realized values from the previous period, while dynamic forecasts employ the chain rule of forecasting. For example, if a forecast for y in 2008 requires as input a value of y for 2007, a static forecast is impossible without actual data for 2007. A dynamic forecast for 2008 is possible if a prior forecast can be substituted for y in 2007.
The default is to give a static forecast for any portion of the forecast range that lies within the sample range over which the model was estimated, and a dynamic forecast (if relevant) out of sample. The --dynamic option requests a dynamic forecast from the earliest possible date, and the --static option requests a static forecast even out of sample.
The --recursive option is presently available only for single-equation models estimated via OLS. When this option is given the forecasts are recursive. That is, each forecast is generated from an estimate of the given model using data from a fixed starting point (namely, the start of the sample range for the original estimation) up to the forecast date minus k, where k is the number of steps ahead, which must be given in the steps-ahead argument. The forecasts are always dynamic if this is applicable. Note that the steps-ahead argument should be given only in conjunction with the --recursive option.
When estimation is via ordered logit or probit, or multinomial logit, one may be interested in the estimated probabilities of each of the discrete outcomes rather than just a "most likely" outcome for each observation. This is supported by the --all-probs option: the output of fcast is then a matrix with one column per possible outcome. The vname argument can be used to name this matrix, in which case nothing is printed. If vname is not given the matrix can be retrieved via $fcast. The --plot option is incompatible with --all-probs.
The --plot option calls for a plot file to be produced, containing a graphical representation of the forecast. In the system case this option is available only when the vname argument is used to select a single variable for forecasting. The suffix of the filename argument to this option controls the format of the plot: .eps for EPS, .pdf for PDF, .png for PNG, .plt for a gnuplot command file. The dummy filename display can be used to force display of the plot in a window. For example,
fcast --plot=fc.pdf
will generate a graphic in PDF format. Absolute pathnames are respected, otherwise files are written to the gretl working directory.
The nature of the forecast standard errors (if available) depends on the nature of the model and the forecast. For static linear models standard errors are computed using the method outlined by Davidson and MacKinnon (2004); they incorporate both uncertainty due to the error process and parameter uncertainty (summarized in the covariance matrix of the parameter estimates). For dynamic models, forecast standard errors are computed only in the case of a dynamic forecast, and they do not incorporate parameter uncertainty. For nonlinear models, forecast standard errors are not presently available.
Menu path: Model window, /Analysis/Forecasts
This simple command (no arguments, no options) is intended for use in time-consuming scripts that may be executed via the gretl GUI (it is ignored by the command-line program), to give the user a visual indication that things are moving along and gretl is not "frozen".
Ordinarily if you launch a script in the GUI no output is shown until its execution is completed, but the effect of invoking flush is as follows:
On the first invocation, gretl opens a window, displays the output so far, and appends the message "Processing...".
On subsequent invocations the text shown in the output window is updated, and a new "processing" message is appended.
When execution of the script is completed any remaining output is automatically flushed to the text window.
Please note, there is no point in using flush in scripts that take less than (say) 5 seconds to execute. Also note that this command should not be used at a point in the script where there is no further output to be printed, as the "processing" message will then be misleading to the user.
The following illustrates the intended use of flush:
set echo off
scalar n = 10
loop i=1..n
# do some time-consuming operation
loop 100 --quiet
a = mnormal(200,200)
b = inv(a)
endloop
# print some results
printf "Iteration %2d done\n", i
if i < n
flush
endif
endloop
| Syntax: | foreign language=lang |
| Options: | --send-data[=list] (pre-load data; see below) |
| --quiet (suppress output from foreign program) |
This command opens a special mode in which commands to be executed by another program are accepted. You exit this mode with end foreign; at this point the stacked commands are executed.
At present the "foreign" programs supported in this way are GNU R (language=R), Python, Julia, GNU Octave (language=Octave), Jurgen Doornik's Ox and Stata. Language names are recognized on a case-insensitive basis.
In connection with R, Octave and Stata the --send-data option has the effect of making data from gretl's workspace available within the target program. By default the entire dataset is sent, but you can limit the data to be sent by giving the name of a predefined list of series. For example:
list Rlist = x1 x2 x3 foreign language=R --send-data=Rlist
See chapter 45 of the Gretl User's Guide for details and examples.
| Arguments: | series [ order ] |
| Options: | --gph (do Geweke and Porter-Hudak test) |
| --all (do both tests) | |
| --quiet (don't print results) |
Tests the specified series for fractional integration ("long memory"). The null hypothesis is that the integration order of the series is zero. By default the local Whittle estimator (Robinson, 1995) is used but if the --gph option is given the GPH test (Geweke and Porter-Hudak, 1983) is performed instead. If the --all flag is given then the results of both tests are printed.
For details on this sort of test, see Phillips and Shimotsu (2004).
If the optional order argument is not given the order for the test(s) is set automatically as the lesser of T/2 and T0.6.
The estimated fractional integration orders and their standard errors are available via the $result accessor. With the --all option, the Local Whittle estimate will be in the first row and the GPH estimate in the second one.
The results of the test can be retrieved using the accessors $test and $pvalue. These values are based on the Local Whittle Estimator unless the --gph option is given.
Menu path: /Variable/Unit root tests/Fractional integration
| Argument: | var |
| Options: | --nbins=n (specify number of bins) |
| --min=minval (specify minimum, see below) | |
| --binwidth=width (specify bin width, see below) | |
| --normal (test for the normal distribution) | |
| --gamma (test for gamma distribution) | |
| --silent (don't print anything) | |
| --matrix=name (use column of named matrix) | |
| --plot=mode-or-filename (see below) | |
| Examples: | freq x |
| freq x --normal | |
| freq x --nbins=5 | |
| freq x --min=0 --binwidth=0.10 |
With no options given, displays the frequency distribution for the series var (given by name or number) in tabular form, with the number of bins and their size chosen automatically, with or without an accompanying plot as explained below. Upon successful completion of the command, the frequency table can be retrieved as a matrix using the $result accessor.
If the --matrix option is given, var (which must be an integer) is instead interpreted as a 1-based index that selects a column from the named matrix. If the matrix in question is in fact a column vector, the var argument may be omitted.
By default the frequency distribution employs an automatically calculated number of bins if the data are continuous, or no binning if the data are discrete. To control this point you can (a) use the discrete command to set the status of var or (b), if the data are continuous, specify either the number of bins or the minimum value and the width of the bins, as shown in the last two examples above. The --min option sets the lower limit of the left-most bin.
If the --normal option is given, the Doornik–Hansen chi-square test for normality is computed. If the --gamma option is given, the test for normality is replaced by Locke's nonparametric test for the null hypothesis that the variable follows the gamma distribution; see Locke (1976), Shapiro and Chen (2001). Note that the parameterization of the gamma distribution used in gretl is (shape, scale).
By default, if gretl is not in batch mode a plot of the distribution is shown. This can be adjusted via the --plot option. The acceptable parameters to this option are none (to suppress the plot); display (to display a plot even when in batch mode); or a file name. The effect of providing a file name is as described for the --output option of the gnuplot command.
The --silent flag suppresses the usual text output. This might be used in conjunction with one or other of the distribution test options: the test statistic and its p-value are recorded, and can be retrieved using the accessors $test and $pvalue. It might also be used along with the --plot option if you just want a histogram and don't care to see the accompanying text.
Note that gretl does not have a function that matches this command, but it is possible to use the aggregate function to achieve the same purpose. In addition, the frequency distribution constructed by freq can be obtained in matrix form via the $result accessor.
Menu path: /Variable/Frequency distribution
| Argument: | [ message ] |
Applicable only in the context of a user-defined function (see function). Causes execution of the current function to terminate with an error condition flagged.
The optional message argument can take the form of a string literal or the name of a string variable; if present it is printed as part of the error message shown to the caller of the function.
See also the closely related function, errorif.
| Argument: | fnname |
Opens a block of statements in which a function is defined. This block must be closed with end function. (An exception is the case when a user-defined function shall be deleted, which is achieved by the single command line function foo delete for a function named "foo".) See chapter 14 of the Gretl User's Guide for details.
| Arguments: | p q ; depvar [ indepvars ] |
| Options: | --robust (robust standard errors) |
| --verbose (print details of iterations) | |
| --quiet (don't print anything) | |
| --vcv (print covariance matrix) | |
| --nc (do not include a constant) | |
| --stdresid (standardize the residuals) | |
| --fcp (use Fiorentini, Calzolari, Panattoni algorithm) | |
| --arma-init (initial variance parameters from ARMA) | |
| Examples: | garch 1 1 ; y |
| garch 1 1 ; y 0 x1 x2 --robust | |
| See also garch.inp, sw_ch14.inp |
Estimates a GARCH model (GARCH = Generalized Autoregressive Conditional Heteroskedasticity), either a univariate model or, if indepvars are specified, including the given exogenous variables. The integer values p and q (which may be given in numerical form or as the names of pre-existing scalar variables) represent the lag orders in the conditional variance equation:

The parameter p therefore represents the Generalized (or "AR") order, while q represents the regular ARCH (or "MA") order. If p is non-zero, q must also be non-zero otherwise the model is unidentified. However, you can estimate a regular ARCH model by setting q to a positive value and p to zero. The sum of p and q must be no greater than 5. Note that a constant is automatically included in the mean equation unless the --nc option is given.
By default native gretl code is used in estimation of GARCH models, but you also have the option of using the algorithm of Fiorentini, Calzolari and Panattoni (1996). The former uses the BFGS maximizer while the latter uses the information matrix to maximize the likelihood, with fine-tuning via the Hessian.
Several variant estimators of the covariance matrix are available with this command. By default, the Hessian is used unless the --robust option is given, in which case the QML (White) covariance matrix is used. Other possibilities (e.g. the information matrix, or the Bollerslev–Wooldridge estimator) can be specified via the garch_vcv keyword under the set command.
By default, the estimates of the variance parameters are initialized using the unconditional error variance from initial OLS estimation for the constant, and small positive values for the coefficients on the past values of the squared error and the error variance. The flag --arma-init calls for the starting values of these parameters to be set using an initial ARMA model, exploiting the relationship between GARCH and ARMA set out in Chapter 21 of Hamilton's Time Series Analysis. In some cases this may improve the chances of convergence.
The GARCH residuals and estimated conditional variance can be retrieved as $uhat and $h respectively. For example, to get the conditional variance:
series ht = $h
If the --stdresid option is given, the $uhat values are divided by the square root of ht.
Menu path: /Model/Univariate time series/GARCH
| Arguments: | newvar = formula |
NOTE: this command has undergone numerous changes and enhancements since the following help text was written, so for comprehensive and updated info on this command you'll want to refer to chapter 10 of the Gretl User's Guide. On the other hand, this help does not contain anything actually erroneous, so take the following as "you have this, plus more".
In the appropriate context, series, scalar, matrix, string, bundle and array are synonyms for this command.
Creates new variables, often via transformations of existing variables. See also diff, logs, lags, ldiff, sdiff and square for shortcuts. In the context of a genr formula, existing variables must be referenced by name, not ID number. The formula should be a well-formed combination of variable names, constants, operators and functions (described below). Note that further details on some aspects of this command can be found in chapter 10 of the Gretl User's Guide.
A genr command may yield either a series or a scalar result. For example, the formula x2 = x * 2 naturally yields a series if the variable x is a series and a scalar if x is a scalar. The formulae x = 0 and mx = mean(x) naturally return scalars. Under some circumstances you may want to have a scalar result expanded into a series or vector. You can do this by using series as an "alias" for the genr command. For example, series x = 0 produces a series all of whose values are set to 0. You can also use scalar as an alias for genr. It is not possible to coerce a vector result into a scalar, but use of this keyword indicates that the result should be a scalar: if it is not, an error occurs.
When a formula yields a series result, the range over which the result is written to the target variable depends on the current sample setting. It is possible, therefore, to define a series piecewise using the smpl command in conjunction with genr.
Supported arithmetical operators are, in order of precedence: ^ (exponentiation); *, / and % (modulus or remainder); + and -.
The available Boolean operators are (again, in order of precedence): ! (negation), && (logical AND), || (logical OR), >, <, == (is equal to), >= (greater than or equal), <= (less than or equal) and != (not equal). The Boolean operators can be used in constructing dummy variables: for instance (x > 10) returns 1 if x > 10, 0 otherwise.
Built-in constants are pi and NA. The latter is the missing value code: you can initialize a variable to the missing value with scalar x = NA.
The genr command supports a wide range of mathematical and statistical functions, including all the common ones plus several that are special to econometrics. In addition it offers access to numerous internal variables that are defined in the course of running regressions, doing hypothesis tests, and so on. For a listing of functions and accessors, see the Gretl Function Reference.
Besides the operators and functions noted above there are some special uses of genr:
genr time creates a time trend variable (1,2,3,...) called time. genr index does the same thing except that the variable is called index.
genr dummy creates dummy variables up to the periodicity of the data. In the case of quarterly data (periodicity 4), the program creates dq1 = 1 for first quarter and 0 in other quarters, dq2 = 1 for the second quarter and 0 in other quarters, and so on. With monthly data the dummies are named dm1, dm2, and so on; with daily data they are named dd1, dd2, and so on; and with other frequencies the names are dummy_1, dummy_2, etc.
genr unitdum and genr timedum create sets of special dummy variables for use with panel data. The first codes for the cross-sectional units and the second for the time period of the observations.
Note: In the command-line program, genr commands that retrieve model-related data always reference the model that was estimated most recently. This is also true in the GUI program, if one uses genr in the "gretl console" or enters a formula using the "Define new variable" option under the Add menu in the main window. With the GUI, however, you have the option of retrieving data from any model currently displayed in a window (whether or not it's the most recent model). You do this under the "Save" menu in the model's window.
The special variable obs serves as an index of the observations. For instance series dum = (obs==15) will generate a dummy variable that has value 1 for observation 15, 0 otherwise. You can also use this variable to pick out particular observations by date or name. For example, series d = (obs>1986:4), series d = (obs>"2008-04-01"), or series d = (obs=="CA"). If daily dates or observation labels are used in this context, they should be enclosed in double quotes. Quarterly and monthly dates (with a colon) may be used unquoted. Note that in the case of annual time series data, the year is not distinguishable syntactically from a plain integer; therefore if you wish to compare observations against obs by year you must use the function obsnum to convert the year to a 1-based index value, as in series d = (obs>obsnum(1986)).
Scalar values can be pulled from a series in the context of a genr formula, using the syntax varname[obs]. The obs value can be given by number or date. Examples: x[5], CPI[1996:01]. For daily data, the form YYYY-MM-DD should be used, e.g. ibm[1970-01-23].
An individual observation in a series can be modified via genr. To do this, a valid observation number or date, in square brackets, must be appended to the name of the variable on the left-hand side of the formula. For example, genr x[3] = 30 or genr x[1950:04] = 303.7.
Menu path: /Add/Define new variable
Other access: Main window pop-up menu| Arguments: | burnin N output |
| Options: | --keep (see below) |
| --quiet (suppress printing) | |
| --thinning (see below) | |
| Examples: | casella_ex1.inp |
This command is designed to facilitate the construction and execution of a Gibbs sampler, for a good explanation of which see Casella and George (1992). To summarize, the Gibbs sampler is a means of approximating the marginal distribution of one or more random variables which belong to a joint distribution, in case there's no analytical formula for the marginals, or if there is a formula it's excessively complicated. This is achieved by iterated simulation of the associated conditional distributions. Provided the marginals exist they can be approximated to arbitrary precision given a sufficient number of iterations.
The command takes the form of a block of statements that define scalar or matrix objects, started with gibbs and terminated by end gibbs. The structure is illustrated in the following simple example, where x follows the binomial distribution conditional on y, which in turn follows the beta distribution conditional on x, and it's the marginal distribution of x that is of interest.
gibbs burnin=500 N=5000 output=GB init y = randgen1(beta, a, n - b) record x = randgen1(b, y, n) y = randgen1(beta, x + a, n - x + b) end gibbs
On the first line a non-negative integer must be given for burnin and a positive integer for N (either numerical values or via the names of scalar variables). The burnin value determines the number of preliminary iterations, which are intended to stabilize the recursion and will not be recorded, while N gives the number of iterations to be recorded, in a bundle named by the output argument.
The interior lines of the block can have a keyword prepended, either init or record, with the following meanings.
init identifies a statement as an initializer, to be executed just once prior to the Gibbs iteration.
record tags a statement as one whose result should be recorded at each iteration.
Statements that feature neither keyword are taken to be part of the iteration but their results are not recorded in the output matrix. Statements tagged with init should be given first.
The primary content of the output bundle is a matrix named H which by default has N rows and a column dimension that depends on the number and type of the marginals to be recorded; matrix results are recorded in transposed vec form. Besides this matrix the bundle contains several items of metadata which make it a self-contained record of the sampler (see Sampler metadata below). If the bundle named in the output argument already exists it is overwritten, otherwise a new bundle is created.
Three options are supported; these should be appended to the terminating line of the block.
The --quiet flag suppresses the default printed output, which shows a brief progress report and some basic summary statistics pertaining to the output matrix.
By default, any variables newly created within the gibbs block are deleted once the iteration is completed. The effect of the --keep option is to preserve such variables, which may be useful for debugging a sampler.
The --thinning flag can be used to restrict the recording of results to a subset of the full number of iterations. For example --thinning=10 means that only every 10th iteration will be recorded. In that case the row dimension of the H matrix will be N/10 rather than N.
Extra members of the returned bundle record the burnin, N and thinning values. In addition it contains a sub-bundle pertaining to (and named for) each variable selected for recording. These sub-bundles hold
the starting column (startcol) and the number of columns (ncols) in the H matrix that are devoted to the variable in question;
a discrete boolean indicating whether the variable is discrete or not;
a type string (either scalar or matrix);
a matrix named stats which holds basic statistics.
| Options: | --two-step (two step estimation) |
| --iterate (iterated GMM) | |
| --vcv (print covariance matrix) | |
| --verbose (print details of iterations) | |
| --quiet (don't print anything) | |
| --lbfgs (use L-BFGS-B instead of regular BFGS) | |
| Examples: | hall_cbapm.inp |
Performs Generalized Method of Moments (GMM) estimation using the BFGS (Broyden, Fletcher, Goldfarb, Shanno) algorithm. You must specify one or more commands for updating the relevant quantities (typically GMM residuals), one or more sets of orthogonality conditions, an initial matrix of weights, and a listing of the parameters to be estimated, all enclosed between the tags gmm and end gmm. Any options should be appended to the end gmm line.
Please see chapter 27 of the Gretl User's Guide for details on this command. Here we just illustrate with a simple example.
gmm e = y - X*b orthog e ; W weights V params b end gmm
In the example above we assume that y and X are data matrices, b is an appropriately sized vector of parameter values, W is a matrix of instruments, and V is a suitable matrix of weights. The statement
orthog e ; W
indicates that the residual vector e is in principle orthogonal to each of the instruments composing the columns of W.
In estimating a nonlinear model it is often convenient to name the parameters tersely. In printing the results, however, it may be desirable to use more informative labels. This can be achieved via the additional keyword param_names within the command block. For a model with k parameters the argument following this keyword should be a double-quoted string literal holding k space-separated names, the name of a string variable that holds k such names, or the name of an array of k strings.
Menu path: /Model/Instrumental variables/GMM
| Variants: | gnuplot yvars xvar |
| gnuplot yvars --time-series | |
| gnuplot yvars xvar factor --factorized | |
| gnuplot yvar xvar zvars --control | |
| Options: | --with-lines[=varspec] (use lines, not points) |
| --with-lp[=varspec] (use lines and points) | |
| --with-impulses[=varspec] (use vertical lines) | |
| --with-boxes[=varspec] (use histograms) | |
| --with-steps[=varspec] (use perpendicular line segments) | |
| --time-series (plot against time) | |
| --single-yaxis (force use of just one y-axis) | |
| --y2axis=yvar (put specified variable on second y-axis) | |
| --ylogscale[=base] (use log scale for vertical axis) | |
| --control (see below) | |
| --factorized[=list] (see below) | |
| --fit=fitspec (see below) | |
| --font=fontspec (see below) | |
| --band=bundle (see below) | |
| --bands=array (see below) | |
| --matrix=name (plot columns of named matrix) | |
| --output=filename (send output to specified file) | |
| --outbuf=stringname (send output to specified string) | |
| --input=filename (take input from specified file) | |
| --inbuf=stringname (take input from specified string) | |
| Examples: | gnuplot y1 y2 x |
| gnuplot x --time-series --with-lines | |
| gnuplot wages educ gender --factorized | |
| gnuplot y x --fit=quadratic | |
| gnuplot y1 y2 x --with-lines=y2 |
The series in the list yvars are graphed against xvar. For a time series plot you may either give time as xvar or use the option flag --time-series. See also the plot and panplot commands.
By default, data-points are shown as points; this can be overridden by giving one of the options --with-lines, --with-lp (lines and points), --with-impulses or --with-steps. If more than one variable is to be plotted on the y axis, the effect of these options may be confined to a subset of the variables by using the varspec parameter. This should take the form of a comma-separated listing of the names or numbers of the variables to be plotted in the specified manner, or the name of a predefined list. For instance, the final example above shows how to plot y1 and y2 against x, such that y2 is represented by a line but y1 by points.
When yvars contains more than one variable it may be preferable to use two y axes (left and right). By default this is handled automatically, via a heuristic based on the relative scales of the variables, but two (mutually exclusive) options can be used to override the default: --single-yaxis prevents use of a second axis, while --y2axis=yvars specifies that one or more selected variables be plotted relative to a second axis. The yvars parameter can be the name of a single variable, the name of a list of variables, or two or more comma-separated variable names (with no spaces).
The --factorized option supports a X–Y plot in which the yvars are plotted in different styles (point type, color) depending on the value of a discrete factor variable at each observation. The factor must be specified following the x variable.
The simplest case features a single y variable and a 0/1 dummy variable as factor, as in the third usage example given above which plots wage against education, factorized by gender. But you can have more than one y variable and the factor may have more than two values. When multiple y variables are to be plotted you can restrict the factorization treatment to a subset by appending a parameter to the option flag: the name of a series or list of series. In the following example y and yhat are plotted against x, with factorization by id limited to y.
gnuplot y yhat x id --with-lines=yhat --factorized=y
When the --control option is specified three or more variables should be given: a single y variable, a single x variable, and one or more control variables, zvars. The effect is that y and x are each regressed on zvars and the y residuals are plotted against the x residuals. This plot shows the relationship between x and y taking into account the effect that the controls have on both.
You can specify the scale for the y axis as logarithmic rather than linear by using the --ylogscale option, together with a base parameter. For example,
gnuplot y x --ylogscale=2
plots the data such that the vertical axis is expressed as powers of 2. If the base is not specified it defaults to 10.
In the primary case the arguments yvars and xvar are required, and refer to series in the current dataset (given either by name or ID number). But if a named matrix is supplied via the --matrix option these arguments become optional: if the specified matrix has k columns, by default the first k – 1 columns are treated as the yvars and the last column as xvar. But if the --time-series option is given all k columns are plotted against time. If you wish to plot selected columns of the matrix, you should specify yvars and xvar in the form of 1-based column numbers. For example if you want a scatterplot of column 2 of matrix M against column 1, you can do:
gnuplot 2 1 --matrix=M
The --fit option is applicable only for bivariate scatterplots and single time-series plots. The default behavior for a scatterplot is to show the OLS fit if the slope coefficient is significant at the 10 percent level, while the default behavior for time-series is not to show any fitted line. You can call for different behavior by using this option along with one of the following fitspec parameter values. Note that if the plot is a single time series the place of x is taken by time.
linear: show the OLS fit regardless of its level of statistical significance.
none: don't show any fitted line.
inverse, quadratic, cubic, semilog or linlog: show a fitted line based on a regression of the specified type. By semilog, we mean a regression of log y on x; the fitted line represents the conditional expectation of y, obtained by exponentiation. By linlog we mean a regression of y on the log of x.
loess: show the fit from a robust locally weighted regression (also is sometimes known as "lowess").
The --band option can be used for plotting a "band" of some sort (typically representing a confidence interval) along with other data. Such a band is specified via a bundle, whose name is given as a parameter to the option. In the primary usage of this option the bundle has two required elements, to specify the center of the band (under the key center) and its width (under the key width). Each element must be given as either the quoted name of a series or (if the element in question happens to be constant) a numerical constant. In addition four optional elements are supported, as follows.
Under the key factor, a scalar giving a factor by which width should be multiplied (the default value being 1).
Under the key style, a string to specify how the band is represented, which must be one of line (the default) fill, dash, bars or step.
Under the key color, a color for the band, either as a string holding a gnuplot color name or as a hexadecimal RGB representation, given as a string or a scalar (see below for more details). By default the color is selected automatically.
Under the key title, a title for the band, to appear in the key or legend of the plot. By default bands are untitled.
Here are two examples of usage, employing the shorthand syntax _() for defining a bundle. The first just satisfies the minimum requirement while the second exercises all three options. We assume that y, x and w are all series in the current dataset.
bundle b1 = _(center="x", width="w") gnuplot y --time-series --with-lines --band=b1 bundle b2 = _(center="x", width="w", factor=1.96, style="fill") b2.color=0xcccccc b2.title = "95% interval" gnuplot y --time-series --with-lines --band=b2
If the plot is to contain two or more such bands, the option flag should be given in the plural and its parameter must be the name of an array of bundles, as in (following on from the example above):
bundles bb = defarray(b1, b2) gnuplot y --time-series --with-lines --bands=bb
When plotting matrix data rather than series, the only difference is that the center and width elements of the band bundle are replaced by a single element under the key bandmat. This should be a two-column matrix with the center of the band in the first column and the width in the second. Alternatively you can give a string under this key: the quoted name of a suitable matrix. This variant may be preferable if the matrix in question is to be reused with different factor values, since it avoids duplicating the matrix in memory.
An alternative usage of the --band option is to add "period bars" to a plot. By this we mean vertical bars occupying the full y-dimension of the plot and indicating the presence (bar) or absence (no bar) of some qualitative feature in a time-series plot. Such bars are commonly used to flag periods of recession; they could also be used to indicate periods of war, or anything that can be coded in a 0/1 dummy variable.
In this context the band bundle has a single required element: under the key dummy, the quoted name of a 0/1 series (or in the case of matrix data, the quoted name of a suitable column vector). The vertical bars will be "on" for observations where this series or vector has value 1 and "off" when it's 0. The center, width, factor and style keys are not applicable, but color can be used. Note that only one such specification can be used per plot. Here's an example:
open AWM17 --quiet
series dum = obs >= 1990:1 && obs <= 1994:2
bundle b = _(dummy="dum", color=0xcccccc)
gnuplot YER URX --with-lines --time-series \
--band=b --output=display {set key top left;}
Colors are identified via RGB numbers, usually expressed in 6-digit hexadecimal form: the first two digit indicate the amount of red (from 0 to 255), the middle ones the amount of green, and the last two the amount of blue. So for example 0xff0080 has maximum red, no green and some blue (it's a reddish purple). With gnuplot 5.2 onwards, you can use four digits instead of three: in this case, the first two digits indicate transparency, ranging from 0 (opaque) to 255 (transparent). For example, 0xc0ff0080 would give the color a value of 192 (c0 in hex) for transparency. You can check your gnuplot version by inspecting the $sysinfo bundle.
Hexadecimal colors can be passed either as scalars or as strings. A color string can be a quoted hexadecimal number (eg "0x191970"), but gnuplot recognizes some "shorthand" colors. For example, "violet" equates to "0xee82ee" and "brown" to "0xa52a2a". You can access the full list of color names recognized by gnuplot by issuing the command "show colornames" in gnuplot itself, or in the gretl console by doing
eval readfile("@gretldir/data/gnuplot/gpcolors.txt")
To achieve aesthetically pleasing results, you may want to use the rgbmix function.
In interactive mode the plot is displayed immediately. In batch mode (as when running a script) the default behavior is that a gnuplot command file is written in the user's working directory, with a name on the pattern gpttmpN.plt, starting with N = 01. The actual plots may be generated later using gnuplot (under MS Windows, wgnuplot). This behavior can be modified by use of the --output=filename option. This option controls the filename used, and at the same time allows you to specify a particular output format via the extension of the file name, as follows:
.eps: Encapsulated PostScript
.pdf: PDF
.png: PNG (Portable Network Graphics)
.emf: EMF (Microsoft's Enhanced MetaFile)
.html: HTML canvas
.svg: SVG (Scalable Vector Graphics)
.fig: Xfig (*nix drawing program)
.tex: pict2e (for use with LaTeX)
.tikz: TiKZ (for use with LaTeX).
If the dummy filename "display" is given then the plot is shown on screen as in interactive mode. If a filename with any extension other than those just mentioned is given, a gnuplot command file is written.
An alternative means of directing output is the --outbuf=stringname option. This writes gnuplot commands to the named string or "buffer". Note that --output and --outbuf are mutually incompatible.
The --font option can be used to specify a particular font for the plot. The fontspec parameter should take the form of the name of a font, optionally followed by a size in points separated from the name by a comma or space, all wrapped in double quotes, as in
--font="serif,12"
Note that the fonts available to gnuplot will vary by platform, and if you're writing a plot command that is intended to be portable it is best to restrict the font name to the generic sans or serif.
A further special option to this command is available: following the specification of the variables to be plotted and the option flag (if any), you may add literal gnuplot commands to control the appearance of the plot (for example, setting the plot title and/or the axis ranges). These commands should be enclosed in braces, and each gnuplot command must be terminated with a semicolon. A backslash may be used to continue a set of gnuplot commands over more than one line. Here is an example of the syntax:
{ set title 'My Title'; set yrange [0:1000]; }
Menu path: /View/Graph specified vars
Other access: Main window pop-up menu, graph button on toolbar| Variants: | graphpg add |
| graphpg fontscale value | |
| graphpg show | |
| graphpg free | |
| graphpg --output=filename |
The session "graph page" will work only if you have the LaTeX typesetting system installed, and are able to generate and view PDF or PostScript output.
In the session icon window, you can drag up to eight graphs onto the graph page icon. When you double-click on the graph page (or right-click and select "Display"), a page containing the selected graphs will be composed and opened in a suitable viewer. From there you should be able to print the page.
To clear the graph page, right-click on its icon and select "Clear".
Note that on systems other than MS Windows, you may have to adjust the setting for the program used to view PDF or PostScript files. Find that under the "Programs" tab in the gretl Preferences dialog box (under the Tools menu in the main window).
It's also possible to operate on the graph page via script, or using the console (in the GUI program). The following commands and options are supported:
To add a graph to the graph page, issue the command graphpg add after saving a named graph, as in
grf1 <- gnuplot Y X graphpg add
To display the graph page: graphpg show.
To clear the graph page: graphpg free.
To adjust the scale of the font used in the graph page, use graphpg fontscale scale, where scale is a multiplier (with a default of 1.0). Thus to make the font size 50 percent bigger than the default you can do
graphpg fontscale 1.5
To call for printing of the graph page to file, use the flag --output= plus a filename; the filename should have the suffix ".pdf", ".ps" or ".eps". For example:
graphpg --output="myfile.pdf"
The output file will be written in the currently set workdir, unless the filename string contains a full path specification.
In this context the output uses colored lines by default; to use dot/dash patterns instead of colors you can append the --monochrome flag.
| Argument: | plotspecs |
| Options: | --fontsize=fs (font size in points [10]) |
| --width=w (width of plot in pixels [800]) | |
| --height=h (height of plot in pixels [600]) | |
| --title=quoted string (add an overall title) | |
| --rows=r (see below) | |
| --cols=c (see below) | |
| --layout=lmat (see below) | |
| --output=destination (see below) | |
| --outbuf=alternative destination (see below) | |
| Examples: | gridplot myspecs --rows=3 --output=display |
| gridplot myspecs --layout=lmat --output=composite.pdf |
This command takes two or more individual plot specifications and arranges them in a grid to produce a composite plot. The single required argument, plotspecs, takes the form of an array of strings, each specifying a plot. The companion command gpbuild offers an easy way of creating such an array.
The shape of the grid can be set by any one of the three mutually incompatible options --rows, --cols and --layout. If no such option is given the number of rows is set to the square root of the number of plots (the size of the input array), rounded up to the nearest integer if necessary. Then the number of columns is set to the number of plots divided by the number of rows, again rounded up if necessary. The plots are placed in the grid by row, in their array order. If the --rows option is given this takes the place of the automatic setting, but the number of columns is set automatically as described above. If the --cols option is given instead, the number of rows is set automatically.
The --layout option, which requires a matrix parameter, offers a more flexible alternative. The matrix specifies the grid layout thus: 0 elements call for empty cells in the grid, and integer elements 1 to n refer to the subplots in their array order. So for example,
matrix m = {1,0,0; 2,3,0; 4,5,6}
gridplot ... --layout=m ...
calls for a lower-triangular layout of six plots in a 3 x 3 grid. Using this option one can omit some subplots, or even repeat some.
The --output option can be used to specify display (show the plot immediately) or the name of an output file. Alternatively --outbuf can be used to direct output, in the form of a gnuplot commands buffer, to a named string. In the absence of these options the output is an automatically named gnuplot command file. See gnuplot for details.
| Argument: | plotspecs |
| Example: | gpbuild MyPlots |
This command starts a block in which any commands or function calls which produce plots are treated specially, in order to produce an array of plot-specification strings for use with gridplot: the plotspecs argument supplies the name for this array. Such a block is terminated by the command "end gpbuild".
Within a gpbuild block only plotting commands get special treatment; all other commands are executed normally. There are just two restrictions to note.
Plotting commands should not include an output specification in this context, since that would conflict with the automatic redirection of output to the plotspecs array. An exception to this rule is allowed for --output=display (which is quite common as the default in plot-related function packages); this directive is silently ignored in favour of the automatic treatment.
Plots that invoke gnuplot's "multiplot" directive are not suitable for inclusion in a gpbuild block. That is because gridplot employs multiplot internally, and these constructs cannot be nested.
It is possible to prepare an array of plot specifications for use with gridplot without using a gpbuild block, as in the following example:
open data4-10 strings MyPlots = array(3) gnuplot ENROLL CATHOL --outbuf=MyPlots[1] gnuplot ENROLL INCOME --outbuf=MyPlots[2] gnuplot ENROLL COLLEGE --outbuf=MyPlots[3]
The above is essentially equivalent to
open data4-10 gpbuild MyPlots gnuplot ENROLL CATHOL gnuplot ENROLL INCOME gnuplot ENROLL COLLEGE end gpbuild
| Arguments: | depvar indepvars ; selection equation |
| Options: | --quiet (suppress printing of results) |
| --two-step (perform two-step estimation) | |
| --vcv (print covariance matrix) | |
| --opg (OPG standard errors) | |
| --robust (QML standard errors) | |
| --cluster=clustvar (see logit for explanation) | |
| --verbose (print extra output) | |
| Examples: | heckit y 0 x1 x2 ; ys 0 x3 x4 |
| See also heckit.inp |
Heckman-type selection model. In the specification, the list before the semicolon represents the outcome equation, and the second list represents the selection equation. The dependent variable in the selection equation (ys in the example above) must be a binary variable.
By default, the parameters are estimated by maximum likelihood. The covariance matrix of the parameters is computed using the negative inverse of the Hessian. If two-step estimation is desired, use the --two-step option. In this case, the covariance matrix of the parameters of the outcome equation is appropriately adjusted as per Heckman (1979).
Menu path: /Model/Limited dependent variable/Heckit
| Variants: | help |
| help functions | |
| help command | |
| help function | |
| Option: | --func (select functions help) |
If no arguments are given, prints a list of available commands. If the single argument functions is given, prints a list of available functions (see genr).
help command describes command (e.g. help smpl). help function describes function (e.g. help ldet). Some functions have the same names as related commands (e.g. diff): in that case the default is to print help for the command, but you can get help on the function by using the --func option.
Menu path: /Help
| Arguments: | hflist [ ; lflist ] |
| Options: | --with-lines (plot with lines) |
| --time-series (put time on x-axis) | |
| --output=filename (send output to specified file) |
Provides a means of plotting a high-frequency series, possibly along with one or more series observed at the base frequency of the dataset. The first argument should be a MIDAS list; the optional additional lflist terms, following a semicolon, should be regular ("low-frequency") series.
For details on the effect of the --output option, please see the gnuplot command.
| Arguments: | depvar indepvars |
| Options: | --no-squares (see below) |
| --vcv (print covariance matrix) | |
| --quiet (don't print anything) |
This command is applicable where heteroskedasticity is present in the form of an unknown function of the regressors which can be approximated by a quadratic relationship. In that context it offers the possibility of consistent standard errors and more efficient parameter estimates as compared with OLS.
The procedure involves (a) OLS estimation of the model of interest, followed by (b) an auxiliary regression to generate an estimate of the error variance, then finally (c) weighted least squares, using as weight the reciprocal of the estimated variance.
In the auxiliary regression (b) we regress the log of the squared residuals from the first OLS on the original regressors and their squares (by default), or just on the original regressors (if the --no-squares option is given). The log transformation is performed to ensure that the estimated variances are all non-negative. Call the fitted values from this regression u*. The weight series for the final WLS is then formed as 1/exp(u*).
Menu path: /Model/Other linear models/Heteroskedasticity corrected
| Argument: | series |
| Option: | --plot=mode-or-filename (see below) |
Calculates the Hurst exponent (a measure of persistence or long memory) for a time-series variable having at least 128 observations. The result (together with its standard error) can be retrieved via the $result accessor.
The Hurst exponent is discussed by Mandelbrot (1983). In theoretical terms it is the exponent, H, in the relationship
where RS is the "rescaled range" of the variable x in samples of size n and a is a constant. The rescaled range is the range (maximum minus minimum) of the cumulated value or partial sum of x over the sample period (after subtraction of the sample mean), divided by the sample standard deviation.
As a reference point, if x is white noise (zero mean, zero persistence) then the range of its cumulated "wandering" (which forms a random walk), scaled by the standard deviation, grows as the square root of the sample size, giving an expected Hurst exponent of 0.5. Values of the exponent significantly in excess of 0.5 indicate persistence, and values less than 0.5 indicate anti-persistence (negative autocorrelation). In principle the exponent is bounded by 0 and 1, although in finite samples it is possible to get an estimated exponent greater than 1.
In gretl, the exponent is estimated using binary sub-sampling: we start with the entire data range, then the two halves of the range, then the four quarters, and so on. For sample sizes smaller than the data range, the RS value is the mean across the available samples. The exponent is then estimated as the slope coefficient in a regression of the log of RS on the log of sample size.
By default, if gretl is not in batch mode a plot of the rescaled range is shown. This can be adjusted via the --plot option. The acceptable parameters to this option are none (to suppress the plot); display (to display a plot even when in batch mode); or a file name. The effect of providing a file name is as described for the --output option of the gnuplot command.
Menu path: /Variable/Hurst exponent
Flow control for command execution. Three sorts of construction are supported, as follows.
# simple form if condition commands endif # two branches if condition commands1 else commands2 endif # three or more branches if condition1 commands1 elif condition2 commands2 else commands3 endif
condition must be a Boolean expression, for the syntax of which see genr. More than one elif block may be included. In addition, if ... endif blocks may be nested.
| Argument: | filename |
| Option: | --force (force re-reading from file) |
| Examples: | include myfile.inp |
| include sols.gfn |
Intended for use in a command script, primarily for including definitions of functions. filename should have the extension inp (a plain-text script) or gfn (a gretl function package). The commands in filename are executed then control is returned to the main script.
The --force option is specific to gfn files: its effect is to force gretl to re-read the function package from file even if it is already loaded into memory. (Plain inp files are always read and processed in response to this command.)
See also run.
| Variants: | info |
| info --to-file=filename | |
| info --from-file=filename |
In its basic form, displays any supplementary information (metadata) stored with the current datafile. Otherwise, writes this information to file (with the --to-file option), or reads metadata from a specified file and attaches it to the current dataset (with --from-file, in which case the text should be valid UTF-8).
Menu path: /Data/Dataset info
| Arguments: | minvar maxvar indepvars |
| Options: | --quiet (suppress printing of results) |
| --verbose (print details of iterations) | |
| --robust (robust standard errors) | |
| --opg (see below) | |
| --cluster=clustvar (see logit for explanation) | |
| Examples: | intreg lo hi const x1 x2 |
| See also wtp.inp |
Estimates an interval regression model. This model arises when the dependent variable is imperfectly observed for some (possibly all) observations. In other words, the data generating process is assumed to be
y* = x b + ubut we only observe m <= y* <= M (the interval may be left- or right-unbounded). Note that for some observations m may equal M. The variables minvar and maxvar must contain NAs for left- and right-unbounded observations, respectively.
The model is estimated by maximum likelihood, assuming normality of the disturbance term.
By default, standard errors are computed using the negative inverse of the Hessian. If the --robust flag is given, then QML or Huber–White standard errors are calculated instead. In this case the estimated covariance matrix is a "sandwich" of the inverse of the estimated Hessian and the outer product of the gradient. Alternatively, the --opg option can be given, in which case standard errors are based on the outer product of the gradient alone.
Menu path: /Model/Limited dependent variable/Interval regression
| Arguments: | order ylist [ ; xlist ] [ ; rxlist ] |
| Options: | --nc (no constant) |
| --rc (restricted constant) | |
| --uc (unrestricted constant) | |
| --crt (constant and restricted trend) | |
| --ct (constant and unrestricted trend) | |
| --seasonals (include centered seasonal dummies) | |
| --asy (record asymptotic p-values) | |
| --quiet (print just the tests) | |
| --silent (don't print anything) | |
| --verbose (print details of auxiliary regressions) | |
| Examples: | johansen 2 y x |
| johansen 4 y x1 x2 --verbose | |
| johansen 3 y x1 x2 --rc | |
| See also hamilton.inp, denmark.inp |
Carries out the Johansen test for cointegration among the variables in ylist for the given lag order. For details of this test see chapter 33 of the Gretl User's Guide or Hamilton (1994), Chapter 20. P-values are computed via Doornik's gamma approximation (Doornik, 1998). Two sets of p-values are shown for the trace test, straight asymptotic values and values adjusted for the sample size. By default the $pvalue accessor gets the adjusted variant, but the --asy flag may be used to record the asymptotic values instead.
The inclusion of deterministic terms in the model is controlled by the option flags. The default if no option is specified is to include an "unrestricted constant", which allows for the presence of a non-zero intercept in the cointegrating relations as well as a trend in the levels of the endogenous variables. In the literature stemming from the work of Johansen (see for example his 1995 book) this is often referred to as "case 3". The first four options given above, which are mutually exclusive, produce cases 1, 2, 4 and 5 respectively. The meaning of these cases and the criteria for selecting a case are explained in chapter 33 of the Gretl User's Guide.
The optional lists xlist and rxlist allow you to control for specified exogenous variables: these enter the system either unrestrictedly (xlist) or restricted to the cointegration space (rxlist). These lists are separated from ylist and from each other by semicolons.
The --seasonals option, which may be combined with any of the other options, specifies the inclusion of a set of centered seasonal dummy variables. This option is available only for quarterly or monthly data.
The following table is offered as a guide to the interpretation of the results shown for the test, for the 3-variable case. H0 denotes the null hypothesis, H1 the alternative hypothesis, and c the number of cointegrating relations.
Rank Trace test Lmax test
H0 H1 H0 H1
---------------------------------------
0 c = 0 c = 3 c = 0 c = 1
1 c = 1 c = 3 c = 1 c = 2
2 c = 2 c = 3 c = 2 c = 3
---------------------------------------
See also the vecm command, and coint if you want the Engle–Granger cointegration test.
Menu path: /Model/Multivariate time series
| Arguments: | filename varname |
| Options: | --data=column-name (see below) |
| --filter=expression (see below) | |
| --ikey=inner-key (see below) | |
| --okey=outer-key (see below) | |
| --aggr=method (see below) | |
| --tkey=column-name,format-string (see below) | |
| --verbose (report on progress) |
This command imports one or more data series from the source filename (which must be either a delimited text data file or a "native" gretl data file) under the name varname. For details please see chapter 7 of the Gretl User's Guide; here we just give a brief summary of the available options. See also append for simpler joining operations.
The --data option can be used to specify the column heading of the data in the source file, if this differs from the name by which the data should be known in gretl.
The --filter option can be used to specify a criterion for filtering the source data (that is, selecting a subset of observations).
The --ikey and --okey options can be used to specify a mapping between observations in the current dataset and observations in the source data (for example, individuals can be matched against the household to which they belong).
The --aggr option is used when the mapping between observations in the current dataset and the source is not one-to-one.
The --tkey option is applicable only when the current dataset has a time-series structure. It can be used to specify the name of a column containing dates to be matched to the dataset and/or the format in which dates are represented in that column.
The join command can handle the importation of several series at once. This happens when (a) the varname argument is a space-separated list of names rather than a single name, or (b) when it points to an array of strings: the elements of this array should be the names of the series to import.
This methods has some limitations, however: the --data option is not available. When importing multiple series you are obliged to accept their "outer" names. The other options apply uniformly to all the series imported via a given command.
| Argument: | y |
| Options: | --alt (use Epanechnikov kernel) |
| --scale=s (scale factor for bandwidth) | |
| --output=filename (send plot to specified file) |
Plots a kernel density estimate for the series y. By default the kernel is Gaussian but if the --alt flag is given the Epanechnikov kernel is used. The degree of smoothing can be adjusted via the --scale option, which has a default value of 1.0 (higher values of s produce a smoother result).
The option --output has the effect of sending the output to the specified file; use "display" to force output to the screen. See the gnuplot command for more detail on this option.
For a more flexible means of generating kernel density estimates, with the option of retrieving the result as a matrix, see the kdensity function.
Menu path: /Variable/Estimated density plot
| Arguments: | order varlist |
| Options: | --trend (include a trend) |
| --seasonals (include seasonal dummies) | |
| --verbose (print regression results) | |
| --quiet (suppress printing of results) | |
| --difference (use first difference of variable) | |
| Examples: | kpss 8 y |
| kpss 4 x1 --trend |
For use of this command with panel data please see the final section in this entry.
Computes the KPSS test (Kwiatkowski et al, Journal of Econometrics, 1992) for stationarity, for each of the specified variables (or their first difference, if the --difference option is selected). The null hypothesis is that the variable in question is stationary, either around a level or, if the --trend option is given, around a deterministic linear trend.
The order argument determines the size of the window used for Bartlett smoothing. If a negative value is given this is taken as a signal to use an automatic window size of 4(T/100)0.25, where T is the sample size.
If the --verbose option is chosen the results of the auxiliary regression are printed, along with the estimated variance of the random walk component of the variable.
The critical values shown for the test statistic are based on response surfaces estimated in the manner set out by Sephton (Economics Letters, 1995), which are more accurate for small samples than the values given in the original KPSS article. When the test statistic lies between the 10 percent and 1 percent critical values a p-value is shown; this is obtained by linear interpolation and should not be taken too literally. See the kpsscrit function for a means of obtaining these critical values programmatically.
When the kpss command is used with panel data, to produce a panel unit root test, the applicable options and the results shown are somewhat different. While you may give a list of variables for testing in the regular time-series case, with panel data only one variable may be tested per command. And the --verbose option has a different meaning: it produces a brief account of the test for each individual time series (the default being to show only the overall result).
When possible, the overall test (null hypothesis: the series in question is stationary for all the panel units) is calculated using the method of Choi (Journal of International Money and Finance, 2001). This is not always straightforward, the difficulty being that while the Choi test is based on the p-values of the tests on the individual series, we do not currently have a means of calculating p-values for the KPSS test statistic; we must rely on a few critical values.
If the test statistic for a given series falls between the 10 percent and 1 percent critical values, we are able to interpolate a p-value. But if the test falls short of the 10 percent value, or exceeds the 1 percent value, we cannot interpolate and can at best place a bound on the global Choi test. If the individual test statistic falls short of the 10 percent value for some units but exceeds the 1 percent value for others, we cannot even compute a bound for the global test.
Menu path: /Variable/Unit root tests/KPSS test
| Variants: | labels [ varlist ] |
| labels --to-file=filename | |
| labels --from-file=filename | |
| labels --delete | |
| Examples: | oprobit.inp |
In the first form, prints out the informative labels (if present) for the series in varlist, or for all series in the dataset if varlist is not specified.
With the option --to-file, writes to the named file the labels for all series in the dataset, one per line. If no labels are present an error is flagged; if some series have labels and others do not, a blank line is printed for series with no label. The output file will be written in the currently set workdir, unless the filename string contains a full path specification.
With the option --from-file, reads the specified file (which should be plain text) and assigns labels to the series in the dataset, reading one label per line and taking blank lines to indicate blank labels.
The --delete option does what you'd expect: it removes all the series labels from the dataset.
Menu path: /Data/Variable labels
| Arguments: | depvar indepvars |
| Options: | --vcv (print covariance matrix) |
| --no-vcv (don't compute covariance matrix) | |
| --quiet (don't print anything) |
Calculates a regression that minimizes the sum of the absolute deviations of the observed from the fitted values of the dependent variable. Coefficient estimates are derived using the Barrodale–Roberts simplex algorithm; a warning is printed if the solution is not unique.
Standard errors are derived using the bootstrap procedure with 500 drawings. The covariance matrix for the parameter estimates, printed when the --vcv flag is given, is based on the same bootstrap. Since this is quite an expensive operation, the --no-vcv option is provided for the case where the covariance matrix is not required; when this option is given standard errors will not be available.
Note that this method can be slow when the sample is large or there are many regressors; in that case it may be preferable to use the quantreg command. Given a dependent variable y and a list of regressors X, the following commands are basically equivalent, except that the quantreg method uses the faster Frisch–Newton algorithm and provides analytical rather than bootstrapped standard errors.
lad y const X quantreg 0.5 y const X
Menu path: /Model/Robust estimation/Least Absolute Deviation
| Arguments: | [ order ; ] varlist |
| Option: | --bylag (order terms by lag) |
| Examples: | lags x y |
| lags 12 ; x y | |
| lags 4 ; x1 x2 x3 --bylag | |
| See also sw_ch12.inp, sw_ch14.inp |
Creates new series which are lagged values of each of the series in varlist. By default the number of lags created equals the periodicity of the data. For example, if the periodicity is 4 (quarterly), the command lags x creates
x_1 = x(t-1) x_2 = x(t-2) x_3 = x(t-3) x_4 = x(t-4)
The number of lags created can be controlled by the optional first parameter (which, if present, must be followed by a semicolon).
The --bylag option is meaningful only if varlist contains more than one series and the maximum lag order is greater than 1. By default the lagged terms are added to the dataset by variable: first all lags of the first series, then all lags of the second series, and so on. But if --bylag is given, the ordering is by lags: first lag 1 of all the listed series, then lag 2 of all the list series, and so on.
This facility is also available as a function: see lags.
Menu path: /Add/Lags of selected variables
| Argument: | varlist |
The first difference of the natural log of each series in varlist is obtained and the result stored in a new series with the prefix ld_. Thus ldiff x y creates the new variables
ld_x = log(x) - log(x(-1)) ld_y = log(y) - log(y(-1))
Menu path: /Add/Log differences of selected variables
| Options: | --save (save the resulting series) |
| --overwrite (OK to overwrite existing series) | |
| --quiet (don't print results) | |
| --plot=mode-or-filename (see below) | |
| Examples: | leverage.inp |
Must follow an ols command. Calculates the leverage (h, which must lie in the range 0 to 1) for each data point in the sample on which the previous model was estimated. Displays the residual (u) for each observation along with its leverage and a measure of its influence on the estimates, uh/(1 – h). "Leverage points" for which the value of h exceeds 2k/n (where k is the number of parameters being estimated and n is the sample size) are flagged with an asterisk. For details on the concepts of leverage and influence see Davidson and MacKinnon (1993), Chapter 2.
DFFITS values are also computed: these are Studentized residuals (residuals divided by their standard errors) multiplied by the square root of h(1 – h). They give a measure of the difference in fit for observation i depending on whether or not that observation is included in the sample for estimation. For more on this point see chapter 12 of Maddala's Introduction to Econometrics or Belsley, Kuh and Welsch (1980). For more on Studentized residuals see the section headed Accessor matrix below.
If the --save flag is given with this command, the leverage, influence and DFFITS values are added to the current data set; in this context the --quiet flag may be used to suppress the printing of results. The default names of the saved series are, respectively, lever, influ and dffits. If series of these names already exist, what happens depends on whether the --overwrite option is given. If so, the existing series are overwritten; if not, the names will be adjusted to ensure uniqueness. In the latter case the newly generated series will always be the highest-numbered three series in the dataset.
After execution, the $test accessor returns the cross-validation criterion, which is defined as the sum of squared deviations of the dependent variable from its forecast value, the forecast for each observation being based on a sample from which that observation is excluded. (This is known as the leave-one-out estimator). For a broader discussion of the cross-validation criterion, see Davidson and MacKinnon's Econometric Theory and Methods, pages 685–686, and the references therein.
By default, if this command is invoked interactively a plot of the leverage and influence values is shown. This can be adjusted via the --plot option. The acceptable parameters to this option are none (to suppress the plot); display (to display a plot even when in script mode); or a file name. The effect of providing a file name is as described for the --output option of the gnuplot command.
Besides the --save option noted above, results from this command can be retrieved in the form of a three-column matrix via the $result accessor. The first two columns of this matrix contain leverage and influence values (as with --save) but the third column holds Studentized residuals rather than DFFITS values. These are "externally Studentized" or "jackknifed" residuals—that is, the standard error in the divisor for observation i uses the residual mean square with that observation omitted. Such a residual can be interpreted as a t statistic for the hypothesis that a 0/1 dummy variable coding specifically for observation i would have a true coefficient of zero. For further discussion of Studentized residuals see Chatterjee and Hadi (1986).
DFFITS values may be obtained from the $result matrix as follows:
R = $result dffits = R[,3] .* sqrt(R[,1] ./ (1-R[,1]))
Or using series:
series h = $result[,1] # leverage series sr = $result[,3] # Studentized residual series dffits = sr * sqrt(h/(1-h))
Menu path: Model window, /Analysis/Influential observations
| Arguments: | order series |
| Options: | --nc (test without a constant) |
| --ct (with constant and trend) | |
| --quiet (suppress printing of results) | |
| --verbose (print per-unit results) | |
| Examples: | levinlin 0 y |
| levinlin 2 y --ct | |
| levinlin {2,2,3,3,4,4} y |
Carries out the panel unit-root test described by Levin, Lin and Chu (2002). The null hypothesis is that all of the individual time series exhibit a unit root, and the alternative is that none of the series has a unit root. (That is, a common AR(1) coefficient is assumed, although in other respects the statistical properties of the series are allowed to vary across individuals.)
By default the test ADF regressions include a constant; to suppress the constant use the --nc option, or to add a linear trend use the --ct option. (See the adf command for explanation of ADF regressions.)
The (non-negative) order for the test (governing the number of lags of the dependent variable to include in the ADF regressions) may be given in either of two forms. If a scalar value is given, this is applied to all the individuals in the panel. The alternative is to provide a matrix containing a specific lag order for each individual; this must be a vector with as many elements as there are individuals in the current sample range. Such a matrix can be specified by name, or constructed using braces as illustrated in the last example above.
When the --verbose option is given, the following results are printed for each unit in the panel: delta, the coefficient on the lagged level in each ADF regression; s2e, the estimated variance of the innovations; and s2y, the estimated long-run variance of the differenced series.
Note that panel unit-root tests can also be conducted using the adf and kpss commands.
Menu path: /Variable/Unit root tests/Levin-Lin-Chu test
| Arguments: | depvar indepvars |
| Options: | --ymax=value (specify maximum of dependent variable) |
| --robust (robust standard errors) | |
| --cluster=clustvar (see logit for explanation) | |
| --vcv (print covariance matrix) | |
| --fixed-effects (see below) | |
| --quiet (don't print anything) | |
| Examples: | logistic y const x |
| logistic y const x --ymax=50 |
Logistic regression: carries out an OLS regression using the logistic transformation of the dependent variable,
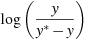
In the case of panel data the specification may include individual fixed effects.
The dependent variable must be strictly positive. If all its values lie between 0 and 1, the default is to use a y* value (the asymptotic maximum of the dependent variable) of 1; if its values lie between 0 and 100, the default y* is 100.
If you wish to set a different maximum, use the --ymax option. Note that the supplied value must be greater than all of the observed values of the dependent variable.
The fitted values and residuals from the regression are automatically adjusted using the inverse of the logistic transformation:
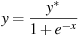
where x represents either a fitted value or a residual from the OLS regression using the logistic dependent variable. The reported values are therefore comparable with the original dependent variable. The need for approximation arises because the inverse transformation is nonlinear and therefore does not conserve expectation.
The --fixed-effects option is applicable only if the dataset takes the form of a panel. In that case we subtract the group means from the logistic transform of the dependent variable and estimation proceeds as usual for fixed effects.
Note that if the dependent variable is binary, you should use the logit command instead.
Menu path: /Model/Limited dependent variable/Logistic
Menu path: /Model/Panel/FE logistic
| Arguments: | depvar indepvars |
| Options: | --robust (robust standard errors) |
| --cluster=clustvar (clustered standard errors) | |
| --multinomial (estimate multinomial logit) | |
| --vcv (print covariance matrix) | |
| --verbose (print details of iterations) | |
| --quiet (don't print results) | |
| --p-values (show p-values instead of slopes) | |
| --estrella (select pseudo-R-squared variant) | |
| Examples: | keane.inp, oprobit.inp |
If the dependent variable is a binary variable (all values are 0 or 1) maximum likelihood estimates of the coefficients on indepvars are obtained via the Newton–Raphson method. As the model is nonlinear the slopes depend on the values of the independent variables. By default the slopes with respect to each of the independent variables are calculated (at the means of those variables) and these slopes replace the usual p-values in the regression output. This behavior can be suppressed by giving the --p-values option. The chi-square statistic tests the null hypothesis that all coefficients are zero apart from the constant.
By default, standard errors are computed using the negative inverse of the Hessian. If the --robust flag is given, then QML or Huber–White standard errors are calculated instead. In this case the estimated covariance matrix is a "sandwich" of the inverse of the estimated Hessian and the outer product of the gradient; see chapter 10 of Davidson and MacKinnon (2004). But if the --cluster option is given, then "cluster-robust" standard errors are produced; see chapter 22 of the Gretl User's Guide for details.
By default the pseudo-R-squared statistic suggested by McFadden (1974) is shown, but in the binary case if the --estrella option is given, the variant recommended by Estrella (1998) is shown instead. This variant arguably mimics more closely the properties of the regular R2 in the context of least-squares estimation.
If the dependent variable is binary, logit coefficients represent the log of the odds ratio (the ratio of the probability of y = 1 to that of y = 0). In this case the $model bundle available after estimation includes an the extra element named oddsratios, a matrix with four columns holding the exponentiated coefficient (odds ratio) plus standard error computed via the delta method and 95 percent confidence interval, for each regressor. Note, however, that the confidence interval is calculated as the exponential of that for the original coefficient.
If the dependent variable is not binary but is discrete, then by default it is interpreted as an ordinal response, and Ordered Logit estimates are obtained. However, if the --multinomial option is given, the dependent variable is interpreted as an unordered response, and Multinomial Logit estimates are produced. (In either case, if the variable selected as dependent is not discrete an error is flagged.) The accessor $allprobs is available after estimation, to get a matrix containing the estimated probabilities of the outcomes at each observation (observations in rows, outcomes in columns).
If you want to use logit for analysis of proportions (where the dependent variable is the proportion of cases having a certain characteristic, at each observation, rather than a 1 or 0 variable indicating whether the characteristic is present or not) you should not use the logit command, but rather construct the logit variable, as in
series lgt_p = log(p/(1 - p))
and use this as the dependent variable in an OLS regression. See chapter 12 of Ramanathan (2002).
Menu path: /Model/Limited dependent variable/Logit
| Argument: | varlist |
The natural log of each of the series in varlist is obtained and the result stored in a new series with the prefix l_ ("el" underscore). For example, logs x y creates the new variables l_x = ln(x) and l_y = ln(y).
Menu path: /Add/Logs of selected variables
| Argument: | control |
| Options: | --progressive (enable special forms of certain commands) |
| --verbose (echo commands and show confirmatory messages) | |
| --decr (see below) | |
| Examples: | loop 1000 |
| loop i=1..10 | |
| loop while essdiff > .00001 | |
| loop for (r=-.99; r<=.99; r+=.01) | |
| loop foreach i xlist | |
| See also armaloop.inp, keane.inp |
This command opens a special mode in which the program accepts commands to be executed repeatedly. You exit the mode of entering loop commands with endloop: at this point the stacked commands are executed.
The parameter control may take any of five forms, as shown in the examples: an integer number of times to repeat the commands within the loop; a range of integer values for an index variable; "while" plus a boolean condition; "for" plus three expressions in parentheses, separated by semicolons (which emulates the for statement in the C programming language); or "foreach" plus an index variable and a list.
The --decr option is specific to the "range of integer values" form of loop. By default the index is incremented by 1 at each iteration, and if the starting value is less than the ending value the loop will not run at all. When --decr is given the index is decremented by 1 at each iteration.
See chapter 13 of the Gretl User's Guide for full details and examples. The effect of the --progressive option (which is designed for use in Monte Carlo simulations) is explained there. Not all gretl commands may be used within a loop; the commands available in this context are also set out there.
By default, execution of commands proceeds more quietly within loops than in other contexts. If you want more feedback on what's going on in a loop, give the --verbose option.
| Argument: | varlist |
| Options: | --quiet (don't print anything) |
| --save (add distances to the dataset) | |
| --vcv (print covariance matrix) |
Computes the Mahalanobis distances of each observation from the centroid, using the series in varlist. The Mahalanobis distance is the distance between two points in a k-dimensional space, scaled by the statistical variation in each dimension of the space. For example, if p and q are two observations on a set of k variables with covariance matrix C, then the Mahalanobis distance between the observations is given by
where (p – q) is a k-vector. This reduces to Euclidean distance if the covariance matrix is the identity matrix.
The space for which distances are computed is defined by the selected variables. For each observation in the current sample range, the distance is computed between the observation and the centroid of the selected variables. This distance is the multidimensional counterpart of a standard z-score, and can be used to judge whether a given observation "belongs" with a group of other observations.
If the --vcv option is given, the covariance matrix and its inverse are printed. If the --save option is given, the distances are saved to the dataset under the name mdist (or mdist1, mdist2 and so on if there is already a variable of that name).
See also the distance function.
Menu path: /View/Mahalanobis distances
| Argument: | filename |
| Options: | --index (write auxiliary index file) |
| --translations (write auxiliary strings file) | |
| --quiet (operate quietly) |
Supports creation of a gretl function package via the command line. The mode of operation of this command depends on the extension of filename, which must be either .gfn or .zip.
Writes a gfn file. It is assumed that a package specification file, with the same basename as filename but with the extension .spec, is accessible, along with any auxiliary files that it references. It is also assumed that all the functions to be packaged have been read into memory.
Writes a zip package file (gfn plus other materials). If a gfn file of the same basename as filename is found, gretl checks for corresponding inp and spec files: if these are both found and at least one of them is newer than the gfn file then the gfn is rebuilt, otherwise the existing gfn is used. If no such file is found, gretl first attempts to build the gfn.
The option flags support the writing of auxiliary files, intended for use with gretl "addons". The index file is a short XML document containing basic information about the package; it has the same basename as the package and the extension .xml. The translations file contains strings from the package that may be suitable for translation, in C format; for package foo this file is named foo-i18n.c. These files are not produced if the command is operating in zip mode and a pre-existing gfn file is used.
For details on all of this, see the gretl Function Package Guide.
Menu path: /File/Function packages/New package
| Variants: | markers --to-file=filename |
| markers --from-file=filename | |
| markers --to-array=name | |
| markers --from-array=name | |
| markers --from-series=name | |
| markers --delete |
The options --to-file and --to-array provide means of saving the observation marker strings from the current dataset, either to a named file or a named array. If no such strings are present an error is flagged. In the file case output will be written in the current workdir unless the filename string contains a full path specification. The markers are written one per line. In the array case, if name is the identifier of an existing array of strings it will be overwritten, otherwise a new array will be created.
With the option --from-file, reads the specified file (which should be UTF-8 text) and assigns observation markers to the rows in the dataset, reading one marker per line. In general there should be at least as many markers in the file as observations in the dataset, but if the dataset is a panel it is also acceptable if the number of markers in the file matches the number of cross-sectional units (in which case the markers are repeated for each time period.) The --from-array option works similarly, reading from a named array of strings.
The option --from-series offers a convenient way of creating observation markers by copying from a string-valued series. An error is flagged if the specified series does not have string values.
The --delete option does what you'd expect: it removes the observation marker strings from the dataset.
Menu path: /Data/Observation markers
| Variants: | meantest x y |
| meantest x --split-by=dummy | |
| Options: | --unequal-vars (assume variances are unequal) |
| --paired (conduct a paired test) | |
| --quiet (suppress printed output) | |
| --robust (time series only) | |
| Examples: | meantest x y |
| meantest x y --unequal-vars | |
| meantest x y --paired | |
| meantest x --split-by=d |
In its primary usage, calculates the t statistic for the null hypothesis that the population means are equal for the series x and y, and shows output including the p-value. Results can be retrieved using the accessors $test and $pvalue, in which case the --quiet option may used to omit the printout.
In its alternate form, with the --split-by option, the samples whose means are tested for equality are two subsets of the series x, for which the series dummy takes the values 0 and 1, respectively. The alternate form is not compatible with the --paired option.
By default the test statistic is calculated on the assumption that the variances are equal for the two variables. With the --unequal-vars option the variances are assumed to be different; in this case the degrees of freedom for the test statistic are approximated as per Satterthwaite (1946).
In the primary case (only) the --paired option can be given, to test the null hypothesis that the mean difference between the paired values of the two series arguments is zero. Otherwise, pairing is not assumed.
Given time series data, in the primary case (only) the --robust option can be given to conduct a test of equality of the means of x and y which is robust in respect of serial correlation.
Menu path: /Tools/Test statistic calculator
| Arguments: | depvar indepvars ; MIDAS-terms |
| Options: | --vcv (print covariance matrix) |
| --robust (robust standard errors) | |
| --quiet (suppress printing of results) | |
| --levenberg (see below) | |
| Examples: | midasreg y 0 y(-1) ; mds(X, 1, 9, 1, theta) |
| midasreg y 0 y(-1) ; mds(X, 1, 9, 0) | |
| midasreg y 0 y(-1) ; mdsl(XL, 2, theta) | |
| See also gdp_midas.inp |
Carries out least-squares estimation (either NLS or OLS, depending on the specification) of a MIDAS (Mixed Data Sampling) model. Such models include one or more independent variables that are observed at a higher frequency than the dependent variable; for a good brief introduction see Armesto, Engemann and Owyang (2010).
The variables in indepvars should be of the same frequency as the dependent variable. This list should usually include const or 0 (intercept) and typically includes one or more lags of the dependent variable. The high-frequency terms are given after a semicolon; each one takes the form of a number of comma-separated arguments within parentheses, prefixed by either mds or mdsl.
mds: this variant generally requires 5 arguments, as follows: the name of a MIDAS list, two integers giving the minimum and maximum high-frequency lags, an integer between 0 and 4 (or string, see below) specifying the type of parameterization to use, and the name of a vector holding initial values of the parameters. The example below calls for lags 3 to 11 of the high-frequency series represented by the list X, using parameterization type 1 (exponential Almon, see below) with initializer theta.
mds(X, 3, 11, 1, theta)
mdsl: generally requires 3 arguments: the name of a list of MIDAS lags, an integer (or string, see below) to specify the type of parameterization and the name of an initialization vector. In this case the minimum and maximum lags are implicit in the initial list argument. In the example below Xlags should be a list which already holds all the required lags; such a list can be constructed using the hflags function.
mdsl(XLags, 1, theta)
The supported types of parameterization are shown below; in the context of mds and mdsl specifications these may be given in the form of numeric codes or the double-quoted strings shown after the numbers.
0 or "umidas": unrestricted MIDAS or U-MIDAS (each lag has its own coefficient)
1 or "nealmon": normalized exponential Almon; requires at least one parameter, commonly uses two
2 or "beta0": normalized beta with a zero last lag; requires exactly two parameters
3 or "betan": normalized beta with non-zero last lag; requires exactly three parameters
4 or "almonp": (non-normalized) Almon polynomial; requires at least one parameter
5 or "beta1": as beta0, but with the first parameter fixed at 1, leaving a single free parameter.
When the parameterization is U-MIDAS, the final initializer argument is not required. In other cases you can request an automatic initialization by substituting one or other of these two forms for the name of an initial parameter vector:
The keyword null: this is accepted if the parameterization has a fixed number of terms (the beta cases, with 2 or 3 parameters). It's also accepted for the exponential Almon case, implying the default of 2 parameters.
An integer value giving the required number of parameters.
The estimation method used by this command depends on the specification of the high-frequency terms. In the case of U-MIDAS the method is OLS, otherwise it is nonlinear least squares (NLS). When the normalized exponential Almon or normalized beta parameterization is specified, the default NLS method is a combination of constrained BFGS and OLS, but the --levenberg option can be given to force use of the Levenberg–Marquardt algorithm.
Menu path: /Model/Univariate time series/MIDAS
| Arguments: | log-likelihood function [ derivatives ] |
| Options: | --quiet (don't show estimated model) |
| --vcv (print covariance matrix) | |
| --hessian (base covariance matrix on the Hessian) | |
| --robust[=hac] (QML or HAC covariance matrix) | |
| --cluster=clustvar (cluster-robust covariance matrix) | |
| --verbose (print details of iterations) | |
| --no-gradient-check (see below) | |
| --auxiliary (see below) | |
| --lbfgs (use L-BFGS-B instead of regular BFGS) | |
| Examples: | weibull.inp, biprobit_via_ghk.inp, frontier.inp, keane.inp |
Performs Maximum Likelihood (ML) estimation using either the BFGS (Broyden, Fletcher, Goldfarb, Shanno) algorithm or Newton's method. The user must specify the log-likelihood function. The parameters of this function must be declared and given starting values prior to estimation. Optionally, the user may specify the derivatives of the log-likelihood function with respect to each of the parameters; if analytical derivatives are not supplied, a numerical approximation is computed.
This help text assumes use of the default BFGS maximizer. For information on using Newton's method please see chapter 26 of the Gretl User's Guide.
Simple example: Suppose we have a series X with values 0 or 1 and we wish to obtain the maximum likelihood estimate of the probability, p, that X = 1. (In this simple case we can guess in advance that the ML estimate of p will simply equal the proportion of Xs equal to 1 in the sample.)
The parameter p must first be added to the dataset and given an initial value. For example, scalar p = 0.5.
We then construct the MLE command block:
mle loglik = X*log(p) + (1-X)*log(1-p) deriv p = X/p - (1-X)/(1-p) end mle
The first line above specifies the log-likelihood function. It starts with the keyword mle, then a dependent variable is specified and an expression for the log-likelihood is given (using the same syntax as in the genr command). The next line (which is optional) starts with the keyword deriv and supplies the derivative of the log-likelihood function with respect to the parameter p. If no derivatives are given, you should include a statement using the keyword params which identifies the free parameters: these are listed on one line, separated by spaces and can be either scalars, or vectors, or any combination of the two. For example, the above could be changed to:
mle loglik = X*log(p) + (1-X)*log(1-p) params p end mle
in which case numerical derivatives would be used.
Note that any option flags should be appended to the ending line of the MLE block. For example:
mle loglik = X*log(p) + (1-X)*log(1-p) params p end mle --quiet
If the log-likelihood function returns a series or vector giving per-observation values then estimated standard errors are by default based on the Outer Product of the Gradient (OPG), while if the --hessian option is given they are instead based on the negative inverse of the Hessian, which is approximated numerically. If the --robust option is given, a QML estimator is used (namely, a sandwich of the negative inverse of the Hessian and the OPG). If the hac parameter is added to this option the OPG is augmented in the manner of Newey and West to allow for serial correlation of the gradient. (This only makes sense with time-series data.) However, if the log-likelihood function just returns a scalar value, the OPG is not available (and so neither is the QML estimator), and standard errors are of necessity computed using the numerical Hessian.
In the event that you just want the primary parameter estimates you can give the --auxiliary option, which suppresses computation of the covariance matrix and standard errors; this will save some CPU cycles and memory usage.
If you supply analytical derivatives, by default gretl runs a numerical check on their plausibility. Occasionally this may produce false positives, instances where correct derivatives appear to be wrong and estimation is refused. To counter this, or to achieve a little extra speed, you can give the option --no-gradient-check. Obviously, you should do this only if you are confident that the gradient you have specified is right.
In estimating a nonlinear model it is often convenient to name the parameters tersely. In printing the results, however, it may be desirable to use more informative labels. This can be achieved via the additional keyword param_names within the command block. For a model with k parameters the argument following this keyword should be a double-quoted string literal holding k space-separated names, the name of a string variable that holds k such names, or the name of an array of k strings.
For an in-depth description of mle please refer to chapter 26 of the Gretl User's Guide.
Menu path: /Model/Maximum likelihood
| Variants: | modeltab add |
| modeltab show | |
| modeltab free | |
| modeltab --output=filename | |
| modeltab --options=bundle |
Manipulates the gretl "model table". See chapter 3 of the Gretl User's Guide for details. The sub-commands have the following effects: add adds the last model estimated to the model table, if possible; show displays the model table in a window; and free clears the table.
To call for printing of the model table, use the flag --output= plus a filename. If the filename has the suffix ".tex", the output will be in TeX format; if the suffix is ".rtf" the output will be RTF; otherwise it will be plain text. In the case of TeX output the default is to produce a "fragment", suitable for inclusion in a document; if you want a stand-alone document instead, use the --complete option, for example
modeltab --output="myfile.tex" --complete
The --options= flag, which requires the name of a gretl bundle, can be used to control certain aspects of the formatting of the model table. The following keys are recognized:
colheads: integer from 1 to 4, selects from the four supported column-head styles: Arabic numbering, Roman numbering, alphabetical, or using the names under which models have been saved. The default is 1 (Arabic numbering).
tstats: boolean, replace standard errors with t-statistics or not (default 0).
pvalues: boolean, include P-values or not (default 0).
asterisks: boolean, show significance-level asterisks or not (default 1).
digits: integer from 2 to 6, selects the number of significant digits shown (default 4).
decplaces: integer from 2 to 6, selects the number of decimal places shown.
Note that the last two keys are mutually exclusive. They offer alternative ways of specifying the precision to which numerical values are shown: either in terms of significant digits or decimal places. The default is 4 significant digits.
An options bundle can be supplied via a stand-alone command (as in the last of the examples above) or it can be combined with the show action or --output option. For example, the following script builds a simple model table and displays it, with P-values shown instead of significance asterisks:
open data9-7 ols 1 0 2 3 4 modeltab add ols 1 0 2 3 modeltab add bundle myopts = _(pvalues=1, asterisks=0) modeltab show --options=myopts
Menu path: Session icon window, Model table icon
| Arguments: | coeffmat names [ addstats ] |
| Option: | --output=filename (send output to specified file) |
Prints the coefficient table and optional additional statistics for a model estimated "by hand". Mainly useful for user-written functions.
The argument coeffmat should be a k by 2 matrix containing k coefficients and k associated standard errors. The names argument should supply at least k names for labeling the coefficients; it can take the form of a string literal (in double quotes) or string variable, in which case the names should be separated by commas or spaces, or it may be given as a named array of strings.
The optional argument addstats is a vector containing p additional statistics to be printed under the coefficient table. If this argument is given, then names should contain k + p names, the additional p names to be associated with the extra statistics.
If addstats is not provided and the coeffmat matrix has row names attached, then the names argument can be omitted.
To put the output into a file, use the flag --output= plus a filename. If the filename has the suffix ".tex", the output will be in TeX format; if the suffix is ".rtf" the output will be RTF; otherwise it will be plain text. In the case of TeX output the default is to produce a "fragment", suitable for inclusion in a document; if you want a stand-alone document instead, use the --complete option.
The output file will be written in the currently set workdir, unless the filename string contains a full path specification.
| Argument: | [ order ] |
| Options: | --normality (normality of residual) |
| --logs (nonlinearity, logs) | |
| --squares (nonlinearity, squares) | |
| --autocorr (serial correlation) | |
| --arch (ARCH) | |
| --white (heteroskedasticity, White's test) | |
| --white-nocross (White's test, squares only) | |
| --breusch-pagan (heteroskedasticity, Breusch–Pagan) | |
| --robust (robust variance estimate for Breusch–Pagan) | |
| --panel (heteroskedasticity, groupwise) | |
| --comfac (common factor restriction, AR1 models only) | |
| --xdepend (cross-sectional dependence, panel data only) | |
| --quiet (don't print details) | |
| --silent (don't print anything) | |
| Examples: | credscore.inp |
Must immediately follow an estimation command. The discussion below applies to usage of the command following estimation of a single-equation model; see chapter 32 of the Gretl User's Guide for an account of how modtest operates after estimation of a VAR.
Depending on the option given, this command carries out one of the following: the Doornik–Hansen test for the normality of the error term; a Lagrange Multiplier test for nonlinearity (logs or squares); White's test (with or without cross-products) or the Breusch–Pagan test (Breusch and Pagan, 1979) for heteroskedasticity; the LMF test for serial correlation (Kiviet, 1986); a test for ARCH (Autoregressive Conditional Heteroskedasticity; see also the arch command); a test of the common factor restriction implied by AR(1) estimation; or a test for cross-sectional dependence in panel-data models. With the exception of the normality, common factor and cross-sectional dependence tests most of the options are only available for models estimated via OLS, but see below for details regarding two-stage least squares.
The optional order argument is relevant only in case the --autocorr or --arch options are selected. The default is to run these tests using a lag order equal to the periodicity of the data, but this can be adjusted by supplying a specific lag order.
The --robust option applies only when the Breusch–Pagan test is selected; its effect is to use the robust variance estimator proposed by Koenker (1981), making the test less sensitive to the assumption of normality.
The --panel option is available only when the model is estimated on panel data: in this case a test for groupwise heteroskedasticity is performed (that is, for a differing error variance across the cross-sectional units).
The --comfac option is available only when the model is estimated via an AR(1) method such as Hildreth–Lu. The auxiliary regression takes the form of a relatively unrestricted dynamic model, which is used to test the common factor restriction implicit in the AR(1) specification.
The --xdepend option is available only for models estimated on panel data. The test statistic is that developed by Pesaran (2004). The null hypothesis is that the error term is independently distributed across the cross-sectional units or individuals.
By default, the program prints the auxiliary regression on which the test statistic is based, where applicable. This may be suppressed by using the --quiet flag (minimal printed output) or the --silent flag (no printed output). The test statistic and its p-value may be retrieved using the accessors $test and $pvalue respectively.
When a model has been estimated by two-stage least squares (see tsls), the LM principle breaks down and gretl offers some equivalents: the --autocorr option computes Godfrey's test for autocorrelation (Godfrey, 1994) while the --white option yields the HET1 heteroskedasticity test (Pesaran and Taylor, 1999).
For additional diagnostic tests on models, see chow, cusum, reset and qlrtest.
Menu path: Model window, /Tests
| Argument: | see below |
The mpi command starts a block of statements (which must be ended with end mpi) to be executed using MPI (Message Passing Interface) parallelization. See gretl-mpi.pdf for a full account of this facility.
| Arguments: | depvar indepvars |
| Options: | --vcv (print covariance matrix) |
| --simple-print (do not print auxiliary statistics) | |
| --quiet (suppress printing of results) |
Computes OLS estimates for the specified model using multiple precision floating-point arithmetic, with the help of the Gnu Multiple Precision (GMP) library. By default 256 bits of precision are used for the calculations, but this can be increased via the environment variable GRETL_MP_BITS. For example, when using the bash shell one could issue the following command, before starting gretl, to set a precision of 1024 bits.
export GRETL_MP_BITS=1024
A rather arcane option is available for this command (primarily for testing purposes): if the indepvars list is followed by a semicolon and a further list of numbers, those numbers are taken as powers of x to be added to the regression, where x is the last variable in indepvars. These additional terms are computed and stored in multiple precision. In the following example y is regressed on x and the second, third and fourth powers of x:
mpols y 0 x ; 2 3 4
Menu path: /Model/Other linear models/High precision OLS
| Arguments: | depvar indepvars [ ; offset ] |
| Options: | --model1 (use NegBin 1 model) |
| --robust (QML covariance matrix) | |
| --cluster=clustvar (see logit for explanation) | |
| --opg (see below) | |
| --vcv (print covariance matrix) | |
| --verbose (print details of iterations) | |
| --quiet (don't print results) | |
| Examples: | camtriv.inp |
Estimates a Negative Binomial model. The dependent variable is taken to represent a count of the occurrence of events of some sort, and must have only non-negative integer values. By default the model NegBin 2 is used, in which the conditional variance of the count is given by μ(1 + αμ), where μ denotes the conditional mean. But if the --model1 option is given the conditional variance is μ(1 + α).
The optional offset series works in the same way as for the poisson command. The Poisson model is a restricted form of the Negative Binomial in which α = 0 by construction.
By default, standard errors are computed using a numerical approximation to the Hessian at convergence. But if the --opg option is given the covariance matrix is based on the Outer Product of the Gradient (OPG), or if the --robust option is given QML standard errors are calculated, using a "sandwich" of the inverse of the Hessian and the OPG.
Menu path: /Model/Limited dependent variable/Count data
| Arguments: | function [ derivatives ] |
| Options: | --quiet (don't show estimated model) |
| --robust (robust standard errors) | |
| --vcv (print covariance matrix) | |
| --verbose (print details of iterations) | |
| --no-gradient-check (see below) | |
| Examples: | wg_nls.inp, ects_nls.inp |
Performs Nonlinear Least Squares (NLS) estimation using a modified version of the Levenberg–Marquardt algorithm. You must supply a function specification. The parameters of this function must be declared and given starting values prior to estimation. Optionally, you may specify the derivatives of the regression function with respect to each of the parameters. If you do not supply derivatives you should instead give a list of the parameters to be estimated (separated by spaces or commas), preceded by the keyword params. In the latter case a numerical approximation to the Jacobian is computed.
It is easiest to show what is required by example. The following is a complete script to estimate the nonlinear consumption function set out in William Greene's Econometric Analysis (Chapter 11 of the 4th edition, or Chapter 9 of the 5th). The numbers to the left of the lines are for reference and are not part of the commands. Note that any option flags, such as --vcv for printing the covariance matrix of the parameter estimates, should be appended to the final command, end nls.
1 open greene11_3.gdt 2 ols C 0 Y 3 scalar a = $coeff(0) 4 scalar b = $coeff(Y) 5 scalar g = 1.0 6 nls C = a + b * Y^g 7 deriv a = 1 8 deriv b = Y^g 9 deriv g = b * Y^g * log(Y) 10 end nls --vcv
It is often convenient to initialize the parameters by reference to a related linear model; that is accomplished here on lines 2 to 5. The parameters alpha, beta and gamma could be set to any initial values (not necessarily based on a model estimated with OLS), although convergence of the NLS procedure is not guaranteed for an arbitrary starting point.
The actual NLS commands occupy lines 6 to 10. On line 6 the nls command is given: a dependent variable is specified, followed by an equals sign, followed by a function specification. The syntax for the expression on the right is the same as that for the genr command. The next three lines specify the derivatives of the regression function with respect to each of the parameters in turn. Each line begins with the keyword deriv, gives the name of a parameter, an equals sign, and an expression whereby the derivative can be calculated. As an alternative to supplying analytical derivatives, you could substitute the following for lines 7 to 9:
params a b g
Line 10, end nls, completes the command and calls for estimation. Any options should be appended to this line.
If you supply analytical derivatives, by default gretl runs a numerical check on their plausibility. Occasionally this may produce false positives, instances where correct derivatives appear to be wrong and estimation is refused. To counter this, or to achieve a little extra speed, you can give the option --no-gradient-check. Obviously, you should do this only if you are confident that the gradient you have specified is right.
In estimating a nonlinear model it is often convenient to name the parameters tersely. In printing the results, however, it may be desirable to use more informative labels. This can be achieved via the additional keyword param_names within the command block. For a model with k parameters the argument following this keyword should be a double-quoted string literal holding k space-separated names, the name of a string variable that holds k such names, or the name of an array of k strings.
For further details on NLS estimation please see chapter 25 of the Gretl User's Guide.
Menu path: /Model/Nonlinear Least Squares
| Argument: | series |
| Options: | --dhansen (Doornik–Hansen test, the default) |
| --swilk (Shapiro–Wilk test) | |
| --lillie (Lilliefors test) | |
| --jbera (Jarque–Bera test) | |
| --all (do all tests) | |
| --quiet (suppress printed output) |
Carries out a test for normality for the given series. The specific test is controlled by the option flags (but if no flag is given, the Doornik–Hansen test is performed). Note: the Doornik–Hansen and Shapiro–Wilk tests are recommended over the others, on account of their superior small-sample properties.
The test statistic and its p-value may be retrieved using the accessors $test and $pvalue. Please note that if the --all option is given, the result recorded is that from the Doornik–Hansen test.
Menu path: /Variable/Normality test
| Argument: | series_length |
| Option: | --preserve (preserve variables other than series) |
| Example: | nulldata 500 |
Establishes a "blank" data set, containing only a constant and an index variable, with periodicity 1 and the specified number of observations. This may be used for simulation purposes: functions such as uniform() and normal() will generate artificial series from scratch to fill out the data set. This command may be useful in conjunction with loop. See also the "seed" option to the set command.
By default, this command cleans out all data in gretl's current workspace: not only series but also matrices, scalars, strings, etc. If you give the --preserve option, however, any currently defined variables other than series are retained.
Menu path: /File/New data set
| Arguments: | depvar indepvars |
| Options: | --vcv (print covariance matrix) |
| --robust (robust standard errors) | |
| --cluster=clustvar (clustered standard errors) | |
| --jackknife (see below) | |
| --simple-print (do not print auxiliary statistics) | |
| --quiet (suppress printing of results) | |
| --anova (print an ANOVA table) | |
| --no-df-corr (suppress degrees of freedom correction) | |
| --print-final (see below) | |
| Examples: | ols 1 0 2 4 6 7 |
| ols y 0 x1 x2 x3 --vcv | |
| ols y 0 x1 x2 x3 --quiet |
Computes ordinary least squares (OLS) estimates with depvar as the dependent variable and indepvars as the list of independent variables. Variables may be specified by name or number; use the number zero for a constant term.
Besides coefficient estimates and standard errors, the program also prints p-values for t (two-tailed) and F-statistics. A p-value below 0.01 indicates statistical significance at the 1 percent level and is marked with ***. ** indicates significance between 1 and 5 percent and * indicates significance between the 5 and 10 percent levels. Model selection statistics (the Akaike Information Criterion or AIC and Schwarz's Bayesian Information Criterion) are also printed. The formula used for the AIC is that given by Akaike (1974), namely minus two times the maximized log-likelihood plus two times the number of parameters estimated.
If the option --no-df-corr is given, the usual degrees of freedom correction is not applied when calculating the estimated error variance (and hence also the standard errors of the parameter estimates).
The option --print-final is applicable only in the context of a loop. It arranges for the regression to be run silently on all but the final iteration of the loop. See chapter 13 of the Gretl User's Guide for details.
Various internal variables may be retrieved following estimation. For example
series uh = $uhat
saves the residuals under the name uh. See the "accessors" section of the gretl function reference for details.
The specific formula ("HC" version) used for generating robust standard errors when the --robust option is given can be adjusted via the set command. The --jackknife option has the effect of selecting an hc_version of 3a. The --cluster overrides the selection of HC version, and produces robust standard errors by grouping the observations by the distinct values of clustvar; see chapter 22 of the Gretl User's Guide for details.
Menu path: /Model/Ordinary Least Squares
Other access: Beta-hat button on toolbar| Argument: | varlist |
| Options: | --test-only (don't replace the current model) |
| --chi-square (give chi-square form of Wald test) | |
| --quiet (print only the basic test result) | |
| --silent (don't print anything) | |
| --vcv (print covariance matrix for reduced model) | |
| --auto[=criterion] (sequential elimination, see below) | |
| Examples: | omit 5 7 9 |
| omit seasonals --quiet | |
| omit --auto=BIC | |
| omit --auto=0.05 | |
| See also restrict.inp, sw_ch12.inp, sw_ch14.inp |
This command must follow an estimation command. In its primary form, it calculates a Wald test for the joint significance of the variables in varlist, which should be a subset (though not necessarily a proper subset) of the independent variables in the model last estimated. The results of the test may be retrieved using the accessors $test and $pvalue.
Unless the restriction removes all the original regressors, by default the restricted model is estimated and it replaces the original as the "current model" for the purposes of, for example, retrieving the residuals as $uhat or doing further tests. This behavior may be suppressed via the --test-only option.
By default the F-form of the Wald test is recorded; the --chi-square option may be used to record the chi-square form instead.
If the restricted model is both estimated and printed, the --vcv option has the effect of printing its covariance matrix, otherwise this option is ignored.
The --auto option (which cannot be combined with --test-only) calls for backward stepwise regression. In this case varlist is optional; if it is given then only the listed variables are taken to be candidates for omission; otherwise all the regressors are candidates. At each step the method determines which candidate might best be eliminated according to the specified criterion (given as parameter to the option). The algorithm halts when no further improvement is possible. The criterion must take one of the following forms:
An Information Criterion: AIC, BIC or HQC. The "best" candidate at each step is then that whose omission gives the greatest improvement (reduction) in the selected criterion—until there is no candidate whose omission gives an improvement, when the algorithm halts.
An α value (positive decimal fraction). In this case the regressor with the greatest two-sided P-value is chosen for omission—until there is no candidate whose P-value is greater than α, when the algorithm halts.
If no criterion is specified with the --auto option, the default is to use the P-value method with α = 0.10.
Menu path: Model window, /Tests/Omit variables
| Argument: | filename |
| Options: | --quiet (don't print list of series) |
| --preserve (preserve variables other than series) | |
| --select=selection (read only the specified series, see below) | |
| --frompkg=pkgname (see below) | |
| --all-cols (see below) | |
| --www (use a database on the gretl server) | |
| --odbc (use an ODBC database) | |
| See below for additional specialized options | |
| Examples: | open data4-1 |
| open voter.dta | |
| open fedbog.bin --www | |
| open dbnomics |
Opens a data file or database—see chapter 4 of the Gretl User's Guide for an explanation of this distinction. The effect is somewhat different in the two cases. When a data file is opened, its content is read into gretl's workspace, replacing the current dataset (if any). To add data to the current dataset instead of replacing, see append or (for greater flexibility) join. When a database is opened this does not immediately load any data; rather, it sets the source for subsequent invocations of the data command, which is used to import selected series. For specifics regarding databases see the section headed "Opening a database" below.
If filename is not given as a full path, gretl will search some relevant paths to try to find the file, with workdir as a first choice. If no filename suffix is given (as in the first example above), gretl assumes a native datafile with suffix .gdt. Based on the name of the file and various heuristics, gretl will try to detect the format of the data file (native, plain text, CSV, MS Excel, Stata, SPSS, etc.).
If the --frompkg option is used, gretl will look for the specified data file in the subdirectory associated with the function package specified by pkgname.
If the filename argument takes the form of a URI starting with http:// or https://, then gretl will attempt to download the indicated data file before opening it.
By default, opening a new data file clears the current gretl session, which includes deletion of all named variables, including matrices, scalars and strings. If you wish to keep your currently defined variables (other than series, which are necessarily cleared out), use the --preserve option.
When opening a data file in a spreadsheet format (Gnumeric, Open Document or MS Excel), you may give up to three additional parameters following the filename. First, you can select a particular worksheet within the file. This is done either by giving its (1-based) number, using the syntax, e.g., --sheet=2, or, if you know the name of the sheet, by giving the name in double quotes, as in --sheet="MacroData". The default is to read the first worksheet. You can also specify a column and/or row offset into the worksheet via, e.g.,
--coloffset=3 --rowoffset=2
which would cause gretl to ignore the first 3 columns and the first 2 rows. The default is an offset of 0 in both dimensions, that is, to start reading at the top-left cell.
With plain text files, gretl generally expects to find the data columns delimited in some standard manner (generally via comma, tab, space or semicolon). By default gretl looks for observation labels or dates in the first column if its heading is empty or is a suggestive string such as "year", "date" or "obs". You can prevent gretl from treating the first column specially by giving the --all-cols option.
A "fixed format" text data file is one without column delimiters, but in which the data are laid out according to a known set of specifications such as "variable k occupies 8 columns starting at column 24". To read such files, you should append a string --fixed-cols=colspec, where colspec is composed of comma-separated integers. These integers are interpreted as a set of pairs. The first element of each pair denotes a starting column, measured in bytes from the beginning of the line with 1 indicating the first byte; and the second element indicates how many bytes should be read for the given field. So, for example, if you say
open fixed.txt --fixed-cols=1,6,20,3
then for variable 1 gretl will read 6 bytes starting at column 1; and for variable 2, 3 bytes starting at column 20. Lines that are blank, or that begin with #, are ignored, but otherwise the column-reading template is applied, and if anything other than a valid numerical value is found an error is flagged. If the data are read successfully, the variables will be named v1, v2, etc. It's up to the user to provide meaningful names and/or descriptions using the commands rename and/or setinfo.
By default, when you import a file that contains string-valued series, a text box will open showing you the contents of string_table.txt, a file which contains the mapping between strings and their numeric coding. You can suppress this behavior via the --quiet option.
Use of open with a data file argument (as opposed to the database case, see below) generally implies loading all series from the specified file. However, in the case of native gretl files (gdt and gdtb) only, it is possible to specify by name a subset of series to load. This is done via the --select option, which requires an accompanying argument in one of three forms: the name of a single series; a list of names, separated by spaces and enclosed in double quotes; or the name of an array of strings. Examples:
# single series
open somefile.gdt --select=x1
# more than one series
open somefile.gdt --select="x1 x5 x27"
# alternative method
strings Sel = defarray("x1", "x5", "x27")
open somefile.gdt --select=Sel
As mentioned above, the open command can be used to open a database file for subsequent reading via the data command. Supported file-types are native gretl databases, RATS 4.0 and PcGive.
Besides reading a file of one of these types on the local machine, three further cases are supported. First, if the --www option is given, gretl will try to access a native gretl database of the given name on the gretl server—for instance the Federal Reserve interest rates database fedbog.bin in the third example shown above. Second, the command "open dbnomics" can be used to set DB.NOMICS as the source for database reads; on this see dbnomics for gretl. Third, if the --odbc option is given gretl will try to access an ODBC database. This option is explained at length in chapter 43 of the Gretl User's Guide.
Menu path: /File/Open data
Other access: Drag a data file onto gretl's main window| Argument: | varlist |
Applicable with panel data only. A series of forward orthogonal deviations is obtained for each variable in varlist and stored in a new variable with the prefix o_. Thus orthdev x y creates the new variables o_x and o_y.
The values are stored one step ahead of their true temporal location (that is, o_x at observation t holds the deviation that, strictly speaking, belongs at t – 1). This is for compatibility with first differences: one loses the first observation in each time series, not the last.
| Variants: | outfile filename |
| outfile --buffer=strvar | |
| outfile --tempfile=strvar | |
| Options: | --append (append to file, first variant only) |
| --quiet (see below) | |
| --buffer (see below) | |
| --tempfile (see below) | |
| --decpoint (see below) |
The outfile command starts a block in which any printed output is diverted to a file or buffer (or just discarded, if you wish). Such a block is terminated by the command "end outfile", after which output reverts to the default stream.
The first variant shown above sends output to a file named by the filename argument. By default a new file is created (or an existing one is overwritten). The output file will be written in the currently set workdir, unless the filename string contains a full path specification to the contrary. If you wish to append output to an existing file instead, use the --append flag.
A simple example follows, where the output from a particular regression is written to a named file.
open data4-10 outfile regress.txt ols ENROLL 0 CATHOL INCOME COLLEGE end outfile
Three special values for filename are supported, as follows:
null: printed output is suppressed until redirection is ended.
stdout: output is redirected to the "standard output" stream.
stderr: output is redirected to the "standard error" stream.
The --buffer option is used to store output in a string variable. The required parameter for this option must be the name of an existing string variable, whose content will be over-written. We show below the example given above, revised to write to a string. In this case printing model_out will display the redirected output.
open data4-10 string model_out = "" outfile --buffer=model_out ols ENROLL 0 CATHOL INCOME COLLEGE end outfile print model_out
The --tempfile option is used to direct output to a temporary file, with an automatically constructed name that is guaranteed to be unique, in the user's "dot" directory. As in the redirection to buffer case, the option parameter should be the name of a string variable: in this case its content is over-written with the name of the temporary file. Please note: files written to the dot directory are cleaned up on exit from the program, so don't use this form if you want the output to be preserved after your gretl session.
We repeat the simple example from above, with a couple of extra lines to illustrate the points that strvar tells you where the output went, and you can retrieve it using the readfile function.
open data4-10 string mytemp outfile --tempfile=mytemp ols ENROLL 0 CATHOL INCOME COLLEGE end outfile printf "Output went to %s\n", mytemp printf "The output was:\n%s\n", readfile(mytemp) # clean up if the file is no longer needed remove(mytemp)
In some cases you may wish to exercise some control over the name of the temporary file. You can do this by supplying a string variable which contains six consecutive Xs, as in
string mytemp = "tmpXXXXXX.csv" outfile --tempfile=mytemp ...
In this case XXXXXX will be replaced by random characters that ensure uniqueness of the filename, but the ".csv" suffix will be preserved. As in the simpler case above, the file is automatically written into the user's "dot" directory and the content of the string variable passed via the option flag is modified to hold the full path to the temporary file.
The effect of the --quiet option is to turn off the echoing of commands and the printing of auxiliary messages while output is redirected. It is equivalent to doing
set echo off set messages off
except that when redirection is ended the original values of the echo and messages variables are restored. This option is available in all cases.
The effect of the --decpoint option is ensure that the decimal point character (as opposed to comma) is in force while output is redirected. When the outfile block ends the decimal character reverts to whatever was in place before it. This option is especially useful if the text file to be created is meant as an input for some other program that requires digits to follow the English convention, as would be the case, for example, of a gnuplot or R script.
In general only one file can be opened in this way at any given time, so calls to this command cannot be nested. However, use of this command is permitted inside user-defined functions (provided the output file is also closed from inside the same function) such that output can be temporarily diverted and then given back to an original output file, in case outfile is currently in use by the caller. For example, the code
function void f (string s)
outfile inner.txt
print s
end outfile
end function
outfile outer.txt --quiet
print "Outside"
f("Inside")
print "Outside again"
end outfile
will produce a file called "outer.txt" containing the two lines
Outside Outside again
and a file called "inner.txt" containing the line
Inside
| Arguments: | depvar indepvars |
| Options: | --vcv (print covariance matrix) |
| --fixed-effects (estimate with group fixed effects) | |
| --random-effects (random effects or GLS model) | |
| --nerlove (use the Nerlove transformation) | |
| --pooled (estimate via pooled OLS) | |
| --between (estimate the between-groups model) | |
| --robust (robust standard errors; see below) | |
| --cluster=cvar (clustered standard errors; see below) | |
| --time-dummies (include time dummy variables) | |
| --unit-weights (weighted least squares) | |
| --iterate (iterative estimation) | |
| --matrix-diff (compute Hausman test via matrix difference) | |
| --unbalanced=method (random effects only, see below) | |
| --quiet (less verbose output) | |
| --verbose (more verbose output) | |
| Examples: | penngrow.inp, panel-robust.inp |
Estimates a panel model. By default the fixed effects estimator is used; this is implemented by subtracting the group or unit means from the original data.
If the --random-effects flag is given, random effects estimates are computed, by default using the method of Swamy and Arora (1972). In this case (only) the option --matrix-diff forces use of the matrix-difference method (as opposed to the regression method) for carrying out the Hausman test for the consistency of the random effects estimator. Also specific to the random effects estimator is the --nerlove flag, which selects the method of Nerlove (1971) as opposed to Swamy and Arora.
Alternatively, if the --unit-weights flag is given, the model is estimated via weighted least squares, with the weights based on the residual variance for the respective cross-sectional units in the sample. In this case (only) the --iterate flag may be added to produce iterative estimates: if the iteration converges, the resulting estimates are Maximum Likelihood.
As a further alternative, if the --between flag is given, the between-groups model is estimated (that is, an OLS regression using the group means).
The default means of calculating robust standard errors in panel-data models is the HAC estimator of Arellano (2003) (clustered by panel unit). Alternatives are "Panel Corrected Standard Errors" (Beck and Katz, 1995) and "Spatial Correlation Consistent" standard errors (Driscoll and Kraay, 1998). These can be selected via the command set panel_robust with arguments pcse and scc, respectively. Other alternatives to these three options are available via the --cluster option; please see chapter 22 of the Gretl User's Guide for details. When robust standard errors are specified the joint F test on the fixed effects is performed using the robust method of Welch (1951).
The --unbalanced option is available only for random effects models: it can be used to choose an ANOVA method for use with an unbalanced panel. By default gretl uses the Swamy–Arora method as for balanced panels, except that the harmonic mean of the individual time-series lengths is used in place of a common T. Under this option you can specify either bc, to use the method of Baltagi and Chang (1994), or stata, to emulate the sa option to the xtreg command in Stata.
For more details on panel estimation, please see chapter 23 of the Gretl User's Guide.
Menu path: /Model/Panel
| Argument: | plotvar |
| Options: | --means (time series, group means) |
| --overlay (plot per group, overlaid, N <= 130) | |
| --sequence (plot per group, in sequence, N <= 130) | |
| --grid (plot per group, in grid, N <= 16) | |
| --stack (plot per group, stacked, N <= 6) | |
| --boxplots (boxplot per group, in sequence, N <= 150) | |
| --boxplot (single boxplot, all groups) | |
| --output=filename (send output to specified file) | |
| Examples: | panplot x --overlay |
| panplot x --means --output=display |
Graphing command specific to panel data: the series plotvar is plotted in a mode specified by one or other of the options.
Apart from the --means and --boxplot options the plot explicitly represents variation in both the time-series and cross-sectional dimensions. Such plots are limited in respect of the number of groups (also known as individuals or units) in the current sample range of the panel. For example, the --overlay option, which shows a time series for each group in a single plot, is available only when the number of groups, N, is 130 or less. (Otherwise the graphic becomes too dense to be informative.) If a panel is too large to permit the desired plot specification one can select a reduced range of groups or units temporarily, as in
smpl 1 100 --unit panplot x --overlay smpl full
The --output=filename option can be used to control the form and destination of the output; see the gnuplot command for details.
Other access: Main window pop-up menu (single selection)| Options: | --nerlove (use Nerlove method for random effects) |
| --matrix_diff (use matrix-difference method for Hausman test) | |
| --quiet (Suppress printed output) |
This command is available only after estimating a panel-data model via OLS. It tests the simple pooled specification against the most common alternatives, fixed effects and random effects.
The fixed effects specification allows the intercept of the regression to vary across the cross-sectional units. A Wald F-test is reported for the null hypotheses that the intercepts do not differ. The random effects specification decomposes the residual variance into two parts, one part specific to the cross-sectional unit and the other specific to the particular observation. (This estimator can be computed only if the number of cross-sectional units in the data set exceeds the number of parameters to be estimated.) The Breusch–Pagan LM statistic tests the null hypothesis that pooled OLS is adequate against the random effects alternative.
Pooled OLS may be rejected against both of the alternatives. Provided the unit- or group-specific error is uncorrelated with the independent variables, the random effects estimator is more efficient than fixed effects; otherwise the random effects estimator is inconsistent and fixed effects are to be preferred. The null hypothesis for the Hausman test is that the group-specific error is not so correlated (and therefore the random effects estimator is preferable). A low p-value for this test counts against random effects and in favor of fixed effects.
The first two options for this command pertain to random effects estimation. By default the method of Swamy and Arora is used, and the Hausman test statistic is calculated using the regression method. The options enable the use of Nerlove's alternative variance estimator, and/or the matrix-difference approach to the Hausman statistic.
On successful completion the accessors $test and $pvalue retrieve 3-vectors holding test statistics and p-values for the three tests noted above: poolability (Wald), poolability (Breusch–Pagan), and Hausman. If you just want the results in this form you can give the --quiet option to skip printed output.
Note that after estimating the random effects specification via the panel command, the Hausman test is automatically carried out and the results can be retrieved via the $hausman accessor.
Menu path: Model window, /Tests/Panel specification
| Argument: | varlist |
| Options: | --covariance (use the covariance matrix) |
| --save[=n] (save major components) | |
| --save-all (save all components) | |
| --quiet (don't print results) |
Principal Components Analysis. Unless the --quiet option is given, prints the eigenvalues of the correlation matrix (or the covariance matrix if the --covariance option is given) for the variables in varlist, along with the proportion of the joint variance accounted for by each component. Also prints the corresponding eigenvectors or "component loadings".
If you give the --save-all option then all components are saved to the dataset as series, with names PC1, PC2 and so on. These artificial variables are formed as the sum of (component loading) times (standardized Xi), where Xi denotes the ith variable in varlist.
If you give the --save option without a parameter value, components with eigenvalues greater than the mean (which means greater than 1.0 if the analysis is based on the correlation matrix) are saved to the dataset as described above. If you provide a value for n with this option then the most important n components are saved.
See also the princomp function.
Menu path: /View/Principal components
| Arguments: | series [ bandwidth ] |
| Options: | --bartlett (use Bartlett lag window) |
| --log (use log scale) | |
| --radians (show frequency in radians) | |
| --degrees (show frequency in degrees) | |
| --plot=mode-or-filename (see below) | |
| --silent (suppress printed output) |
Computes and displays the spectrum of the specified series. By default the sample periodogram is given, but optionally a Bartlett lag window is used in estimating the spectrum (see, for example, Greene's Econometric Analysis for a discussion of this). The default width of the Bartlett window is twice the square root of the sample size but this can be set manually using the bandwidth parameter, up to a maximum of half the sample size.
If the --log option is given the spectrum is represented on a logarithmic scale.
The (mutually exclusive) options --radians and --degrees influence the appearance of the frequency axis when the periodogram is graphed. By default the frequency is scaled by the number of periods in the sample, but these options cause the axis to be labeled from 0 to π radians or from 0 to 180°, respectively.
By default, if gretl is not in batch mode a plot of the periodogram is shown. This can be adjusted via the --plot option. The acceptable parameters to this option are none (to suppress the plot); display (to display a plot even when in batch mode); or a file name. The effect of providing a file name is as described for the --output option of the gnuplot command.
Menu path: /Variable/Periodogram
Other access: Main window pop-up menu (single selection)| Arguments: | action pkgname |
| Options: | --local (install from local file) |
| --quiet (see below) | |
| --verbose (see below) | |
| --staging (see below) | |
| Examples: | pkg install armax |
| pkg install /path/to/myfile.gfn --local | |
| pkg query ghosts | |
| pkg run-sample ghosts | |
| pkg unload armax |
This command provides a means of installing, unloading, querying or deleting gretl function packages. The action argument must be one of install, query, run‑sample, unload, remove or index. An extension to support data file packages is described below.
install: In the most basic form, with no option flag and the pkgname argument given as the "plain" name of a gretl function package (as in the first example above), the effect is to download the specified package from the gretl server (unless pkgname starts with http://) and install it on the local machine. In this case it is not necessary to supply a filename extension. If the --local option is given, however, pkgname should be the path to an uninstalled package file on the local machine, with the correct extension (.gfn or .zip). In this case the effect is to copy the file into place (gfn), or unzip it into place (zip), "into place" meaning where the include command will find it.
query: The default effect is to print basic information about the specified package (author, version, etc.). If the package includes extra resources (data files and/or additional scripts) a listing of these files is included. If the --quiet option is appended nothing is printed; the package information is instead stored in the form of a gretl bundle, which can be accessed via $result. If no information can be found this bundle will be empty.
run-sample: Provides a command-line means of running the sample script included in the specified package.
unload: pkgname should be given in plain form, without path or suffix as in the last example above. The effect is to unload the package in question from gretl's memory, if it is currently loaded, and also to remove it from the GUI menu to which it is attached, if any.
remove: performs the actions noted for unload and in addition deletes the file(s) associated with the package from disk.
index: is a special case in which pkgname must be replaced by the keyword "addons": the effect is to update the index of the standard packages known as addons. Such updating is performed automatically from time to time but in some cases a manual update may be useful. In this case the --verbose flag produces a printout of where gretl has searched and what it has found. To be clear, here's the way to get full indexing output:
pkg index addons --verbose
Besides its usage with function packages, the pkg install command can also be used with data file packages of the tar.gz type, as listed at https://gretl.sourceforge.net/gretl_data.html. For example, to install the Verbeek data files one can do
pkg install verbeek.tar.gz
Note that install is the only action supported operation for such files.
The --staging option is a convenience item for developers and is available only in conjunction with the install action as applied to a function package. Its effect is that the package in question is downloaded from the staging area at sourceforge rather than the public area. Packages in staging are not yet approved for general use, so ignore this option unless you know what you're doing.
Menu path: /File/Function packages/On server
| Argument: | [ data ] |
| Options: | --output=filename (send output to specified file) |
| --outbuf=stringname (send output to specified string) | |
| Examples: | nile.inp |
The plot block provides an alternative to the gnuplot command which may be more convenient when you are producing an elaborate plot (with several options and/or gnuplot commands to be inserted into the plot file). In addition to the following explanation, please also refer to chapter 6 of the Gretl User's Guide for some further examples.
A plot block starts with the command-word plot. This is commonly followed by a data argument, which specifies data to be plotted: this should be the name of a list, a matrix, or a single series. If no input data are specified the block must contain at least one directive to plot a formula instead; such directives may be given via literal or printf lines (see below).
If a list or matrix is given, the last element (list) or column (matrix) is assumed to be the x-axis variable and the other(s) the y-axis variable(s), unless the --time-series option is given in which case all the specified data go on the y axis. The option of supplying a single series name is restricted to time-series data, in which case it is assumed that a time-series plot is wanted; otherwise an error is flagged.
The starting line may be prefixed with the "savename <-" apparatus to save a plot as an icon in the GUI program. The block ends with end plot.
Inside the block you have zero or more lines of these types, identified by an initial keyword:
option: specify a single option.
options: specify multiple options on a single line, separated by spaces.
literal: a command to be passed to gnuplot literally.
printf: a printf statement whose result will be passed to gnuplot literally.
Note that besides --output and --outbuf, which should be appended to the line that ends the block, all the options supported by the gnuplot command are also supported by plot, but should be given within the block using the syntax described above. In this context it is not necessary to supply the customary double-dash before the option specifier. For details on the effects of the various options see gnuplot.
The intended use of the plot block is best illustrated by example:
string title = "My title" string xname = "My x-variable" plot plotmat options with-lines fit=none literal set linetype 3 lc rgb "#0000ff" literal set nokey printf "set title '%s'", title printf "set xlabel '%s'", xname end plot --output=display
This example assumes that plotmat is the name of a matrix with at least 2 columns (or a list with at least two members). Note that it is considered good practice to place the --output option (only) on the last line of the block; other options should be placed within the block.
The following example shows a case of specifying a plot without a data source.
plot literal set title 'CRRA utility' literal set xlabel 'c' literal set ylabel 'u(c)' literal set xrange[1:3] literal set key top left literal crra(x,s) = (x**(1-s) - 1)/(1-s) printf "plot crra(x, 0) t 'sigma=0', \\" printf " log(x) t 'sigma=1', \\" printf " crra(x,3) t 'sigma=3" end plot --output=display
| Arguments: | depvar indepvars [ ; offset ] |
| Options: | --robust (robust standard errors) |
| --cluster=clustvar (see logit for explanation) | |
| --vcv (print covariance matrix) | |
| --verbose (print details of iterations) | |
| --quiet (don't print results) | |
| Examples: | poisson y 0 x1 x2 |
| poisson y 0 x1 x2 ; S | |
| See also camtriv.inp, greene19_3.inp |
Estimates a poisson regression. The dependent variable is taken to represent the occurrence of events of some sort, and must take on only non-negative integer values.
If a discrete random variable Y follows the Poisson distribution, then
for y = 0, 1, 2,.... The mean and variance of the distribution are both equal to v. In the Poisson regression model, the parameter v is represented as a function of one or more independent variables. The most common version (and the only one supported by gretl) has
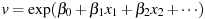
or in other words the log of v is a linear function of the independent variables.
Optionally, you may add an "offset" variable to the specification. This is a scale variable, the log of which is added to the linear regression function (implicitly, with a coefficient of 1.0). This makes sense if you expect the number of occurrences of the event in question to be proportional, other things equal, to some known factor. For example, the number of traffic accidents might be supposed to be proportional to traffic volume, other things equal, and in that case traffic volume could be specified as an "offset" in a Poisson model of the accident rate. The offset variable must be strictly positive.
By default, standard errors are computed using the negative inverse of the Hessian. If the --robust flag is given, then QML or Huber–White standard errors are calculated instead. In this case the estimated covariance matrix is a "sandwich" of the inverse of the estimated Hessian and the outer product of the gradient.
See also negbin.
Menu path: /Model/Limited dependent variable/Count data
| Variants: | print varlist |
| print object-names | |
| print string-literal | |
| Options: | --byobs (by observations) |
| --no-dates (use simple observation numbers) | |
| --range=start:stop (see below) | |
| --head[=lines] (see below) | |
| --tail[=lines] (see below) | |
| --midas (see below) | |
| --tree (specific to bundles; see below) | |
| Examples: | print x1 x2 --byobs |
| print my_matrix | |
| print "This is a string" | |
| print my_array --range=3:6 | |
| print hflist --midas |
Please note that print is a rather "basic" command (primarily intended for printing the values of series); see printf and eval for more advanced, and less restrictive, alternatives.
In the first variant shown above (also see the first example), varlist should be a list of series (either a named list or a list specified via the names or ID numbers of series, separated by spaces). In that case this command prints the values of the listed series. By default the data are printed "by variable", but if the --byobs flag (which can be abbreviated as -o) is added they are printed by observation. When printing by observation, the default is to show the date (with time-series data) or the observation marker string (if any) at the start of each line. The --no-dates option suppresses the printing of dates or markers; a simple observation number is shown instead. See the final paragraph of this entry for the effect of the --midas option (which applies only to a named list of series).
If no argument is given (the second variant shown above) then the action is similar to the first case except that all series in the current dataset are printed. The supported options are as decribed above.
The third variant (with the object-names argument; see the second example) expects a space-separated list of names of primary gretl objects other than series (scalars, matrices, strings, bundles, arrays). The value(s) of these objects are displayed. In the case of bundles, their members are sorted by type and alphabetically.
In the fourth form (third example), string-literal should be a string enclosed in double-quotes (and there should be nothing else following on the command line). The string in question is printed, followed by a newline character.
The --range option can be used to control the amount of information printed. The start and stop (integer) values refer to observations for series and lists, rows for matrices, elements for arrays, and lines of text for strings. In all cases the minimum start value is 1 and the maximum stop value is the "row-wise size" of the object in question. Negative values for these indices are taken to indicate a count back from the end. The indices may be given in numeric form or as the names of predefined scalar variables. If start is omitted that is taken as an implicit 1 and if stop is omitted that means go all the way to the end (an implicit -1). Note that with series and lists the indices are relative to the current sample range.
The --head and --tail options offer a quick way to show just the top or bottom of an object (rows for matrices, observations for series and lists, elements for arrays, lines for multi-line strings). The default number of lines printed in each case is 5; the optional parameter, which must be a positive integer, can be used to adjust this. Shorthand versions of these options are available: -h and -t, respectively, implying the default of 5 lines in each case. The following commands illustrate usage for a list L.
print L -h # show the first 5 lines print L --head=10 # the first 10 lines print L -t # show the last 5 lines print L --tail=3 # the last 3 lines
The --tree option is specific to the printing of a gretl bundle: the effect is that if the specified bundle contains further bundles, or arrays of bundles, their contents are listed. Otherwise only the top-level members of the bundle are listed.
The --midas option is specific to the printing of a list of series, and moreover it is specific to datasets that contain one or more high-frequency series, each represented by a MIDAS list. If one such list is given as argument and this option is appended, the series is printed by observation at its "native" frequency.
Menu path: /Data/Display values
| Arguments: | format , args |
Prints scalar values, series, matrices, or strings under the control of a format string (providing a subset of the printf function in the C programming language). Recognized numeric formats are %e, %E, %f, %g, %G, %d and %x, in each case with the various modifiers available in C. Examples: the format %.10g prints a value to 10 significant figures; %12.6f prints a value to 6 decimal places, with a width of 12 characters. Note, however, that in gretl the format %g is a good default choice for all numerical values; you don't need to get too complicated. The format %s should be used for strings.
The format string itself must be enclosed in double quotes. The values to be printed must follow the format string, separated by commas. These values should take the form of either (a) the names of variables, (b) expressions that yield some sort of printable result, or (c) the special functions varname() or date(). The following example prints the values of two variables plus that of a calculated expression:
ols 1 0 2 3
scalar b = $coeff[2]
scalar se_b = $stderr[2]
printf "b = %.8g, standard error %.8g, t = %.4f\n",
b, se_b, b/se_b
The next lines illustrate the use of the varname and date functions, which respectively print the name of a variable, given its ID number, and a date string, given a 1-based observation number.
printf "The name of variable %d is %s\n", i, varname(i) printf "The date of observation %d is %s\n", j, date(j)
If a matrix argument is given in association with a numeric format, the entire matrix is printed using the specified format for each element. The same applies to series, except that the range of values printed is governed by the current sample setting.
The maximum length of a format string is 127 characters. The escape sequences \n (newline), \r (carriage return), \t (tab), \v (vertical tab), \" (literal double-quote) and \\ (literal backslash) are recognized. To print a literal percent sign, use %%.
As in C, numerical values that form part of the format (width and or precision) may be given directly as numbers, as in %10.4f, or they may be given as variables. In the latter case, one puts asterisks into the format string and supplies corresponding arguments in order. For example,
scalar width = 12 scalar precision = 6 printf "x = %*.*f\n", width, precision, x
| Arguments: | depvar indepvars |
| Options: | --robust (robust standard errors) |
| --cluster=clustvar (see logit for explanation) | |
| --vcv (print covariance matrix) | |
| --verbose (print details of iterations) | |
| --quiet (don't print results) | |
| --p-values (show p-values instead of slopes) | |
| --estrella (select pseudo-R-squared variant) | |
| --random-effects (estimates a random effects panel probit model) | |
| --quadpoints=k (number of quadrature points for RE estimation) | |
| Examples: | ooballot.inp, oprobit.inp, reprobit.inp |
If the dependent variable is a binary variable (all values are 0 or 1) maximum likelihood estimates of the coefficients on indepvars are obtained via the Newton–Raphson method. As the model is nonlinear the slopes depend on the values of the independent variables. By default the slopes with respect to each of the independent variables are calculated (at the means of those variables) and these slopes replace the usual p-values in the regression output. This behavior can be suppressed by giving the --p-values option. The chi-square statistic tests the null hypothesis that all coefficients are zero apart from the constant.
By default, standard errors are computed using the negative inverse of the Hessian. If the --robust flag is given, then QML or Huber–White standard errors are calculated instead. In this case the estimated covariance matrix is a "sandwich" of the inverse of the estimated Hessian and the outer product of the gradient. See chapter 10 of Davidson and MacKinnon for details.
By default the pseudo-R-squared statistic suggested by McFadden (1974) is shown, but in the binary case if the --estrella option is given, the variant recommended by Estrella (1998) is shown instead. This variant arguably mimics more closely the properties of the regular R2 in the context of least-squares estimation.
If the dependent variable is not binary but is discrete, then Ordered Probit estimates are obtained. (If the variable selected as dependent is not discrete, an error is flagged.)
With the --random-effects option, the error term is assumed to be composed of two normally distributed components: one time-invariant term that is specific to the cross-sectional unit or "individual" (and is known as the individual effect); and one term that is specific to the particular observation.
Evaluation of the likelihood for this model involves the use of Gauss-Hermite quadrature for approximating the value of expectations of functions of normal variates. The number of quadrature points used can be chosen through the --quadpoints option (the default is 32). Using more points will increase the accuracy of the results, but at the cost of longer compute time; with many quadrature points and a large dataset estimation may be quite time consuming.
Besides the usual parameter estimates (and associated statistics) relating to the included regressors, certain additional information is presented on estimation of this sort of model:
lnsigma2: the maximum likelihood estimate of the log of the variance of the individual effect;
sigma_u: the estimated standard deviation of the individual effect; and
rho: the estimated share of the individual effect in the composite error variance (also known as the intra-class correlation).
The Likelihood Ratio test of the null hypothesis that rho equals zero provides a means of assessing whether the random effects specification is needed. If the null is not rejected that suggests that a simple pooled probit specification is adequate.
Menu path: /Model/Limited dependent variable/Probit
| Arguments: | dist [ params ] xval |
| Examples: | pvalue z zscore |
| pvalue t 25 3.0 | |
| pvalue X 3 5.6 | |
| pvalue F 4 58 fval | |
| pvalue G shape scale x | |
| pvalue B bprob 10 6 | |
| pvalue P lambda x | |
| pvalue W shape scale x | |
| See also mrw.inp, restrict.inp |
Computes the area to the right of xval in the specified distribution (z for Gaussian, t for Student's t, X for chi-square, F for F, G for gamma, B for binomial, P for Poisson, exp for Exponential, W for Weibull).
Depending on the distribution, the following information must be given, before the xval: for the t and chi-square distributions, the degrees of freedom; for F, the numerator and denominator degrees of freedom; for gamma, the shape and scale parameters; for the binomial distribution, the "success" probability and the number of trials; for the Poisson distribution, the parameter λ (which is both the mean and the variance); for the Exponential, a scale parameter; and for the Weibull, shape and scale parameters. As shown in the examples above, the numerical parameters may be given in numeric form or as the names of variables.
The parameters for the gamma distribution are sometimes given as mean and variance rather than shape and scale. The mean is the product of the shape and the scale; the variance is the product of the shape and the square of the scale. So the scale may be found as the variance divided by the mean, and the shape as the mean divided by the scale.
Menu path: /Tools/P-value finder
| Options: | --limit-to=list (limit test to subset of regressors) |
| --plot=mode-or-filename (see below) | |
| --quiet (suppress printed output) |
For a model estimated on time-series data via OLS, performs the Quandt likelihood ratio (QLR) test for a structural break at an unknown point in time, with 15 percent trimming at the beginning and end of the sample period.
For each potential break point within the central 70 percent of the observations, a Chow test is performed. See chow for details; as with the regular Chow test, this is a robust Wald test if the original model was estimated with the --robust option, an F-test otherwise. The QLR statistic is then the maximum of the individual test statistics.
An asymptotic p-value is obtained using the method of Bruce Hansen (1997).
Besides the standard hypothesis test accessors $test and $pvalue, $qlrbreak can be used to retrieve the index of the observation at which the test statistic is maximized.
The --limit-to option can be used to limit the set of interactions with the split dummy variable in the Chow tests to a subset of the original regressors. The parameter for this option must be a named list, all of whose members are among the original regressors. The list should not include the constant.
When this command is run interactively (only), a plot of the Chow test statistic is displayed by default. This can be adjusted via the --plot option. The acceptable parameters to this option are none (to suppress the plot); display (to display a plot even when not in interactive mode); or a file name. The effect of providing a file name is as described for the --output option of the gnuplot command.
Menu path: Model window, /Tests/QLR test
| Variants: | qqplot y |
| qqplot y x | |
| Options: | --z-scores (see below) |
| --raw (see below) | |
| --output=filename (send plot to specified file) |
Given just one series argument, displays a plot of the empirical quantiles of the selected series (given by name or ID number) against the quantiles of the normal distribution. The series must include at least 20 valid observations in the current sample range. By default the empirical quantiles are plotted against quantiles of the normal distribution having the same mean and variance as the sample data, but two alternatives are available: if the --z-scores option is given the data are standardized, while if the --raw option is given the "raw" empirical quantiles are plotted against the quantiles of the standard normal distribution.
The option --output has the effect of sending the output to the specified file; use "display" to force output to the screen. See the gnuplot command for more detail on this option.
Given two series arguments, y and x, displays a plot of the empirical quantiles of y against those of x. The data values are not standardized.
Menu path: /Variable/Normal Q-Q plot
Menu path: /View/Graph specified vars/Q-Q plot
| Arguments: | tau depvar indepvars |
| Options: | --robust (robust standard errors) |
| --intervals[=level] (compute confidence intervals) | |
| --vcv (print covariance matrix) | |
| --quiet (suppress printing of results) | |
| Examples: | quantreg 0.25 y 0 xlist |
| quantreg 0.5 y 0 xlist --intervals | |
| quantreg 0.5 y 0 xlist --intervals=.95 | |
| quantreg tauvec y 0 xlist --robust | |
| See also mrw_qr.inp |
Quantile regression. The first argument, tau, is the conditional quantile for which estimates are wanted. It may be given either as a numerical value or as the name of a pre-defined scalar variable; the value must be in the range 0.01 to 0.99. (Alternatively, a vector of values may be given for tau; see below for details.) The second and subsequent arguments compose a regression list on the same pattern as ols.
Without the --intervals option, standard errors are printed for the quantile estimates. By default, these are computed according to the asymptotic formula given by Koenker and Bassett (1978), but if the --robust option is given, standard errors that are robust with respect to heteroskedasticity are calculated using the method of Koenker and Zhao (1994).
When the --intervals option is chosen, confidence intervals are given for the parameter estimates instead of standard errors. These intervals are computed using the rank inversion method, and in general they are asymmetrical about the point estimates. The specifics of the calculation are inflected by the --robust option: without this, the intervals are computed on the assumption of IID errors (Koenker, 1994); with it, they use the robust estimator developed by Koenker and Machado (1999).
By default, 90 percent confidence intervals are produced. You can change this by appending a confidence level (expressed as a decimal fraction) to the intervals option, as in --intervals=0.95.
Instead of supplying a scalar, you may give as tau the name of a pre-defined matrix. In this case estimates are computed for all the given tau values and the results are printed in a special format, showing the sequence of quantile estimates for each regressor in turn.
When a vector of quantiles is specified, the accessors $coeff and $stderr provide k x n matrices, where k is the number of regressors and n the number of quantiles. You can also get a matrix holding the coefficients and standard errors in the format shown in the quantreg printout, under the key rq_sequence in the $model bundle.
Menu path: /Model/Robust estimation/Quantile regression
Exits from gretl's current modality.
When called from a script, execution of the script is terminated. If the context is gretlcli in batch mode, gretlcli itself exits, otherwise the program reverts to interactive mode.
When called from the GUI console, the console window is closed.
When called from gretlcli in interactive mode the program exits.
Note that this command cannot be called within functions or loops.
In no case does the quit command cause the gretl GUI program to exit. That is done via the Quit item under the File menu, or Ctrl+Q, or by clicking the close control on the title-bar of the main gretl window.
| Arguments: | series newname |
| Options: | --quiet (suppress printed output) |
| --case (change case of all series names, see below) | |
| Examples: | rename x2 income |
| rename --case=lower |
Without the --case option this command changes the name of series (identified by name or ID number) to newname. The new name must be of 31 characters maximum, must start with a letter, and must be composed of only letters, digits, and the underscore character. In addition, it must not be the name of an existing object of any kind.
The --case option allows changing the case of all series names in the currently open dataset. When using this option, no series or newname should be provided. The following case types are supported:
lower: Convert all series names to lowercase.
upper: Convert all series names to uppercase.
camel: Convert all series names to camel case, meaning that underscores are deleted and the following character (if any) is capitalized. For example, some_thing becomes someThing.
snake: Convert all series names to snake case, meaning that any capital letters (other than the first in the name) are converted to lowercase, with an underscore prepended. For example, someThing becomes some_thing.
Menu path: /Variable/Edit attributes
Other access: Main window pop-up menu (single selection)| Options: | --quiet (don't print the auxiliary regression) |
| --silent (don't print anything) | |
| --squares-only (compute the test using only the squares) | |
| --cubes-only (compute the test using only the cubes) | |
| --robust (use robust standard errors in auxiliary regression) |
Must follow the estimation of a model via OLS. Carries out Ramsey's RESET test for model specification (nonlinearity) by adding the squares and/or the cubes of the fitted values to the regression and calculating the F statistic for the null hypothesis that the coefficients on the added terms are zero. For numerical reasons, the squares and cubes are rescaled using the standard deviation of the fitted values.
Both the squares and the cubes are added unless one of the options --squares-only or --cubes-only is given.
The --silent option may be used if one plans to make use of the $test and/or $pvalue accessors to grab the results of the test.
The --robust option is implicit if the regression to be tested employed robust standard errors.
Menu path: Model window, /Tests/Ramsey's RESET
| Options: | --quiet (don't print restricted estimates) |
| --silent (don't print anything) | |
| --wald (system estimators only – see below) | |
| --bootstrap (bootstrap the test if possible) | |
| --full (OLS and VECMs only, see below) | |
| Examples: | hamilton.inp, restrict.inp |
Imposes a set of (usually linear) restrictions on either (a) the model last estimated or (b) a system of equations previously defined and named. In all cases the set of restrictions should be started with the keyword "restrict" and terminated with "end restrict".
In the single equation case the restrictions are always implicitly to be applied to the last model, and they are evaluated as soon as the restrict block is closed.
In the case of a system of equations (defined via the system command), the initial "restrict" may be followed by the name of a previously defined system of equations. If this is omitted and the last model was a system then the restrictions are applied to the last model. By default the restrictions are evaluated when the system is next estimated, using the estimate command. But if the --wald option is given the restriction is tested right away, via a Wald chi-square test on the covariance matrix. Note that this option will produce an error if a system has been defined but not yet estimated.
Depending on the context, the restrictions to be tested may be expressed in various ways. The simplest form is as follows: each restriction is given as an equation, with a linear combination of parameters on the left and a scalar value to the right of the equals sign (either a numerical constant or the name of a scalar variable).
In the single-equation case, parameters may be referenced in the form b[i], where i represents the position in the list of regressors (starting at 1), or b[varname], where varname is the name of the regressor in question. In the system case, parameters are referenced using b plus two numbers in square brackets. The leading number represents the position of the equation within the system and the second number indicates position in the list of regressors. For example b[2,1] denotes the first parameter in the second equation, and b[3,2] the second parameter in the third equation. The b terms in the equation representing a restriction may be prefixed with a numeric multiplier, for example 3.5*b[4].
Here is an example of a set of restrictions for a previously estimated model:
restrict b[1] = 0 b[2] - b[3] = 0 b[4] + 2*b[5] = 1 end restrict
And here is an example of a set of restrictions to be applied to a named system. (If the name of the system does not contain spaces, the surrounding quotes are not required.)
restrict "System 1" b[1,1] = 0 b[1,2] - b[2,2] = 0 b[3,4] + 2*b[3,5] = 1 end restrict
In the single-equation case the restrictions are by default evaluated via a Wald test, using the covariance matrix of the model in question. If the original model was estimated via OLS then the restricted coefficient estimates are printed; to suppress this, append the --quiet option flag to the initial restrict command. As an alternative to the Wald test, for models estimated via OLS or WLS only, you can give the --bootstrap option to perform a bootstrapped test of the restriction.
In the system case, the test statistic depends on the estimator chosen: a Likelihood Ratio test if the system is estimated using a Maximum Likelihood method, or an asymptotic F-test otherwise.
There are two alternatives to the method of expressing restrictions described above. First, a set of g restrictions on a k-vector of parameters, β, may be written compactly as Rβ – q = 0, where R is an g x k matrix and q is a g-vector. You can specify a restriction by giving the names of pre-defined, conformable matrices to be used as R and q, as in
restrict R = Rmat q = qvec end restrict
Second, in a variant that may be useful when restrict is used within a function, you can construct the set of restriction statements in the form of an array of strings. You then use the inject keyword with the name of the array. Here's a simple example:
strings RS = array(2) RS[1] = "b[1,2] = 0" RS[2] = "b[2,1] = 0" restrict inject RS end restrict
In actual usage of this method one would likely use sprintf to construct the strings, based on input to a function.
If you wish to test a nonlinear restriction (this is currently available for single-equation models only) you should give the restriction as the name of a function, preceded by "rfunc = ", as in
restrict rfunc = myfunction end restrict
The constraint function should take a single const matrix argument; this will be automatically filled out with the parameter vector. And it should return a vector which is zero under the null hypothesis, non-zero otherwise. The length of the vector is the number of restrictions. This function is used as a "callback" by gretl's numerical Jacobian routine, which calculates a Wald test statistic via the delta method.
Here is a simple example of a function suitable for testing one nonlinear restriction, namely that two pairs of parameter values have a common ratio.
function matrix restr (const matrix b) matrix v = b[1]/b[2] - b[4]/b[5] return v end function
On successful completion of the restrict command the accessors $test and $pvalue give the test statistic and its p-value.
When testing restrictions on a single-equation model estimated via OLS, or on a VECM, the --full option can be used to set the restricted estimates as the "last model" for the purposes of further testing or the use of accessors such as $coeff and $vcv. Note that some special considerations apply in the case of testing restrictions on Vector Error Correction Models. Please see chapter 33 of the Gretl User's Guide for details.
Menu path: Model window, /Tests/Linear restrictions
| Argument: | series |
| Options: | --trim (see below) |
| --quiet (suppress printed output) | |
| --output=filename (see below) |
Range–mean plot: this command creates a simple graph to help in deciding whether a time series, y(t), has constant variance or not. We take the full sample t=1,...,T and divide it into small subsamples of arbitrary size k. The first subsample is formed by y(1),...,y(k), the second is y(k+1), ..., y(2k), and so on. For each subsample we calculate the sample mean and range (= maximum minus minimum), and we construct a graph with the means on the horizontal axis and the ranges on the vertical. So each subsample is represented by a point in this plane. If the variance of the series is constant we would expect the subsample range to be independent of the subsample mean; if we see the points approximate an upward-sloping line this suggests the variance of the series is increasing in its mean; and if the points approximate a downward sloping line this suggests the variance is decreasing in the mean.
Besides the graph, gretl displays the means and ranges for each subsample, along with the slope coefficient for an OLS regression of the range on the mean and the p-value for the null hypothesis that this slope is zero. If the slope coefficient is significant at the 10 percent significance level then the fitted line from the regression of range on mean is shown on the graph. The t-statistic for the null, and the corresponding p-value, are recorded and may be retrieved using the accessors $test and $pvalue respectively.
If the --trim option is given, the minimum and maximum values in each sub-sample are discarded before calculating the mean and range. This makes it less likely that outliers will distort the analysis.
If the --quiet option is given, no graph is shown and no output is printed; only the t-statistic and p-value are recorded. Otherwise the form of the plot can be controlled via the --output option; this works as described in connection with the gnuplot command.
Menu path: /Variable/Range-mean graph
| Argument: | filename |
Executes the commands in filename then returns control to the interactive prompt. This command is intended for use with the command-line program gretlcli, or at the "gretl console" in the GUI program.
See also include.
Menu path: Run icon in script window
| Argument: | series |
| Options: | --difference (use first difference of variable) |
| --equal (positive and negative values are equiprobable) |
Carries out the nonparametric "runs" test for randomness of the specified series, where runs are defined as sequences of consecutive positive or negative values. If you want to test for randomness of deviations from the median, for a variable named x1 with a non-zero median, you can do the following:
series signx1 = x1 - median(x1) runs signx1
If the --difference option is given, the variable is differenced prior to the analysis, hence the runs are interpreted as sequences of consecutive increases or decreases in the value of the variable.
If the --equal option is given, the null hypothesis incorporates the assumption that positive and negative values are equiprobable, otherwise the test statistic is invariant with respect to the "fairness" of the process generating the sequence, and the test focuses on independence alone.
Menu path: /Tools/Nonparametric tests
| Arguments: | yvar ; xvars or yvars ; xvar |
| Options: | --with-lines (create line graphs) |
| --matrix=name (plot columns of named matrix) | |
| --output=filename (send output to specified file) | |
| Examples: | scatters 1 ; 2 3 4 5 |
| scatters 1 2 3 4 5 6 ; 7 | |
| scatters y1 y2 y3 ; x --with-lines |
Generates pairwise graphs of yvar against all the variables in xvars, or of all the variables in yvars against xvar. The first example above puts variable 1 on the y-axis and draws four graphs, the first having variable 2 on the x-axis, the second variable 3 on the x-axis, and so on. The second example plots each of variables 1 through 6 against variable 7 on the x-axis. Scanning a set of such plots can be a useful step in exploratory data analysis. The maximum number of plots is 16; any extra variable in the list will be ignored.
By default the data are shown as points, but if you give the --with-lines flag they will be line graphs.
For details on usage of the --output option, please see the gnuplot command.
If a named matrix is specified as the data source the x and y lists should be given as 1-based column numbers. Alternatively, if no lists are given, all the columns are plotted against time or an index variable.
See also tsplots for a simple means of producing multiple time-series plots, and gridplot for a more flexible way of combining plots in a grid.
Menu path: /View/Multiple graphs/X-Y scatters
| Argument: | varlist |
The seasonal difference of each variable in varlist is obtained and the result stored in a new variable with the prefix sd_. This command is available only for seasonal time series.
Menu path: /Add/Seasonal differences of selected variables
| Variants: | set variable value |
| set --to-file=filename | |
| set --from-file=filename | |
| set stopwatch | |
| set | |
| Examples: | set svd on |
| set csv_delim tab | |
| set horizon 10 | |
| set --to-file=mysettings.inp |
The most common use of this command is the first variant shown above, where it is used to set the value of a selected program parameter. This is discussed in detail below. The other uses are: with --to-file, to write a script file containing all the current parameter settings; with --from-file to read a script file containing parameter settings and apply them to the current session; with stopwatch to zero the gretl "stopwatch" which can be used to measure CPU time (see the entry for the $stopwatch accessor); or, if the word set is given alone, to print the current settings.
Values set via this comand remain in force for the duration of the gretl session unless they are changed by a further call to set. The parameters that can be set in this way are enumerated below. Note that the settings of hc_version, hac_lag and hac_kernel are used when the --robust option is given to an estimation command.
The available settings are grouped under the following categories: program interaction and behavior, numerical methods, random number generation, robust estimation, filtering, time series estimation, and interaction with GNU R.
These settings are used for controlling various aspects of the way gretl interacts with the user.
workdir: path. Sets the default directory for writing and reading files, whenever full paths are not specified.
use_cwd: on or off (the default). Governs the setting of workdir at start-up: if it's on, the working directory is inherited from the shell, otherwise it is set to whatever was selected in the previous gretl session.
echo: off or on (the default). Suppress or resume the echoing of commands in gretl's output.
messages: off or on (the default). Suppress or resume the printing of non-error messages associated with various commands, for example when a new variable is generated or when the sample range is changed.
verbose: off, on (the default) or comments. Acts as a "master switch" for echo and messages (see above), turning them both off or on simultaneously. The comments argument turns off echo and messages but preserves printing of comments in a script.
warnings: off or on (the default). Suppress or resume the printing of warning messages when numerical problems arise, for example a computation produces non-finite values or the convergence of an optimizer is questionable.
csv_delim: either comma (the default), space, tab or semicolon. Sets the column delimiter used when saving data to file in CSV format.
csv_write_na: the string used to represent missing values when writing data to file in CSV format. Maximum 7 characters; the default is NA.
csv_read_na: the string taken to represent missing values (NAs) when reading data in CSV format. Maximum 7 characters. The default depends on whether a data column is found to contain numerical data (mostly) or string values. For numerical data the following are taken as indicating NAs: an empty cell, or any of the strings NA, N.A., na, n.a., N/A, #N/A, NaN, .NaN, ., .., -999, and -9999. For string-valued data only a blank cell, or a cell containing an empty string, is counted as NA. These defaults can be reimposed by giving default as the value for csv_read_na. To specify that only empty cells are read as NAs, give a value of "". Note that empty cells are always read as NAs regardless of the setting of this variable.
csv_digits: a positive integer specifying the number of significant digits to use when writing data in CSV format. By default up to 15 digits are used depending on the precision of the original data. Note that CSV output employs the C library's fprintf function with "%g" conversion, which means that trailing zeros are dropped.
display_digits: an integer from 3 to 6, specifying the number of significant digits to use when displaying regression coefficients and standard errors (the default being 6). This setting can also be used to limit the number of digits shown by the summary command; in this case the default (and also the maximum) is 5.
mwrite_g: on or off (the default). When writing a matrix to file as text, gretl by default uses scientific notation with 18-digit precision, hence ensuring that the stored values are a faithful representation of the numbers in memory. When writing primary data with no more than 6 digits of precision it may be preferable to use %g format for a more compact and human-readable file; you can make this switch via set mwrite_g on.
force_decpoint: on or off (the default). Force gretl to use the decimal point character, in a locale where another character (most likely the comma) is the standard decimal separator.
loop_maxiter: one non-negative integer value (default 100000). Sets the maximum number of iterations that a while loop is allowed before halting (see loop). Note that this setting only affects the while variant; its purpose is to guard against inadvertently infinite loops. Setting this value to 0 has the effect of disabling the limit; use with caution.
max_verbose: off (the default), on or full. Controls the verbosity of commands and functions that use numerical optimization methods. The on choice applies only to functions (such as BFGSmax and NRmax) which work silently by default; the effect is to print basic iteration information. The full setting can be used to trigger more detailed output, including parameter values and their respective gradient for the objective function at each iteration. This choice applies both to functions of the above-mentioned sort and to commands that rely on numerical optimization such as arima, probit and mle. In the case of commands the effect is to make their --verbose option produce more detail. See also chapter 37 of the Gretl User's Guide.
debug: 1, 2 or 0 (the default). This is for use with user-defined functions. Setting debug to 1 is equivalent to turning messages on within all such functions; setting this variable to 2 has the additional effect of turning on max_verbose within all functions.
shell_ok: on or off (the default). Enable launching external programs from gretl via the system shell. This is disabled by default for security reasons, and can only be enabled via the graphical user interface (Tools/Preferences/General). However, once set to on, this setting will remain active for future sessions until explicitly disabled.
bfgs_verbskip: one integer. This setting affects the behavior of the --verbose option to those commands that use BFGS as an optimization algorithm and is used to compact output. if bfgs_verbskip is set to, say, 3, then the --verbose switch will only print iterations 3, 6, 9 and so on.
skip_missing: on (the default) or off. Controls gretl's behavior when contructing a matrix from data series: the default is to skip data rows that contain one or more missing values but if skip_missing is set off missing values are converted to NaNs.
matrix_mask: the name of a series, or the keyword null. Offers greater control than skip_missing when constructing matrices from series: the data rows selected for matrices are those with non-zero (and non-missing) values in the specified series. The selected mask remains in force until it is replaced, or removed via the null keyword.
quantile_type: must be one of Q6 (the default), Q7 or Q8. Selects the specific method used by the quantile function. For details see Hyndman and Fan (1996) or the Wikipedia entry at https://en.wikipedia.org/wiki/Quantile.
huge: a large positive number (by default, 1.0E100). This setting controls the value returned by the accessor $huge.
assert: off (the default), warn or stop. Controls the consequences of failure (return value of 0) from the assert function.
datacols: an integer from 1 to 15, with default value 5. Sets the maximum number of series shown side-by-side when data are displayed by observation.
plot_collection: on, auto or off. This setting affects the way plots are displayed during interactive use. If it's on, plots of the same pixel size are gathered in a "plot collection", that is a single output window in which you can browse through the various plots going back and forth. With the off setting, instead, a different window for each plot will be generated, as in older gretl versions. Finally, the auto setting has the effect of enabling the plot collection mode only for graphs that are generated within 1.25 seconds from one another (for example, as a result of executing plotting commands in a loop).
These settings are used for controlling the numerical algorithms that gretl uses for estimation.
optimizer: either auto (the default), BFGS or newton. Sets the optimization algorithm used for various ML estimators, in cases where both BFGS and Newton–Raphson are applicable. The default is to use Newton–Raphson where an analytical Hessian is available, otherwise BFGS.
bhhh_maxiter: one integer, the maximum number of iterations for gretl's internal BHHH routine, which is used in the arma command for conditional ML estimation. If convergence is not achieved after bhhh_maxiter, the program returns an error. The default is set at 500.
bhhh_toler: one floating point value, or the string default. This is used in gretl's internal BHHH routine to check if convergence has occurred. The algorithm stops iterating as soon as the increment in the log-likelihood between iterations is smaller than bhhh_toler. The default value is 1.0E–06; this value may be re-established by typing default in place of a numeric value.
bfgs_maxiter: one integer, the maximum number of iterations for gretl's BFGS routine, which is used for mle, gmm and several specific estimators. If convergence is not achieved in the specified number of iterations, the program returns an error. The default value depends on the context, but is typically of the order of 500.
bfgs_toler: one floating point value, or the string default. This is used in gretl's BFGS routine to check if convergence has occurred. The algorithm stops as soon as the relative improvement in the objective function between iterations is smaller than bfgs_toler. The default value is the machine precision to the power 3/4; this value may be re-established by typing default in place of a numeric value.
bfgs_maxgrad: one floating point value. This is used in gretl's BFGS routine to check if the norm of the gradient is reasonably close to zero when the bfgs_toler criterion is met. A warning is printed if the norm of the gradient exceeds 1; an error is flagged if the norm exceeds bfgs_maxgrad. At present the default is the permissive value of 5.0.
bfgs_richardson: on or off (the default). Use Richardson extrapolation when computing numerical derivatives in the context of BFGS maximization.
initvals: the name of a predefined matrix. Allows manual setting of the initial parameter vector for certain estimation commands that involve numerical optimization: arma, garch, logit and probit, tobit and intreg, biprobit, duration, poisson, negbin, and also when imposing certain sorts of restriction associated with VECMs. Unlike other settings, initvals is not persistent: it resets to the default initializer after its first use. For details in connection with ARMA estimation see chapter 31 of the Gretl User's Guide.
lbfgs: on or off (the default). Use the limited-memory version of BFGS (L-BFGS-B) instead of the ordinary algorithm. This may be advantageous when the function to be maximized is not globally concave.
lbfgs_mem: an integer value in the range 3 to 20 (with a default value of 8). This determines the number of corrections used in the limited memory matrix when L-BFGS-B is employed.
nls_toler: a floating-point value. Sets the tolerance used in judging whether or not convergence has occurred in nonlinear least squares estimation using the nls command. The default value is the machine precision to the power 3/4; this value may be re-established by typing default in place of a numeric value.
svd: on or off (the default). Use SVD rather than Cholesky or QR decomposition in least squares calculations. This option applies to the mols function as well as various internal calculations, but not to the regular ols command.
force_qr: on or off (the default). This applies to the ols command. By default this command computes OLS estimates using Cholesky decomposition (the fastest method), with a fallback to QR if the data seem too ill-conditioned. You can use force_qr to skip the Cholesky step; in "doubtful" cases this may ensure greater accuracy.
fcp: on or off (the default). Use the algorithm of Fiorentini, Calzolari and Panattoni rather than native gretl code when computing GARCH estimates.
gmm_maxiter: one integer, the maximum number of iterations for gretl's gmm command when in iterated mode (as opposed to one- or two-step). The default value is 250.
nadarwat_trim: one integer, the trim parameter used in the nadarwat function.
fdjac_quality: one integer (0, 1 or 2), the algorithm used by the fdjac function; the default is 0.
gmp_bits: one integer, which should be an integral power of 2 (default and minimum value 256, maximum 8192). Controls the number of bits used to represent a floating point number when GMP (the GNU Multiple Precision Arithmetic Library) is called, primarily via the mpols command. Larger values give greater precision at the cost of longer compute time. This setting can also be controlled by the environment variable GRETL_MP_BITS.
seed: an unsigned integer or the keyword auto. Sets the seed for the pseudo-random number generator. By default this is set from the system time; if you want to generate repeatable sequences of random numbers you must set the seed manually. To reset the seed to a time-based automatic value, use auto.
use_dcmt: on (the default) or off. This setting is only used in the context of parallel execution via mpi. If on, as per default, each MPI process will use an independent random number generator. For more details, see gretl-mpi.pdf.
bootrep: an integer. Sets the number of replications for the restrict command with the --bootstrap option.
garch_vcv: unset, hessian, im (information matrix) , op (outer product matrix), qml (QML estimator), bw (Bollerslev–Wooldridge). Specifies the variant that will be used for estimating the coefficient covariance matrix, for GARCH models. If unset is given (the default) then the Hessian is used unless the "robust" option is given for the garch command, in which case QML is used.
arma_vcv: hessian (the default) or op (outer product matrix). Specifies the variant to be used when computing the covariance matrix for ARIMA models.
force_hc: off (the default) or on. By default, with time-series data and when the --robust option is given with ols, the HAC estimator is used. If you set force_hc to "on", this forces calculation of the regular Heteroskedasticity Consistent Covariance Matrix (HCCM), which does not take autocorrelation into account. Note that VARs are treated as a special case: when the --robust option is given the default method is regular HCCM, but the --robust-hac flag can be used to force the use of a HAC estimator.
robust_z: off (the default) or on. This controls the distribution used when calculating p-values based on robust standard errors in the context of least-squares estimators. By default gretl uses the Student t distribution but if robust_z is turned on the normal distribution is used.
hac_lag: nw1 (the default),
nw2, nw3 or an integer. Sets the
maximum lag value or bandwidth, p, used when
calculating HAC (Heteroskedasticity and Autocorrelation
Consistent) standard errors using the Newey-West approach, for
time series data. nw1 and nw2 represent
two variant automatic calculations based on the sample size,
T: for nw1,
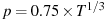 , and for nw2,
, and for nw2,
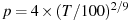 . nw3 calls for data-based
bandwidth selection. See also qs_bandwidth and
hac_prewhiten below.
. nw3 calls for data-based
bandwidth selection. See also qs_bandwidth and
hac_prewhiten below.
hac_kernel: bartlett (the default), parzen, or qs (Quadratic Spectral). Sets the kernel, or pattern of weights, used when calculating HAC standard errors.
hac_prewhiten: on or off (the default). Use Andrews-Monahan prewhitening and re-coloring when computing HAC standard errors. This also implies use of data-based bandwidth selection.
hac_missvals: es (the default), am or off. Sets the policy regarding calculation of HAC standard errors when the estimation sample includes incomplete observations: es invokes the Equal Spacing method of Datta and Du (2012); am selects the Amplitude Modulation method of Parzen (1963); and off causes gretl to refuse such estimation. See chapter 22 of the Gretl User's Guide for details.
hc_version: 0, 1, 2, 3 or 3a. Sets the variant used when calculating Heteroskedasticity Consistent standard errors with cross-sectional data. The first four options correspond to the HC0, HC1, HC2 and HC3 discussed by Davidson and MacKinnon in Econometric Theory and Methods, chapter 5. HC0 produces what are usually called "White's standard errors". Variant 3a is the MacKinnon–White "jackknife" procedure. The default setting is normally 1, but this can be changed in the GUI client, via the "HCCME" tab under "/Tools/Preferences/General". Note that a setting made via the GUI persists across gretl sessions, as opposed to use of the set command which just affects the current session.
panel_robust: arellano (the default), pcse or scc. This selects the robust covariance matrix estimator for use with panel-data models. See the panel command and chapter 22 of the Gretl User's Guide for details.
qs_bandwidth: Bandwidth for HAC estimation in the case where the Quadratic Spectral kernel is selected. (Unlike the Bartlett and Parzen kernels, the QS bandwidth need not be an integer.)
horizon: one integer (the default is based on the frequency of the data). Sets the horizon for impulse responses and forecast variance decompositions in the context of vector autoregressions.
vecm_norm: phillips (the default), diag, first or none. Used in the context of VECM estimation via the vecm command for identifying the cointegration vectors. See the chapter 33 of the Gretl User's Guide for details.
boot_iters: one integer, B. Sets the number of bootstrap iterations used when computing impulse response functions with confidence intervals. The default is 1999. It is recommended that B + 1 is evenly divisible by 100α/2, so for example with α = 0.1 B + 1 should be a multiple of 5. The minimum acceptable value is 499.
R_lib: on (the default) or off. When sending instructions to be executed by R, use the R shared library by preference to the R executable, if the library is available.
R_functions: off (the default) or on. Recognize functions defined in R as if they were native functions (the namespace prefix "R." is required). See chapter 45 of the Gretl User's Guide for details on this and the previous item.
mpi_use_smt: on or off (the default). This switch affects the default number of processes launched in an mpi block within a script. If the switch is off the default number of processes equals the number of physical cores on the local machine; if it's on the default is the maximum number of threads, which will be twice the number of physical cores if the cores support SMT (Simultaneous MultiThreading, also known as Hyper-Threading). This applies only if the user has not specified a number of processes, either directly or indirectly (by specifying a hosts file for use with MPI).
graph_theme: a string, one of altpoints, classic, dark2 (the current default), ethan, iwanthue or sober. This sets the "theme" used for graphs produced by gretl. The classic option reverts to the single theme that was in force prior to version 2020c of gretl.
| Argument: | series |
| Options: | --description=string (set description) |
| --graph-name=string (set graph name) | |
| --discrete (mark series as discrete) | |
| --continuous (mark series as continuous) | |
| --coded (mark as an encoding) | |
| --numeric (mark as not an encoding) | |
| --midas (mark as component of high-frequency data) | |
| Examples: | setinfo x1 --description="Description of x1" |
| setinfo y --graph-name="Some string" | |
| setinfo z --discrete |
If the options --description or --graph-name are invoked the argument must be a single series, otherwise it may be a list of series in which case it operates on all members of the list. This command sets up to four attributes as follows.
If the --description flag is given followed by a string in double quotes, that string is used to set the variable's descriptive label. This label is shown in response to the labels command, and is also shown in the main window of the GUI program.
If the --graph-name flag is given followed by a quoted string, that string will be used in place of the variable's name in graphs.
If one or other of the --discrete or --continuous option flags is given, the variable's numerical character is set accordingly. The default is to treat all series as continuous; setting a series as discrete affects the way the variable is handled in other commands and functions, such as for example freq or dummify .
If one or other of the --coded or --numeric option flags is given, the status of the given series is set accordingly. The default is to treat all numerical values as meaningful as such, at least in an ordinal sense; setting a series as coded means that the numerical values are an arbitrary encoding of qualitative characteristics.
The --midas option sets a flag indicating that a given series holds data of a higher frequency than the base frequency of the dataset; for example, the dataset is quarterly and the series holds values for month 1, 2 or 3 of each quarter. (MIDAS = Mixed Data Sampling.)
Menu path: /Variable/Edit attributes
Other access: Main window pop-up menu| Arguments: | value [ varlist ] |
| Examples: | setmiss -1 |
| setmiss 100 x2 |
Get the program to interpret some specific numerical data value (the first parameter to the command) as a code for "missing", in the case of imported data. If this value is the only parameter, as in the first example above, the interpretation will be applied to all series in the data set. If value is followed by a list of variables, by name or number, the interpretation is confined to the specified variable(s). Thus in the second example the data value 100 is interpreted as a code for "missing", but only for the variable x2.
Menu path: /Data/Set missing value code
| Variants: | setobs periodicity startobs |
| setobs unitvar timevar --panel-vars | |
| Options: | --cross-section (interpret as cross section) |
| --time-series (interpret as time series) | |
| --special-time-series (see below) | |
| --stacked-cross-section (interpret as panel data) | |
| --stacked-time-series (interpret as panel data) | |
| --panel-vars (use index variables, see below) | |
| --panel-time (see below) | |
| --panel-groups (see below) | |
| Examples: | setobs 4 1990:1 --time-series |
| setobs 12 1978:03 | |
| setobs 1 1 --cross-section | |
| setobs 20 1:1 --stacked-time-series | |
| setobs unit year --panel-vars |
This command forces the program to interpret the current data set as having a specified structure.
In the first form of the command the periodicity, which must be an integer, represents frequency in the case of time-series data (1 = annual; 4 = quarterly; 12 = monthly; 52 = weekly; 5, 6, or 7 = daily; 24 = hourly). In the case of panel data the periodicity means the number of lines per data block: this corresponds to the number of cross-sectional units in the case of stacked cross-sections, or the number of time periods in the case of stacked time series. In the case of simple cross-sectional data the periodicity should be set to 1.
The starting observation represents the starting date in the case of time series data. Years may be given with two or four digits; subperiods (for example, quarters or months) should be separated from the year with a colon. In the case of panel data the starting observation should be given as 1:1; and in the case of cross-sectional data, as 1. Starting observations for daily or weekly data should be given in the form YYYY-MM-DD (or simply as 1 for undated data).
Certain time-series periodicities have standard interpretations—for example, 12 = monthly and 4 = quarterly. If you have unusual time-series data to which the standard interpretation does not apply, you can signal this by giving the --special-time-series option. In that case gretl will not (for example) report your frequency-12 data as being monthly.
If no explicit option flag is given to indicate the structure of the data the program will attempt to guess the structure from the information given.
The second form of the command (which requires the --panel-vars flag) may be used to impose a panel interpretation when the data set contains variables that uniquely identify the cross-sectional units and the time periods. The data set will be sorted as stacked time series, by ascending values of the units variable, unitvar.
The --panel-time and --panel-groups options can only be used with a dataset which has already been defined as a panel.
The purpose of --panel-time is to set extra information regarding the time dimension of the panel. This should be given on the pattern of the first form of setobs noted above. For example, the following may be used to indicate that the time dimension of a panel is quarterly, starting in the first quarter of 1990.
setobs 4 1990:1 --panel-time
The purpose of --panel-groups is to create a string-valued series holding names for the groups (individuals, cross-sectional units) in the panel. (This will be used where appropriate in panel graphs.) With this option you supply either one or two arguments as follows.
First case: the (single) argument is the name of a string-valued series. If the number of distinct values equals the number of groups in the panel this series is used to define the group names. If necessary, the numerical content of the series will be adjusted such that the values are all 1s for the first group, all 2s for the second, and so on. If the number of string values doesn't match the number of groups an error is flagged.
Second case: the first argument is the name of a series and the second is a string literal or variable holding a name for each group. The series will be created if it does not already exist. If the second argument is a string literal or string variable the group names should be separated by spaces; if a name includes spaces it should be wrapped in backslash-escaped double-quotes. Alternatively the second argument may be an array of strings.
For example, the following will create a series named country in which the names in cstrs are each repeated T times, T being the time-series length of the panel.
string cstrs = sprintf("France Germany Italy \"United Kingdom\"")
setobs country cstrs --panel-groups
Menu path: /Data/Dataset structure
| Arguments: | command [ action ] options |
| Examples: | setopt mle --hessian |
| setopt ols persist --quiet | |
| setopt ols clear | |
| See also gdp_midas.inp |
This command enables the pre-setting of options for a specified command. Ordinarily this is not required, but it may be useful for the writers of hansl functions when they wish to make certain command options conditional on the value of an argument supplied by the caller.
For example, suppose a function offers a boolean "quiet" switch, whose intended effect is to suppress the printing of results from a certain regression executed within the function. In that case one might write:
if quiet setopt ols --quiet endif ols ...
The --quiet option will then be applied to the next ols command if and only if the variable quiet has a non-zero value.
By default, options set in this way apply only to the following instance of command; they are not persistent. However if you give persist as the value for action the options will continue to apply to the given command until further notice. The antidote to the persist action is clear: this erases any stored setting for the specified command.
It should be noted that options set via setopt are compounded with any options attached to the target command directly. So for example one might append the --hessian option to an mle command unconditionally but use setopt to add --quiet conditionally.
| Argument: | shellcommand |
| Examples: | ! ls -al |
| ! dir c:\users | |
| launch notepad | |
| launch emacs myfile.txt |
The facility described here is not activated by default. See below for details.
An exclamation mark, !, at the beginning of a command line is interpreted as an escape to the user's shell. Thus arbitrary shell commands can be executed from within gretl. The shellcommand argument is passed to /bin/sh on unix-type systems such as Linux and macOS or to cmd.exe on MS Windows. It is executed in synchronous mode—gretl waits for it to complete before proceeding. If the command outputs any text this is printed to the console or script output window.
A variant of synchronous shell access allows the user to "grab" the output of a command into a string variable. This is achieved by wrapping the command in parentheses, preceded by a dollar sign, as in
string s = $(ls -l $HOME)
The launch keyword, on the other hand, executes an external program asynchronously (without waiting for completion), as in the third and fourth examples above. This is designed for opening an application in interactive mode. The user's PATH is searched for the specified executable. On MS Windows the command is executed directly, not passed to cmd.exe (so environment variables are not expanded automatically).
For reasons of security the shell-access facility is not enabled by default. To activate it, check the box titled "Allow shell commands" under Tools/Preferences/General in the GUI program. This also makes shell commands available in the command-line program (and is the only way to do so).
| Variants: | smpl startobs endobs |
| smpl +i -j | |
| smpl dumvar --dummy | |
| smpl condition --restrict | |
| smpl --no-missing [ varlist ] | |
| smpl --no-all-missing [ varlist ] | |
| smpl --contiguous [ varlist ] | |
| smpl n --random | |
| smpl full | |
| smpl | |
| Options: | --dummy (argument is a dummy variable) |
| --restrict (apply boolean restriction) | |
| --replace (replace any existing boolean restriction) | |
| --no-missing (restrict to valid observations) | |
| --no-all-missing (omit empty observations (see below)) | |
| --contiguous (see below) | |
| --random (form random sub-sample) | |
| --permanent (see below) | |
| --preserve-panel (panel data: see below) | |
| --unit (panel data: sample in cross-sectional dimension) | |
| --time (panel data: sample in time-series dimension) | |
| --dates (interpret observation numbers as dates) | |
| --quiet (don't report sample range) | |
| Examples: | smpl 3 10 |
| smpl 1960:2 1982:4 | |
| smpl +1 -1 | |
| smpl x > 3000 --restrict | |
| smpl y > 3000 --restrict --replace | |
| smpl 100 --random |
This command can be used only when a dataset is in place. When no arguments are given, it displays the current sample range, otherwise it sets the sample range. The range can be defined in several ways. In the first alternate form (and the first two examples) above, startobs and endobs must be consistent with the periodicity of the data. Either one may be replaced by a semicolon to leave the value unchanged. (For more on startobs and endobs see the section titled "Dates versus sequential indices" below.) In the second form, the integers i and j (which may be positive or negative, and must be signed) are taken as offsets relative to the existing sample range. In the third form dummyvar must be an indicator variable with values 0 or 1 at each observation; the sample will be restricted to observations where the value is 1. The fourth form, using --restrict, restricts the sample to observations that satisfy the given Boolean condition.
The options --no-missing and --no-all-missing may be used to exclude from the sample observations for which data are missing. The first variant excludes those rows in the dataset for which at least one variable has a missing value, while the second excludes just those rows on which all variables have missing values. In each case the test is confined to the variables in varlist if this argument is given, otherwise it is applied to all series—with the qualification that in the case of --no-all-missing and no varlist, the generic variables index and time are ignored.
The --contiguous form of smpl is intended for use with time series data. The effect is to trim any observations at the start and end of the current sample range that contain missing values (either for the variables in varlist, or for all data series if no varlist is given). Then a check is performed to see if there are any missing values in the remaining range; if so, an error is flagged.
With the --random flag, the specified number of cases are selected from the current dataset at random (without replacement). If you wish to be able to replicate this selection you should set the seed for the random number generator first (see the set command).
The final form, smpl full, restores the full data range.
Note that sample restrictions are, by default, cumulative: the baseline for any smpl command is the current sample. If you wish the command to act so as to replace any existing restriction you can add the option flag --replace to the end of the command. (But this option is not compatible with the --contiguous option.)
The internal variable obs may be used with the --restrict form of smpl to exclude particular observations from the sample. For example
smpl obs!=4 --restrict
will drop just the fourth observation. If the data points are identified by labels,
smpl obs!="USA" --restrict
will drop the observation with label "USA".
One point should be noted about the --dummy, --restrict and --no-missing forms of smpl: "structural" information in the data file (regarding the time series or panel nature of the data) is likely to be lost when this command is issued. You may reimpose structure with the setobs command, but also see the --preserve-panel option below.
The --dates option can be used to resolve a potential ambiguity in the interpretation of startobs and endobs in the case of annual time-series data. For example, should 2010 be taken to refer to the year 2010, or to the two-thousand-and-tenth observation? In most cases this should come out right automatically but you can force the date interpretation if needed. This option can also be used with dated daily data, to get smpl to interpret, for example, 20100301 as the first of March 2010 rather than a plain sequential index. Note that this ambiguity does not arise with time series frequencies other than annual and daily; dates such as 1980:3 (third quarter of 1980) and 2020:03 (March 2020) cannot be confused with plain indices.
The --unit and --time options are specific to panel data. They allow you to specify, respectively, a range of "units" or time-periods. For example:
# limit the sample to the first 50 units smpl 1 50 --unit # limit the sample to periods 2 to 20 smpl 2 20 --time
If the time dimension of a panel dataset has been specified via the setobs command with the --panel-time option, smpl with the --time option can be expressed in terms of dates rather than plain observation numbers. Here's an example:
# specify panel time as quarterly, starting in Q1 of 1990 setobs 4 1990:1 --panel-time # limit the sample to 2000:1 to 2007:1 smpl 2000:1 2007:1 --time
In gretl, a panel dataset must always be "nominally balanced"—that is, each unit must have the same number of data rows, even if some rows contain nothing but NAs. Sub-sampling via the --restrict or --dummy options may destroy this structure. In that case the --preserve-panel flag can be added to request that a nominally balanced panel is reconstituted, via the insertion of "missing rows" if needed.
By default, restrictions on the current sample range can be undone: you can restore the full dataset via smpl full. However, the --permanent flag can be used to substitute the restricted dataset for the original. If you give the --permanent option with no other arguments or options the effect is to shrink the dataset to the current sample range.
Please see chapter 5 of the Gretl User's Guide for further details.
Menu path: /Sample
| Arguments: | series1 series2 |
| Option: | --verbose (print ranked data) |
Prints Spearman's rank correlation coefficient for the series series1 and series2. The variables do not have to be ranked manually in advance; the function takes care of this.
The automatic ranking is from largest to smallest (i.e. the largest data value gets rank 1). If you need to invert this ranking, create a new variable which is the negative of the original. For example:
series altx = -x spearman altx y
Menu path: /Tools/Nonparametric tests/Correlation
| Argument: | varlist |
| Option: | --cross (generate cross-products as well as squares) |
Generates new series which are squares of the series in varlist (plus cross-products if the --cross option is given). For example, square x y will generate sq_x = x squared, sq_y = y squared and (optionally) x_y = x times y. If a particular variable is a dummy variable it is not squared because we will get the same variable.
Menu path: /Add/Squares of selected variables
| Argument: | varlist |
| Options: | --no-df-corr (no degrees of freedom correction) |
| --center-only (don't divide by s.d.) |
By default a standardized version of each of the series in varlist is obtained and the result stored in a new series with the prefix s_. For example, stdize x y creates the new series s_x and s_y, each of which is centered and divided by its sample standard deviation (with a degrees of freedom correction of 1).
If the --no-df-corr option is given no degrees of freedom correction is applied; the standard deviation used is the maximum likelihood estimator. If --center-only is given the series just have their means subtracted, and in that case the output names have prefix c_ rather than s_.
The functionality of this command is available in somewhat more flexible form via the stdize function.
Menu path: /Add/Standardize selected variables
| Arguments: | filename [ varlist ] |
| Options: | --omit-obs (see below, on CSV format) |
| --no-header (see below, on CSV format) | |
| --gnu-octave (use GNU Octave format) | |
| --gnu-R (format friendly for read.table) | |
| --gzipped[=level] (apply gzip compression) | |
| --jmulti (use JMulti ASCII format) | |
| --dat (use PcGive ASCII format) | |
| --decimal-comma (use comma as decimal character) | |
| --database (use gretl database format) | |
| --overwrite (see below, on database format) | |
| --comment=string (see below) | |
| --matrix=matrix-name (see below) |
Save data to filename. By default all currently defined series are saved but the optional varlist argument can be used to select a subset of series. If the dataset is sub-sampled, only the observations in the current sample range are saved.
The output file will be written in the currently set workdir, unless the filename string contains a full path specification.
Note that the store command behaves in a special manner in the context of a "progressive loop"; see chapter 13 of the Gretl User's Guide for details.
If filename has extension .gdt or .gtdb this implies saving the data in one of gretl's native formats. In addition, if no extension is given .gdt is taken to be implicit and the suffix is added automatically. The gdt format is XML, optionally gzip-compressed, while the gdtb format is binary. The former is recommended for datasets of moderate size (say, up to several hundred kilobytes of data); the binary format is much faster for very large datasets.
When data are saved in gdt format the --gzipped option may be used for data compression. The optional parameter for this flag controls the level of compression (from 0 to 9): higher levels produce a smaller file, but compression takes longer. The default level is 1; a level of 0 means that no compression is applied.
A special sort of "native" save is supported in the GUI program: if filename has extension .gretl and the varlist argument is omitted, then a gretl session file is written. Such files include the current dataset along with any named objects such as models, graphs and matrices.
The format in which the data are written may be controlled to a degree by the extension or suffix of filename, as follows:
.csv: comma-separated values (CSV).
.txt or .asc: space-separated values.
.m: GNU Octave matrix format.
.dta: Stata dta format (version 113).
The format-related option flags shown above can be used to force the choice of format independently of the filename (or to get gretl to write in the formats of PcGive or JMulTi).
The option flags --omit-obs and --no-header are specific to saving data in CSV format. By default, if the data are time series or panel, or if the dataset includes specific observation markers, the output file includes a first column identifying the observations (e.g. by date). If the --omit-obs flag is given this column is omitted. The --no-header flag suppresses the usual printing of the names of the variables at the top of the columns.
The option flag --decimal-comma is also confined to CSV. Its effect is to replace the decimal point with decimal comma; in addition the column separator is forced to be a semicolon rather than a comma.
The option of saving in gretl database format is intended for construction of large sets of series with mixed frequencies and ranges of observations. At present this option is available only for annual, quarterly or monthly time-series data, or undated (cross-sectional) data. A gretl database takes the form of two files: one with suffix .bin to hold the data in binary form and a plain text file with suffix .idx for the metadata. In naming the output file on the command line you should either give the .bin suffix or no suffix.
When saving to a database that already exists, the default action is to append series to the prior content. In this context it is an error if any series to be saved has the same name as one already present. The --overwrite flag has the effect that, if there are variable names in common, the newly saved data replace the prior values.
The --comment option is available when saving data as a database or as CSV. The required parameter is a double-quoted one-line string, attached to the option flag with an equals sign. The string is inserted as a comment into the database index file or at the top of the CSV output.
The --matrix option requires a parameter, the name of a (non-empty) matrix. The effect of store is then, in effect, to turn the matrix into a dataset "in the background" and write it to file as such. Matrix columns become series; their names are taken from column-names attached to the matrix, if any, or by default are assigned as v1, v2 and so on. If the matrix has row names attached these are used as "observation markers" in the dataset.
Note that matrices can be written to file in their own right, see the mwrite function. But in some cases it may be useful to write them in dataset mode.
Menu path: /File/Save data; /File/Export data
| Variants: | summary [ varlist ] |
| summary --matrix=matname | |
| Options: | --simple (basic statistics only) |
| --weight=wtvar (weighting variable) | |
| --by=byvar (see below) | |
| Examples: | frontier.inp |
In its first form, this command prints summary statistics for the variables in varlist, or for all the variables in the data set if varlist is omitted. By default, output consists of the mean, median, minimum, maximum, standard deviation (sd), coefficient of variation (= sd/mean), skewness coefficient, excess kurtosis, 5th and 95th percentiles, inter-quartile range and number of missing observations. But if the --simple option is given, output is restricted to the mean, median, standard deviation, minimum and maximum.
If the --weight option is given, in which case the parameter wtvar should be the name of a series supplying weights per observation, the statistics are weighted accordingly.
If the --by option is given, in which case the parameter byvar should be the name of a discrete variable, then statistics are printed for sub-samples corresponding to the distinct values taken on by byvar. For example, if byvar is a (binary) dummy variable, statistics are given for the cases byvar=0 and byvar=1. Note: at present, this option is incompatible with the --weight option.
If the alternative form is given, using a named matrix, then summary statistics are printed for each column of the matrix. The --by option is not available in this case.
The table of statistics produced by summary can be retrieved in matrix form via the $result accessor. When the --by option is given, this accessor is produced only if varlist contains a single series.
See also the aggregate function for a more flexible means of producing "factorized" statistics.
Menu path: /View/Summary statistics
Other access: Main window pop-up menu| Variants: | system method=estimator |
| sysname <- system | |
| Examples: | "Klein Model 1" <- system |
| system method=sur | |
| system method=3sls | |
| See also klein.inp, kmenta.inp, greene14_2.inp |
Starts a system of equations. Either of two forms of the command may be given, depending on whether you wish to save the system for estimation in more than one way or just estimate the system once.
To save the system you should assign it a name, as in the first example (if the name contains spaces it must be surrounded by double quotes). In this case you estimate the system using the estimate command. With a saved system of equations, you are able to impose restrictions (including cross-equation restrictions) using the restrict command.
Alternatively you can specify an estimator for the system using method= followed by a string identifying one of the supported estimators: ols (Ordinary Least Squares), tsls (Two-Stage Least Squares) sur (Seemingly Unrelated Regressions), 3sls (Three-Stage Least Squares), fiml (Full Information Maximum Likelihood) or liml (Limited Information Maximum Likelihood). In this case the system is estimated once its definition is complete.
An equation system is terminated by the line end system. Within the system four sorts of statement may be given, as follows.
equation: specify an equation within the system.
instr: for a system to be estimated via Three-Stage Least Squares, a list of instruments (by variable name or number). Alternatively, you can put this information into the equation line using the same syntax as in the tsls command.
endog: for a system of simultaneous equations, a list of endogenous variables. This is primarily intended for use with FIML estimation, but with Three-Stage Least Squares this approach may be used instead of giving an instr list; then all the variables not identified as endogenous will be used as instruments.
identity: for use with FIML, an identity linking two or more of the variables in the system. This sort of statement is ignored when an estimator other than FIML is used.
After estimation using the system or estimate commands the following accessors can be used to retrieve additional information:
$uhat: the matrix of residuals, one column per equation.
$yhat: matrix of fitted values, one column per equation.
$coeff: column vector of coefficients (all the coefficients from the first equation, followed by those from the second equation, and so on).
$vcv: covariance matrix of the coefficients. If there are k elements in the $coeff vector, this matrix is k by k.
$sigma: cross-equation residual covariance matrix.
$sysGamma, $sysA and $sysB: structural-form coefficient matrices (see below).
If you want to retrieve the residuals or fitted values for a specific equation as a data series, select a column from the $uhat or $yhat matrix and assign it to a series, as in
series uh1 = $uhat[,1]
The structural-form matrices correspond to the following representation of a simultaneous equations model:
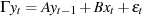
If there are n endogenous variables and k exogenous variables, Γ is an n x n matrix and B is n x k. If the system contains no lags of the endogenous variables then the A matrix is not present. If the maximum lag of an endogenous regressor is p, the A matrix is n x np.
Menu path: /Model/Simultaneous equations
| Options: | --output=filename (send output to specified file) |
| --format="f1|f2|f3|f4" (Specify custom TeX format) | |
| --complete (TeX-related, see below) |
Must follow the estimation of a model. Prints the model in tabular form. The format is governed by the extension of the specified filename: ".tex" for LaTeX, ".rtf" for RTF (Microsoft's Rich Text Format), or ".csv" for comma-separated. The file will be written in the currently set workdir, unless filename contains a full path specification.
If CSV format is selected, values are comma-separated unless the decimal comma is in force, in which case the separator is the semicolon.
If the --complete flag is given the LaTeX file is a complete document, ready for processing; otherwise it must be included in a document.
If you wish alter the appearance of the tabular output, you can specify a custom row format using the --format flag. The format string must be enclosed in double quotes and must be tied to the flag with an equals sign. The pattern for the format string is as follows. There are four fields, representing the coefficient, standard error, t-ratio and p-value respectively. These fields should be separated by vertical bars; they may contain a printf-type specification for the formatting of the numeric value in question, or may be left blank to suppress the printing of that column (subject to the constraint that you can't leave all the columns blank). Here are a few examples:
--format="%.4f|%.4f|%.4f|%.4f" --format="%.4f|%.4f|%.3f|" --format="%.5f|%.4f||%.4f" --format="%.8g|%.8g||%.4f"
The first of these specifications prints the values in all columns using 4 decimal places. The second suppresses the p-value and prints the t-ratio to 3 places. The third omits the t-ratio. The last one again omits the t, and prints both coefficient and standard error to 8 significant figures.
Once you set a custom format in this way, it is remembered and used for the duration of the gretl session. To revert to the default format you can use the special variant --format=default.
Menu path: Model window, /LaTeX
| Argument: | varlist |
| Options: | --time-series (plot by observation) |
| --one-scale (force a single scale) | |
| --tall (use 40 rows) |
Quick and simple ASCII graphics. Without the --time-series flag, varlist must contain at least two series, the last of which is taken as the variable for the x axis, and a scatter plot is produced. In this case the --tall option may be used to produce a graph in which the y axis is represented by 40 rows of characters (the default is 20 rows).
With the --time-series, a plot by observation is produced. In this case the option --one-scale may be used to force the use of a single scale; otherwise if varlist contains more than one series the data may be scaled. Each line represents an observation, with the data values plotted horizontally.
See also gnuplot.
| Arguments: | depvar indepvars |
| Options: | --llimit=lval (specify left bound) |
| --rlimit=rval (specify right bound) | |
| --vcv (print covariance matrix) | |
| --robust (robust standard errors) | |
| --opg (see below) | |
| --cluster=clustvar (see logit for explanation) | |
| --verbose (print details of iterations) | |
| --quiet (don't print results) |
Estimates a Tobit model, which may be appropriate when the dependent variable is "censored". For example, positive and zero values of purchases of durable goods on the part of individual households are observed, and no negative values, yet decisions on such purchases may be thought of as outcomes of an underlying, unobserved disposition to purchase that may be negative in some cases.
By default it is assumed that the dependent variable is censored at zero on the left and is uncensored on the right. However you can use the options --llimit and --rlimit to specify a different pattern of censoring. Note that if you specify a right bound only, the assumption is then that the dependent variable is uncensored on the left.
The Tobit model is a special case of interval regression. Please see the intreg command for further details, including an account of the --robust and --opg options.
Menu path: /Model/Limited dependent variable/Tobit
| Arguments: | depvar indepvars ; instruments |
| Options: | --no-tests (don't do diagnostic tests) |
| --vcv (print covariance matrix) | |
| --quiet (don't print results) | |
| --no-df-corr (no degrees-of-freedom correction) | |
| --robust (robust standard errors) | |
| --cluster=clustvar (clustered standard errors) | |
| --matrix-diff (compute Hausman test via matrix difference) | |
| --liml (use Limited Information Maximum Likelihood) | |
| --gmm (use the Generalized Method of Moments) | |
| Examples: | tsls y1 0 y2 y3 x1 x2 ; 0 x1 x2 x3 x4 x5 x6 |
| See also penngrow.inp |
Computes Instrumental Variables (IV) estimates, by default using two-stage least squares (TSLS) but see below for further options. The dependent variable is depvar, indepvars is the list of regressors (which is presumed to include at least one endogenous variable); and instruments is the list of instruments (exogenous and/or predetermined variables). If the instruments list is not at least as long as indepvars, the model is not identified.
In the above example, the ys are endogenous and the xs are the exogenous variables. Note that exogenous regressors should appear in both lists.
For details on the effects of the --robust and --cluster options, please see the help for ols.
Output for two-stage least squares estimates includes the Hausman test and, if the model is overidentified, the Sargan overidentification test. For a good explanation of both tests see chapter 8 of Davidson and MacKinnon (2004).
In the Hausman test, the null hypothesis is that OLS estimates are consistent, or in other words estimation by means of instrumental variables is not really required. By default this test is implemented by the regression method, but if the --matrix-diff option is given the method of Papadopoulos (2023) is used. In both cases a robust variant is employed if the --robust option is also given.
A model of this sort is overidentified if there are more instruments than are strictly required. The Sargan overidentification test (Sargan, 1958) is based on an auxiliary regression of the residuals from the two-stage least squares model on the full list of instruments. The null hypothesis is that all the instruments are valid, and suspicion is thrown on this hypothesis if the auxiliary regression has a significant degree of explanatory power.
These statistics are available, upon successful completion of the command, under the names $hausman and $sargan (if applicable), respectively.
For both TSLS and LIML estimation, an additional test result is shown provided that the model is estimated under the assumption of i.i.d. errors (that is, the --robust option is not selected). This is a test for weakness of the instruments. Weak instruments can lead to serious problems in IV regression: biased estimates and/or incorrect size of hypothesis tests based on the covariance matrix, with rejection rates well in excess of the nominal significance level (Stock, Wright and Yogo, 2002). The test statistic is the first-stage F-test if the model contains just one endogenous regressor, otherwise it is the smallest eigenvalue of the matrix counterpart of the first stage F. Critical values based on the Monte Carlo analysis of Stock and Yogo (2003) are shown when available.
The R-squared value printed for models estimated via two-stage least squares is the square of the correlation between the dependent variable and the fitted values.
As alternatives to TSLS, the model may be estimated via Limited Information Maximum Likelihood (the --liml option) or via the Generalized Method of Moments (--gmm option). Note that if the model is just identified these methods should produce the same results as TSLS, but if it is overidentified the results will differ in general.
If GMM estimation is selected, the following additional options become available:
--two-step: perform two-step GMM rather than the default of one-step.
--iterate: Iterate GMM to convergence.
--weights=Wmat: specify a square matrix of weights to be used when computing the GMM criterion function. The dimension of this matrix must equal the number of instruments. The default is an appropriately sized identity matrix.
Menu path: /Model/Instrumental variables
| Argument: | varlist |
| Options: | --matrix=name (plot columns of named matrix) |
| --output=filename (send output to specified file) | |
| Examples: | tsplots 1 2 3 4 |
| tsplots 1 2 3 4 --matrix=X |
Provides an easy way of plotting multiple time series (up to a maximum of 16) on a single canvas. The varlist argument can be given as a list of ID numbers or names of series, or as column numbers in the case of matrix input.
See also scatters for means of producing multiple scatterplots, and gridplot for a more flexible way of combining plots in a grid.
Menu path: /View/Multiple graphs/Time series
| Arguments: | order ylist [ ; xlist ] |
| Options: | --nc (do not include a constant) |
| --trend (include a linear trend) | |
| --seasonals (include seasonal dummy variables) | |
| --robust (robust standard errors) | |
| --robust-hac (HAC standard errors) | |
| --quiet (skip output of individual equations) | |
| --silent (don't print anything) | |
| --impulse-responses (print impulse responses) | |
| --variance-decomp (print variance decompositions) | |
| --lagselect (show criteria for lag selection) | |
| --minlag=minimum lag (lag selection only, see below) | |
| Examples: | var 4 x1 x2 x3 ; time mydum |
| var 4 x1 x2 x3 --seasonals | |
| var 12 x1 x2 x3 --lagselect | |
| See also sw_ch14.inp |
Sets up and estimates (using OLS) a vector autoregression (VAR). The first argument specifies the lag order — or the maximum lag order in case the --lagselect option is given (see below). The order may be given numerically, or as the name of a pre-existing scalar variable. Then follows the setup for the first equation. Do not include lags among the elements of ylist — they will be added automatically. The semi-colon separates the stochastic variables, for which order lags will be included, from any exogenous variables in xlist. Note that a constant is included automatically unless you give the --nc flag, a trend can be added with the --trend flag, and seasonal dummy variables may be added using the --seasonals flag.
While a VAR specification usually includes all lags from 1 to a given maximum, it is possible to select a specific set of lags. To do this, substitute for the regular (scalar) order argument either the name of a predefined vector or a comma-separated list of lags, enclosed in braces. We show below two ways of specifying that a VAR should include lags 1, 2 and 4 (but not lag 3):
var {1,2,4} ylist
matrix p = {1,2,4}
var p ylist
A separate regression is reported for each variable in ylist. Output for each equation includes F-tests for zero restrictions on all lags of each of the variables, an F-test for the significance of the maximum lag, and, if the --impulse-responses flag is given, forecast variance decompositions and impulse responses.
Forecast variance decompositions and impulse responses are based on the Cholesky decomposition of the contemporaneous covariance matrix, and in this context the order in which the (stochastic) variables are given matters. The first variable in the list is assumed to be "most exogenous" within-period. The horizon for variance decompositions and impulse responses can be set using the set command. For retrieval of a specified impulse response function in matrix form, see the irf function.
If the --robust option is given, standard errors are corrected for heteroskedasticity. Alternatively, the --robust-hac option can be given to produce standard errors that are robust with respect to both heteroskedasticity and autocorrelation (HAC). In general the latter correction should not be needed if the VAR includes sufficient lags.
If the --lagselect option is given, the usual VAR output is not presented. Instead the first argument is taken as the maximum lag order and the output consists of a table showing comparative figures computed for VARs of order 1 (by default) up to the specified maximum. The table includes log-likelihood and the P-value for a Likelihood Ratio (LR) test, followed by the Akaike (AIC), Schwarz (BIC) and Hannan–Quinn (HQC) information criteria. The LR test compares the specification on row i with that on row i – 1, the null hypothesis being that all the parameters added on row i have zero values. The table of results may be retrieved in matrix form via the $test accessor.
In the lag-selection context (only) the --minlag option can be used to adjust the minimum lag order. Set this to 0 to allow for the possibility that the optimal lag order is zero (meaning that a VAR is not really called for at all). Conversely you could set --minlag=4 if you believe you need at least 4 lags, thereby saving a little compute time.
Menu path: /Model/Multivariate time series
| Option: | --type=typename (scope of listing) |
By default, prints a listing of the series in the current dataset (if any); ls may be used as an alias.
If the --type option is given, it should be followed (after an equals sign) by one of the following typenames: series, scalar, matrix, list, string, bundle, array or accessor. The effect is to print the names of all currently defined objects of the named type.
As a special case, if the typename is accessor, the names printed are those of the internal variables currently available as "accessors", such as $nobs and $uhat, regardless of their specific type.
| Variants: | vartest x y |
| vartest x --split-by=dummy | |
| Options: | --quiet (suppress printed output) |
| --robust=method (see below) | |
| Examples: | vartest x y |
| meantest x --split-by=d | |
| meantest x y --robust=median | |
| meantest x y --robust=trimmed,5 |
In its primary usage, calculates the F statistic for the null hypothesis that the population variances are equal for the series x and y, and shows output including the p-value. Results can be retrieved using the accessors $test and $pvalue, in which case the --quiet option may used to omit the printout.
For example, the following code:
open AWM18.gdt
vartest EEN EXR
eval $test
eval $pvalue
produces the output shown below:
Equality of variances test
EEN: Number of observations = 192
EXR: Number of observations = 188
Ratio of sample variances = 3.70707
Null hypothesis: The two population variances are equal
Test statistic: F(191,187) = 3.70707
p-value (two-tailed) = 1.94866e-18
3.7070716
1.9486605e-18
In its alternate form, with the --split-by option, the samples whose variances are tested for equality are two subsets of the series x, for which the series dummy takes the values 0 and 1, respectively.
The standard F test rests on the assumption of normality and can over-reject substantially if the data are in fact non-normal. The --robust option offers three alternatives, as follows:
When method is mean, the test defined by Levene (1960). This is in effect a one-way ANOVA using the absolute deviations of the original data from their respective sample means.
When method is median, a variant on Levene's test suggested by Brown and Forsythe (1974), where the initial centering uses the sample median rather than the mean. This is recommended if the data are substantially skewed.
When method is trimmed, a second variant due to Brown and Forsythe, where centering is relative to a trimmed mean. This may be preferable if the data are fat-tailed but reasonably symmetrical. By default 10 percent trimming is employed (that is, the least and the greatest 10 percent of observations are omitted when calculating the mean) but this can be adjusted by appending a comma and an integer value, as in --robust=trimmed,5 which specifies 5 percent trimming.
Menu path: /Tools/Test statistic calculator
| Arguments: | order rank ylist [ ; xlist ] [ ; rxlist ] |
| Options: | --nc (no constant) |
| --rc (restricted constant) | |
| --uc (unrestricted constant) | |
| --crt (constant and restricted trend) | |
| --ct (constant and unrestricted trend) | |
| --seasonals (include centered seasonal dummies) | |
| --quiet (skip output of individual equations) | |
| --silent (don't print anything) | |
| --impulse-responses (print impulse responses) | |
| --variance-decomp (print variance decompositions) | |
| Examples: | vecm 4 1 Y1 Y2 Y3 |
| vecm 3 2 Y1 Y2 Y3 --rc | |
| vecm 3 2 Y1 Y2 Y3 ; X1 --rc | |
| See also denmark.inp, hamilton.inp |
A VECM is a form of vector autoregression or VAR (see var), applicable where the variables in the model are individually integrated of order 1 (that is, are random walks, with or without drift), but exhibit cointegration. This command is closely related to the Johansen test for cointegration (see johansen).
The order parameter to this command represents the lag order of the VAR system. The number of lags in the VECM itself (where the dependent variable is given as a first difference) is one less than order.
The rank parameter represents the cointegration rank, or in other words the number of cointegrating vectors. This must be greater than zero and less than or equal to (generally, less than) the number of endogenous variables given in ylist.
ylist supplies the list of endogenous variables, in levels. The inclusion of deterministic terms in the model is controlled by the option flags. The default if no option is specified is to include an "unrestricted constant", which allows for the presence of a non-zero intercept in the cointegrating relations as well as a trend in the levels of the endogenous variables. In the literature stemming from the work of Johansen (see for example his 1995 book) this is often referred to as "case 3". The first four options given above, which are mutually exclusive, produce cases 1, 2, 4 and 5 respectively. The meaning of these cases and the criteria for selecting a case are explained in chapter 33 of the Gretl User's Guide.
The optional lists xlist and rxlist allow you to specify sets of exogenous variables which enter the model either unrestrictedly (xlist) or restricted to the cointegration space (rxlist). These lists are separated from ylist and from each other by semicolons.
The --seasonals option, which may be combined with any of the other options, specifies the inclusion of a set of centered seasonal dummy variables. This option is available only for quarterly or monthly data.
The first example above specifies a VECM with lag order 4 and a single cointegrating vector. The endogenous variables are Y1, Y2 and Y3. The second example uses the same variables but specifies a lag order of 3 and two cointegrating vectors; it also specifies a "restricted constant", which is appropriate if the cointegrating vectors may have a non-zero intercept but the Y variables have no trend.
Following estimation of a VECM some special accessors are available: $jalpha, $jbeta and $jvbeta retrieve, respectively, the α and β matrices and the estimated variance of β. For retrieval of a specified impulse response function in matrix form, see the irf function.
Menu path: /Model/Multivariate time series
| Option: | --quiet (don't print anything) |
| Examples: | longley.inp |
Must follow the estimation of a model which includes at least two independent variables. Calculates and displays diagnostic information pertaining to collinearity.
The Variance Inflation Factor or VIF for regressor j is defined as
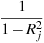
where Rj is the coefficient of multiple correlation between regressor j and the other regressors. The factor has a minimum value of 1.0 when the variable in question is orthogonal to the other independent variables. Neter, Wasserman, and Kutner (1990) suggest inspecting the largest VIF as a diagnostic for collinearity; a value greater than 10 is sometimes taken as indicating a problematic degree of collinearity.
Following this command the $result accessor may be used to retrieve a column vector holding the VIFs. For a more sophisticated approach to diagnosing collinearity, see the bkw command.
Menu path: Model window, /Analysis/Collinearity
| Arguments: | wtvar depvar indepvars |
| Options: | --vcv (print covariance matrix) |
| --robust (robust standard errors) | |
| --quiet (suppress printing of results) | |
| --allow-zeros (see below) |
Computes weighted least squares (WLS) estimates using wtvar as the weight, depvar as the dependent variable, and indepvars as the list of independent variables. Let w denote the positive square root of wtvar; then WLS is basically equivalent to an OLS regression of w * depvar on w * indepvars. The R-squared, however, is calculated in a special manner, namely as
where ESS is the error sum of squares (sum of squared residuals) from the weighted regression and WTSS denotes the "weighted total sum of squares", which equals the sum of squared residuals from a regression of the weighted dependent variable on the weighted constant alone.
As a special case, if wtvar is a 0/1 dummy variable, WLS estimation is equivalent to OLS on a sample that excludes all observations with value zero for wtvar. Otherwise including weights of zero is considered an error, but if you really want to mix zero weights with positive ones you can append the --allow-zeros option.
For weighted least squares estimation applied to panel data and based on the unit specific error variances please see the panel command with the --unit-weights option.
Menu path: /Model/Other linear models/Weighted Least Squares
| Arguments: | series1 series2 [ order ] |
| Options: | --plot=mode-or-filename (see below) |
| --quiet (suppress printed output) | |
| Example: | xcorrgm x y 12 |
Prints and/or graphs the cross-correlogram for series1 and series2, which may be specified by name or number. The values are the sample correlation coefficients between the current value of series1 and successive leads and lags of series2.
If an order value is specified the length of the cross-correlogram is limited to at most that number of leads and lags, otherwise the length is determined automatically, as a function of the frequency of the data and the number of observations.
By default, when gretl is not in batch mode a plot of the cross-correlogram is shown. This can be adjusted via the --plot option. The acceptable parameters to this option are none (to suppress the plot); display (to produce a gnuplot graph even when in batch mode); or a file name. The effect of providing a file name is as described for the --output option of the gnuplot command.
On successful completion of this command, $result retrieves the results in the form of a two-column matrix with lags in the first column and cross-correlations in the second.
Menu path: /View/Cross-correlogram
Other access: Main window pop-up menu (multiple selection)| Arguments: | ylist [ ; xlist ] |
| Options: | --row (display row percentages) |
| --column (display column percentages) | |
| --zeros (display zero entries) | |
| --no-totals (suppress printing of marginal counts) | |
| --matrix=matname (use frequencies from named matrix) | |
| --quiet (suppress printed output) | |
| --tex[=filename] (output as LaTeX) | |
| --equal (see the LaTeX case below) | |
| Examples: | xtab 1 2 |
| xtab 1 ; 2 3 4 | |
| xtab --matrix=A | |
| xtab 1 2 --tex="xtab.tex" | |
| See also ooballot.inp |
Given just the ylist argument, computes (and by default prints) a contingency table or cross-tabulation for each combination of the variables included in the list. If a second list xlist is given, each variable in ylist is cross-tabulated by row against each variable in xlist (by column). Variables in these lists can be referenced by name or by number. Note that all the variables must have been marked as discrete. Alternatively, if the --matrix option is given, the named matrix is treated as a precomputed set of frequencies, to be displayed as a cross-tabulation (see also the mxtab function). In this case the list argument(s) should be omitted.
By default the cell entries are given as frequency counts. The --row and --column options (which are mutually exclusive) replace the counts with the percentages for each row or column, respectively. By default, cells with a zero count are left blank but the --zeros option has the effect of showing zero counts explicitly, which may be useful for importing the table into another program, such as a spreadsheet.
Pearson's chi-square test for independence is shown if the expected frequency under independence is at least 1.0e-7 for all cells. A common rule of thumb for the validity of this statistic is that at least 80 percent of cells should have expected frequencies of 5 or greater; if this criterion is not met a warning is printed.
If the contingency table is 2 by 2, Fisher's Exact Test for independence is shown. Note that this test is based on the assumption that the row and column totals are fixed, which may or may not be appropriate depending on how the data were generated. The left p-value should be used when the alternative to independence is negative association (values tend to cluster in the lower left and upper right cells), the right p-value when the alternative is positive association. The two-tailed p-value for this test is calculated by method (b) in section 2.1 of Agresti (1992): it is the sum of the probabilities of all possible tables with the given row and column totals and a probability no greater than that of the observed table.
In the case of a bivariate cross-tabulation (only one list is given, and it has two members) certain results are stored. The contingency table may be retrieved in matrix form via the $result accessor. In addition, if the minimum expected value condition is met, the Pearson chi-square test and its p-value may be retrieved via the $test and $pvalue accessors. If it's these results that are of interest, the --quiet option can be used to suppress the usual printout.
If the --tex option is given the cross-tabulation is printed in the form of a LaTeX tabular environment, either inline (from where it may be copied and pasted) or, if the filename parameter is appended, to the specified file. (If filename does not specify a full path the file is written in the currently set workdir.) No test statistic is computed. The additional option --equal can be used to flag, by printing in boldface, the count or percentage for cells in which the row and column variables have the same numerical value. This option is ignored unless the --tex option is given, and also when one or both of the cross-tabulated variables are string-valued.