See also the Gretl Command Reference
The following accessors and functions are documented below.| $dotdir | $gnuplot | $gretldir | $lang | $seats | $tramo | $tramodir | $workdir |
| $x12a | $x12adir |
Must follow the estimation of a fixed-effects or random-effects panel data model. Returns a series containing the estimates of the individual effects.
Returns the Akaike Information Criterion for the last estimated model, if available. See chapter 28 of the Gretl User's Guide for details of the calculation.
Must follow estimation via ordered probit or logit, or multinomial logit. Returns an n x j matrix, where n is the number of observations used and j is the number of possible outcomes, holding the estimated probability of each outcome at each observation.
Returns Schwarz's Bayesian Information Criterion for the last estimated model, if available. See chapter 28 of the Gretl User's Guide for details of the calculation.
Returns the overall chi-square statistic from the last estimated model, if available.
| Argument: | s (name of coefficient, optional) |
With no arguments, $coeff returns a column vector containing the estimated coefficients for the last model. With the optional string argument it returns a scalar, namely the estimated parameter named s. See also $stderr, $vcv.
Example:
open bjg arima 0 1 1 ; 0 1 1 ; lg b = $coeff # gets a vector macoef = $coeff(theta_1) # gets a scalar
If the "model" in question is actually a system, the result depends on the characteristics of the system: for VARs and VECMs the value returned is a matrix with one column per equation, otherwise it is a column vector containing the coefficients from the first equation followed by those from the second equation, and so on.
Must follow the estimation of a model; returns the command word, for example ols or probit.
Must follow the estimation of a VAR or a VECM; returns the companion matrix.
Returns an integer value representing the sort of dataset that is currently loaded: 0 = no data; 1 = cross-sectional (undated) data; 2 = time-series data; 3 = panel data.
Must follow the estimation of a single-equation model; returns the name of the dependent variable.
Returns the degrees of freedom of the last estimated model. If the last model was in fact a system of equations, the value returned is the degrees of freedom per equation; if this differs across the equations then the value given is the number of observations minus the mean number of coefficients per equation (rounded up to the nearest integer).
Must follow estimation of a system of equations. Returns the P-value associated with the $diagtest statistic.
Must follow estimation of a system of equations. Returns the test statistic for the null hypothesis that the cross-equation covariance matrix is diagonal. This is the Breusch–Pagan test except when the estimator is (unrestricted) iterated SUR, in which case it is a Likelihood Ratio test. See chapter 34 of the Gretl User's Guide for details; see also $diagpval.
This accessor returns the path where gretl stores temporary files, for example when using the mwrite function with a non-zero third argument.
Returns the Durbin–Watson statistic for first-order serial correlation from the model last estimated (if available).
Returns the CDF of the Durbin–Watson distribution evaluated at the DW statistic for the model last estimated (if available), computed using the Imhof procedure. This is the p-value for a one-sided test with an alternative of positive first-order autocorrelation. If you want the p-value for a two-sided test, take 2P if DW < 2 or 2(1 – P) if DW > 2, where P is the value returned by the accessor.
Due to the limited precision of digital arithmetic, the Imhof integral can go negative when the Durbin–Watson statistic is close to its lower bound. In that case the accessor returns NA. Since any other failure mode results in an error being flagged it is probably safe to assume that an NA value means the true p-value is "very small", although we are unable to quantify it.
Must follow the estimation of a VECM; returns a matrix containing the error correction terms. The number of rows equals the number of observations used and the number of columns equals the cointegration rank of the system.
Returns the program's internal error code, which will be non-zero in case an error has occurred but has been trapped using catch. Note that using this accessor causes the internal error code to be reset to zero. If you want to get the error message associated with a given $error you need to store the value in a temporary variable, as in
err = $error if (err) printf "Got error %d (%s)\n", err, errmsg(err) endif
Returns the error sum of squares of the last estimated model, if available.
Must follow the estimation of a VECM; returns a vector containing the eigenvalues that are used in computing the trace test for cointegration.
Must follow the fcast forecasting command; returns the forecast values as a matrix. If the model on which the forecast was based is a system of equations the returned matrix will have one column per equation, otherwise it is a column vector.
Must follow the fcast forecasting command; returns the standard errors of the forecasts, if available, as a matrix. If the model on which the forecast was based is a system of equations the returned matrix will have one column per equation, otherwise it is a column vector.
Must follow estimation of a VAR. Returns a matrix containing the forecast error variance decomposition (FEVD). This matrix has h rows where h is the forecast horizon, which can be chosen using set horizon or otherwise is set automatically based on the frequency of the data.
For a VAR with p variables, the matrix has p2 columns: the first p columns contain the FEVD for the first variable in the VAR; the second p columns the FEVD for the second variable; and so on. The (decimal) fraction of the forecast error for variable i attributable to innovation in variable j is therefore found in column (i – 1)p + j.
For a more flexible variant of this functionality, see the fevd function.
Returns the overall F-statistic from the last estimated model, if available.
Must follow a gmm block. Returns the value of the GMM objective function at its minimum.
Must follow a garch command. Returns the estimated conditional variance series.
Must follow estimation of a model via either tsls or panel with the random effects option. Returns a 1 x 3 vector containing the value of the Hausman test statistic, the corresponding degrees of freedom and the p-value for the test, in that order.
Returns the Hannan-Quinn Information Criterion for the last estimated model, if available. See chapter 28 of the Gretl User's Guide for details of the calculation.
Returns a very large positive number. By default this is 1.0E100, but the value can be changed using the set command.
Must follow the estimation of a VECM, and returns the loadings matrix. It has as many rows as variables in the VECM and as many columns as the cointegration rank.
Must follow the estimation of a VECM, and returns the cointegration matrix. It has as many rows as variables in the VECM (plus the number of exogenous variables that are restricted to the cointegration space, if any), and as many columns as the cointegration rank.
Must follow the estimation of a VECM, and returns the estimated covariance matrix for the elements of the cointegration vectors.
In the case of unrestricted estimation, this matrix has a number of rows equal to the unrestricted elements of the cointegration space after the Phillips normalization. If, however, a restricted system is estimated via the restrict command with the --full option, a singular matrix with (n+m)r rows will be returned (n being the number of endogenous variables, m the number of exogenous variables that are restricted to the cointegration space, and r the cointegration rank).
Example: the code
open denmark.gdt vecm 2 1 LRM LRY IBO IDE --rc --seasonals -q s0 = $jvbeta restrict --full b[1,1] = 1 b[1,2] = -1 b[1,3] + b[1,4] = 0 end restrict s1 = $jvbeta print s0 print s1
produces the following output.
s0 (4 x 4)
0.019751 0.029816 -0.00044837 -0.12227
0.029816 0.31005 -0.45823 -0.18526
-0.00044837 -0.45823 1.2169 -0.035437
-0.12227 -0.18526 -0.035437 0.76062
s1 (5 x 5)
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.27398 -0.27398 -0.019059
0.0000 0.0000 -0.27398 0.27398 0.019059
0.0000 0.0000 -0.019059 0.019059 0.0014180
For selected models estimated via Maximum Likelihood, returns the series of per-observation log-likelihood values. At present this is supported only for binary logit and probit, tobit and heckit.
Returns the log-likelihood for the last estimated model (where applicable).
Returns the value of "machine epsilon", which gives an upper bound on the relative error due to rounding in double-precision floating point arithmetic.
If data from a GeoJSON file or ESRI shapefile have been loaded, returns the name of the file that should be opened to obtain the map polygons, otherwise returns an empty string. This is designed for use with the geoplot function.
Following estimation of a multinomial logit model (only), retrieves a matrix holding the estimated probabilities of each possible outcome at each observation in the model's sample range. Each row represents an observation and each column an outcome. As of gretl 2023a this accessor is deprecated: please use $allprobs instead.
Must follow estimation of a single-equation model; returns a bundle containing many items of data pertaining to the model. All the regular model accessors are included: these are referenced by keys that are the same as the regular accessor names, minus the leading dollar sign. So for example the residuals appear under the key uhat and the error sum of squares under ess.
Depending on the estimator, additional information may be available; the keys for such information should hopefully be fairly self-explanatory. To see what's available you can get a copy of the bundle and print its content, as in
ols y 0 x bundle b = $model print b
If gretl is built with MPI support, and the program is running in MPI mode, returns the 0-based "rank" or ID number of the current process. Otherwise returns –1.
If gretl is built with MPI support, and the program is running in MPI mode, returns the number of MPI processes currently running. Otherwise returns 0.
Returns the total number of coefficients estimated in the last model.
Returns the number of observations in the currently selected sample. Related: $tmax.
In the case of panel data the value returned is the number of pooled observations (number of units times number of observations per unit). If you want the time-series length of a panel use $pd, and the number of included units can be found as $nobs divided by $pd.
Returns a 2-vector: its first element is the number of seconds elapsed since 1970-01-01 00:00:00 +0000 (UTC, or Coordinated Universal Time), which is widely used in the computing world to represent the current time, and the second is the current date in ISO 8601 "basic" format, YYYYMMDD. The strftime function may be used to process the first element, and epochday may be used to process the second.
Returns the number of series in the dataset (including the constant). Since const is always present in any dataset a return value of 0 indicates that no dataset is in place. Note that if this accessor is used within a function, the number of series currently accessible may well fall short of that given by $nvars.
Applicable when the current dataset is time-series with annual, quarterly, monthly or decennial frequency, or is dated daily or weekly, or when the dataset is a panel with time-series information set appropriately (see the setobs command). The returned series holds 8-digit numbers on the pattern YYYYMMDD (ISO 8601 "basic" date format), which correspond to the day of the observation, or the first day of the observation period in case of a time-series frequency less than daily.
Such a series can be helpful when using the join command.
Returns a series holding the "major" or low-frequency component of each observation. This means the year for annual, quarterly or monthly time series; the day for hourly data; or the individual in the case of panel data. If the data are cross-sectional the series returned is just a 1-based index of the observations.
See also $obsminor, $obsmicro.
Applicable when the observations in the current dataset have a major:minor:micro structure, as in dated daily time series (year:month:day). Returns a series holding the micro or highest-frequency component of each observation (for example, the day).
See also $obsmajor, $obsminor.
Applicable when the observations in the current dataset have a major:minor structure, as in quarterly time series (year:quarter), monthly time series (year:month), hourly data (day:hour) and panel data (individual:period). Returns a series holding the minor or high-frequency component of each observation (for example, the month).
In the case of dated daily data, $obsminor gets the month of each observation.
See also $obsmajor, $obsmicro.
Specific to panel data, returns the time-series periodicity (e.g. 4 for quarterly data). If the periodicity is not set in the active panel dataset, returns 1 in analogy to $pd for cross-sectional or undated data. If the dataset is not a panel NA is returned.
See also $pd, $datatype, setobs.
Following estimation of a single-equation model, returns an array of strings holding the names of the model's parameters. The number of names matches the number of elements in the $coeff vector.
For models specified via a list of regressors the result will be the same as that of
varnames($xlist)
(see varnames), but $parnames is more general; it also works for models with no regressor list (nls, mle, gmm).
Returns the frequency or periodicity of the data (e.g. 4 for quarterly data). In the case of panel data the value returned is the total time-series length.
See also $panelpd.
Returns the value of π in double precision.
A special facility for use by authors of function packages. Returns an empty string unless a packaged function is executing, in which case it returns the full (platform dependent) path under which the package is installed. For instance the return value might be
/usr/share/gretl/functions/foo
if that's the directory in which foo.gfn is located. This enables package writers to access resources such as matrix files that they have included in their package.
Available after estimation of a vector autoregression. Returns a row vector holding the results of the multivariate portmanteau test for autocorrelation of the residuals, as discussed on pages 21–22 in Johansen (1995). The elements are, in order, the Ljung–Box statistic, the maximum lag considered, the degrees of freedom for the (chi-square) test, and the p-value of the test.
Returns the p-value of the test statistic that was generated by the last explicit hypothesis-testing command, if any (for example, chow). See chapter 10 of the Gretl User's Guide for details.
In most cases the return value is a scalar but sometimes it is a matrix (for example, the trace and lambda-max p-values from the Johansen cointegration test); in that case the values in the matrix are laid out in the same pattern as the printed results.
See also $test.
Must follow an invocation of the qlrtest command (the QLR test for a structural break at an unknown point). The value returned is the 1-based index of the observation at which the test statistic is maximized.
Provides stored information following certain commands that do not have specific accessors. The commands in question include bds, bkw, corr, fractint, freq, hurst, leverage, summary, vif and xtab (in which cases the result is a matrix), plus pkg (which optionally stores a bundle result).
| Argument: | n (scalar, optional) |
Without arguments, returns the first-order autoregressive coefficient for the residuals of the last model. After estimating a model via the ar command, the syntax $rho(n) returns the corresponding estimate of ρ(n).
Following estimation of a restricted VECM, returns the log-likelihood for the restricted model. See also $lnl, and chapter 33 of the Gretl User's Guide for examples of usage.
Returns the unadjusted R2 from the last estimated model, if available. Usually this will be the regular (centered) R2 but if the specification contains no constant (and no set of regressors that "add up to" a constant) it will be the uncentered version. In that case the centered version can be accessed as $model.centered_R2.
Must follow estimation of a single-equation model. Returns a dummy series with value 1 for observations used in estimation, 0 for observations within the currently defined sample range but not used (presumably because of missing values), and NA for observations outside of the current range.
If you wish to compute statistics based on the sample that was used for a given model, you can do, for example:
ols y 0 xlist series sdum = $sample smpl sdum --dummy
Must follow a tsls command. Returns a 1 x 3 vector, containing the value of the Sargan over-identification test statistic, the corresponding degrees of freedom and p-value, in that order. If the model is exactly identified, the statistic is unavailable, and trying to access it provokes an error.
Returns the value with which gretl's random number generator was seeded. If you set the seed yourself there's no need to use this accessor, but it may be of interest if the seed was set automatically (based on the time that execution of the program started).
Requires that a model has been estimated. If the last model was a single equation, returns the (scalar) Standard Error of the Regression (or in other words, the standard deviation of the residuals, with an appropriate degrees of freedom correction). If the last model was a system of equations, returns the cross-equation covariance matrix of the residuals.
| Argument: | s (name of coefficient, optional) |
With no arguments, $stderr returns a column vector containing the standard error of the coefficients for the last model. With the optional string argument it returns a scalar, namely the standard error of the parameter named s.
If the "model" in question is actually a system, the result depends on the characteristics of the system: for VARs and VECMs the value returned is a matrix with one column per equation, otherwise it is a column vector containing the coefficients from the first equation followed by those from the second equation, and so on.
Must be preceded by set stopwatch, which activates the measurement of CPU time. The first use of this accessor yields the seconds of CPU time that have elapsed since the set stopwatch command. At each access the clock is reset, so subsequent uses of $stopwatch yield the seconds of CPU time since the previous access.
When a user-defined function is executing, the set stopwatch command and $stopwatch accessor are specific to that function—that is, timing within a function does not disrupt any "global" timing that may be going on in the main script.
Must follow estimation of a simultaneous equations system. Returns the matrix of coefficients on the lagged endogenous variables, if any, in the structural form of the system. See the system command.
Must follow estimation of a simultaneous equations system. Returns the matrix of coefficients on the exogenous variables in the structural form of the system. See the system command.
Must follow estimation of a simultaneous equations system. Returns the matrix of coefficients on the contemporaneous endogenous variables in the structural form of the system. See the system command.
Returns a bundle containing information on the capabilities of the gretl build and the system on which gretl is running. The members of the bundle are as follows:
gui_mode: integer, equals 1 if libgretl is being called by the GUI program, otherwise 0.
mpi: integer, equals 1 if the system supports MPI (Message Passing Interface), otherwise 0.
omp: integer, equals 1 if gretl is built with support for Open MP, otherwise 0.
ncores: integer, the number of physical processor cores available.
nproc: integer, the number of processors available, which will be greater than ncores if hyper-threading is enabled.
mpimax: integer, the maximum number of MPI processes that can be run in parallel. This is zero if MPI is not supported, otherwise it equals the local nproc value unless an MPI hosts file has been specified, in which case it is the sum of the number of processors or "slots" across all the machines referenced in that file.
wordlen: integer, either 32 or 64 for 32- and 64-bit systems respectively.
os: string representing the operating system, either linux, macos, windows or other. Note that versions of gretl prior to 2021e gave the string osx for the Mac operating system; a version-independent test for Mac is therefore instring($sysinfo.os, "os")
hostname: the name of the host machine on which the current gretl process is running (with a fallback of localhost in case the name cannot be determined).
mem: a 2-vector holding total physical memory and free or available memory, expressed in MB. This information may not be available on all systems but should be on Windows, macOS and Linux.
blas: string identifying the supplier of the BLAS (Basic Linear Algebra Subprograms) library in use by gretl.
blas_version: string identifying the version number of the blas library in use.
blascore: (if applicable) a string identifying the CPU type for which the current blas library is optimized.
compiler: a string identifying the compiler used when building libgretl.
cpuid: a string identifying the vendor and model of the CPU on which libgretl is running.
gnuplot: a string identifying the version of gnuplot available to gretl for plotting, in the form of three dot-separated numbers giving major version, minor version and patchlevel.
foreign: a sub-bundle containing 0/1 indicators for the presence on the host system of each of the "foreign" programs supported by gretl, under the keys julia, octave, ox, python, Rbin, Rlib and stata. The two keys pertaining to R represent the R executable and shared library, respectively.
Note that individual elements in the bundle can be accessed using "dot" notation without any need to copy the whole bundle under a user-specified name. For example,
if $sysinfo.os == "linux" # do something linux-specific endif
Must follow estimation of a system of equations via one of the commands system, var or vecm; returns a bundle containing many items of data pertaining to the system. All the relevant regular system accessors are included: these are referenced by keys that are the same as the regular accessor names, minus the leading dollar sign. So for example the residuals appear under the key uhat and the coefficients under coeff. (Exceptions are the keys A, B, and Gamma, which correspond to the regular dollar accessors sysA, sysB, and sysGamma.) The keys for additional information should hopefully be fairly self-explanatory. To see what's available you can get a copy of the bundle and print its content, as in
var 4 y1 y2 y2 bundle b = $system print b
A bundle obtained in this way can be passed as the final, optional argument to the functions fevd and irf.
Returns the number of observations used in estimating the last model.
Returns the 1-based index of the first observation in the currently selected sample.
Returns the 1-based index of the last observation in the currently selected sample.
Returns the value of the test statistic that was generated by the last explicit hypothesis-testing command, if any (e.g. chow). See chapter 10 of the Gretl User's Guide for details.
In most cases the return value is a scalar but sometimes it is a matrix (for example, the trace and lambda-max statistics from the Johansen cointegration test); in that case the values in the matrix are laid out in the same pattern as the printed results.
See also $pvalue.
For time-series or panel data, creates a 1-based index of the time period. In the panel case the sequence of values repeats for each cross-sectional unit.
The command "genr time" is an alternative, with the difference that the genr variant automatically creates a series called time while the naming of the series is up to the caller when using $time, as in
series trend = $time
This accessor is not available for cross-sectional data.
Returns the maximum legal setting for the end of the sample range via the smpl command. In most cases this will equal the number of observations in the dataset but within a hansl function the $tmax value may be smaller, since in general data access within functions is limited to the sample range set by the caller.
Note that $tmax does not in general equal $nobs, which gives the number of observations in the current sample range.
Returns TR2 (sample size times R-squared) from the last model, if available.
Returns the residuals from the last model. This may have different meanings for different estimators. For example, after an ARMA estimation $uhat will contain the one-step-ahead forecast error; after a probit model, it will contain the generalized residuals.
If the "model" in question is actually a system (a VAR or VECM, or system of simultaneous equations), $uhat retrieves the matrix of residuals, one column per equation.
Valid for panel datasets only. Returns a series with value 1 for all observations on the first unit or group, 2 for observations on the second unit, and so on.
| Arguments: | s1 (name of coefficient, optional) |
| s2 (name of coefficient, optional) |
With no arguments, $vcv returns a square matrix containing the estimated covariance matrix for the coefficients of the last model. If the last model was a single equation, then you may supply the names of two parameters in parentheses to retrieve the estimated covariance between the parameters named s1 and s2. See also $coeff, $stderr.
This accessor is not available for VARs or VECMs; for models of that sort see $sigma and $xtxinv.
Must follow the estimation of a VECM; returns a matrix in which the Gamma matrices (coefficients on the lagged differences of the cointegrated variables) are stacked side by side. Each row represents an equation; for a VECM of lag order p there are p – 1 sub-matrices.
Returns an integer value that codes for the program version. The current gretl version string takes the form of a 4-digit year followed by a letter from a to j representing the sequence of releases within the year (for example, 2015d). The return value from this accessor is formed as 10 times the year plus the zero-based lexical order of the letter, so 2015d translates to 20153.
Prior to gretl 2015d, version identifiers took the form x.y.z (three integers separated by dots), and in that case the accessor value was calculated as 10000*x + 100*y + z, so that for example 1.10.2 (the last release under the old scheme) translates as 11002. Numerical order of $version values is therefore preserved across the change in versioning scheme.
Must follow the estimation of a VAR or a VECM; returns a matrix containing the VMA representation up to the order specified via the set horizon command. See chapter 32 of the Gretl User's Guide for details.
Returns 1 if gretl is running on MS Windows, otherwise 0. By conditioning on the value of this variable you can write shell calls that are portable across different operating systems.
Also see the shell command.
If the last model was a single equation, returns the list of regressors. If the last model was a system of equations, returns the "global" list of exogenous variables (in the same order in which they appear in $sysB). If the last model was a VAR, returns the list of exogenous regressors, if any, except for standard deterministic terms (constant, trend, seasonals).
Following estimation of a VAR or VECM (only), returns X'X-1, where X is the common matrix of regressors used in each of the equations. While this accessor is available for a VECM estimated with a restriction imposed on α (the "loadings" matrix), it should be borne in mind that in that case not all coefficients of the regressors are freely varying.
Returns the fitted values from the last regression.
If the last model estimated was a VAR, VECM or simultaneous system, returns the associated list of endogenous variables. If the last model was a single equation, this accessor gives a list with a single element, the dependent variable. In the special case of the biprobit model the list contains two elements.
Yields the full path of the directory gretl uses for temporary files. To use it in string-substitution mode, prepend the at-sign (@dotdir).
Yields the path to the gnuplot executable. To use it in string-substitution mode, prepend the at-sign (@gnuplot).
Yields the full path of the gretl installation directory. To use it in string-substitution mode, prepend the at-sign (@gretldir).
Returns a string representing the national language in force currently, if this can be determined. The string is composed of a two-letter ISO 639-1 language code (for example, en for English, jp for Japanese, el for Greek) followed by an underscore plus a two-letter ISO 3166-1 country code. Thus for example Portuguese in Portugal gives pt_PT while Portuguese in Brazil gives pt_BR.
If the national language cannot be determined, the string "unknown" is returned.
Yields the path to the seats executable, which accompanies tramo. To use it in string-substitution mode, prepend the at-sign (@seats).
Yields the path to the tramo executable. To use it in string-substitution mode, prepend the at-sign (@tramo).
Yields the path string of the tramo data directory. To use it in string-substitution mode, prepend the at-sign (@tramodir).
Yields the path which gretl reads from and writes to by default. A fuller discussion is provided in the Command Reference under workdir. Note that this string can be set by the user via the set command. To use it in string-substitution mode, prepend the at-sign (@workdir).
Yields the path to the x-12-arima (or x-13arima) executable. To use it in string-substitution mode, prepend the at-sign (@x12a).
Yields the path of the x-12-arima (or x-13arima) data directory. To use it in string-substitution mode, prepend the at-sign (@x12adir).
| Argument: | x (scalar, series or matrix) |
Returns the absolute value of x.
| Argument: | x (scalar, series or matrix) |
Returns the arc cosine of x, that is, the value whose cosine is x. The result is in radians; the input should be in the range –1 to 1.
| Argument: | x (scalar, series or matrix) |
Returns the inverse hyperbolic cosine of x (positive solution). x should be greater than 1; otherwise, NA is returned. See also cosh.
| Arguments: | x (series, list or matrix) |
| byvar (series, list or matrix) | |
| funcname (string, optional) |
Most of the following assumes that the first two arguments to this function take the form of series or lists, but see "Matrix input" below for alternative usage.
In the simplest usage x is set to null, byvar is a single series and the third argument is omitted or set to null. The return value is then a matrix with two columns holding, respectively, the distinct values of byvar sorted in ascending order, and the count of observations at which byvar takes on each of these values. For example,
open data4-1 eval aggregate(null, bedrms)
will show that the series bedrms has values 3 (with count 5) and 4 (with count 9).
More generally, if byvar is a list with n members then the first n columns of the returned matrix hold the combinations of the distinct values of each of the n series, and the count column holds the number of observations at which each combination is realized. (The count column can always be found at the position nelem(byvar)+1).
If the third argument is given then x must not be null, and the rightmost m columns hold the values of the statistic specified by funcname for each of the variables in x. (So m is equal to 1 if x is a single series and equal to nelem(x) if x is a list.) The specified statistic is calculated on the sub-samples defined by the combinations in byvar (in ascending order); these combinations are shown in the first n column(s) of the returned matrix.
So, if both x and byvar are individual series, the return value is a matrix with three columns holding the distinct values of byvar sorted in ascending order; the count of observations at which byvar takes on each of these values; and the values of the statistic specified by funcname calculated on series x, using just those observations at which byvar takes on the value given in the first column.
The following values of funcname are supported "natively": sum, sumall, mean, sd, var, sst, skewness, kurtosis, min, max, median, nobs, gini, isconst and isdummy. Each of these functions takes a series argument and returns a scalar value, and in that sense can be said to "aggregate" the series in some way. If none of these built-in functions does what you need, you can give the name of a user-defined function as the aggregator. Like the built-ins, such a function must take a single series argument and return a scalar value.
Note that although a count of cases is provided automatically the nobs function is not redundant as an aggregator, since it gives the number of valid (non-missing) observations on x at each byvar combination.
First, suppose that region represents a coding of geographical region using integer values 1 to n, and income represents household income. Then the following would produce an n x 3 matrix holding the region codes, the count of observations in each region, and mean household income for each of the regions:
matrix m = aggregate(income, region, mean)
For an example using lists, let gender be a male/female dummy variable, let race be a categorical variable with three values, and consider the following:
list BY = gender race list X = income age matrix m = aggregate(X, BY, sd)
The aggregate call here will produce a 6 x 5 matrix. The first two columns hold the 6 distinct combinations of gender and race values; the middle column holds the count for each of these combinations; and the rightmost two columns contain the sample standard deviations of income and age.
If byvar is a list, some combinations of the byvar values may not be present in the data (giving a count of zero). In that case the value of the statistics for x are recorded as NaN (not a number). To cut out such cases you can use the selifr function to select only those rows that have a non-zero count. The column to test is one place to the right of the number of byvar variables, so we can do:
matrix m = aggregate(X, BY, sd) scalar c = nelem(BY) m = selifr(m, m[,c+1])
Instead of series or lists, x and byvar may be given in matrix form. However, if both arguments are provided they must match in type (you cannot give a series or list for one argument and a matrix for the other) and two matrix arguments must have the same number of rows. In this context matrix columns are treated as if they were series, so the aggregation function must follow the pattern described above, taking a series argument and returning a scalar.
| Arguments: | s (string) |
| default (string, optional) |
For s the name of a parameter to a user-defined function, returns the name of the corresponding argument, if the argument had a name at the caller level. If the argument was anonymous, an empty string is returned unless the optional default argument is provided, in which case its value is used as a fallback.
| Argument: | n (integer) |
The basic "constructor" function for a new array variable. In using this function you must specify a type (in plural form) for the array: strings, matrices, bundles, lists or arrays. The return value is an array of the specified type with n elements, each of which is initialized as "empty" (e.g. zero-length string, null matrix). Examples of usage:
strings S = array(5) matrices M = array(3)
See also defarray.
| Argument: | x (scalar, series or matrix) |
Returns the arc sine of x, that is, the value whose sine is x. The result is in radians; the input should be in the range –1 to 1.
| Argument: | x (scalar, series or matrix) |
Returns the inverse hyperbolic sine of x. See also sinh.
| Arguments: | a (array) |
| fname (string) |
Performs an in-place sort of the elements of a, using a comparator function specified by the caller under the control of the quicksort routine.
The argument a can be of any of the types supported for a gretl array, namely strings, matrices, bundles, lists or arrays. The fname argument must be the name of a function which takes two const arguments, whose type matches that of the elements of a. This function must return an integer value on the following pattern: 0 if the two arguments have the same sort order, negative if the first argument sorts before the second, or positive if the second sorts before the first. (The exact values do not matter.)
For example, suppose one wants to sort an array of bundles, each of which contains a scalar named crit, by increasing value of crit. Then the following function would be suitable for passing to asort:
function scalar my_bsort (const bundle b1, const bundle b2) return sgn(b1.crit - b2.crit) end function
If you want to preserve the unsorted array, make a copy of it before passing it to asort. The return value from this function is a nominal 0 on success.
See also sort for simple sorting of an array of strings.
| Argument: | expr (scalar) |
This function is intended for testing or debugging of hansl code. The argument should be an expression which evaluates to a scalar. The return value is 1 if expr evaluates to a non-zero value (boolean "true", or "success") or 0 if it evaluates to zero (boolean "false", or "failure").
By default there are no consequences of a call to assert failing other than the return value being zero. However, the set command can be used to make failure of an assertion more consequential. There are three levels:
# print a warning message but continue execution set assert warn # print an error message and stop script execution set assert stop # print a message to stderr and abort the program set assert fatal
In most cases stop is sufficient to terminate a script but in certain special cases (such as within a function called from a command block such as mle) it may be necessary to use the fatal setting to get a clear indication of the failing assertion. Note, however, that in this case the message will go to standard error output.
The default behavior can be restored via
set assert off
By way of a simple example, if at a certain point in a hansl script a scalar x ought to be non-negative, the following will flag an error if that is not the case:
set assert stop assert(x >= 0)
| Argument: | x (scalar, series or matrix) |
Returns the arc tangent of x, that is, the value whose tangent is x. The result is in radians.
| Arguments: | y (scalar, series or matrix) |
| x (scalar, series or matrix) |
Returns the principal value of the arc tangent of y/x, using the signs of the two arguments to determine the quadrant of the result. The return value is in radians, in the range [–π, π].
If the two arguments differ in type, the type of the result is the "higher" of the two, where the ordering is matrix > series > scalar. For example, if y is a scalar and x an n-vector (or vice versa) the result is an n-vector. Note that matrix arguments must be vectors, and if neither argument is a scalar the two arguments must be of the same length.
| Argument: | x (scalar, series or matrix) |
Returns the inverse hyperbolic tangent of x. See also tanh.
| Argument: | s (string) |
Closely related to the C library function of the same name. Returns the result of converting the string s (or the leading portion thereof, after discarding any initial white space) to a floating-point number. Unlike atof in C, however, the decimal character is always assumed (for reasons of portability) to be ".". Any characters that follow the portion of s that converts to a floating-point number under this assumption are ignored.
If none of s (following any discarded white space) is convertible under the stated assumption, NA is returned.
# examples
x = atof("1.234") # gives x = 1.234
x = atof("1,234") # gives x = 1
x = atof("1.2y") # gives x = 1.2
x = atof("y") # gives x = NA
x = atof(",234") # gives x = NA
See also sscanf for more flexible string to numeric conversion.
| Arguments: | target (reference to bundle) |
| input (bundle, optional) | |
| required-keys (array of strings, optional) |
Primarily intended for use by writers of function packages. Here is the context in which bcheck may be useful: you have a function which accepts a bundle argument whereby the caller can make various choices. Some elements of the bundle may have default values—so the caller is not obliged to make an explicit choice—while other elements may be required. You want to determine whether the argument you get is valid. The main text below assumes that an input bundle is supplied by the caller of your function, but see the section headed "No input bundle" for the contrary case.
To use bcheck you construct a template bundle containing all the supported keys, with values that exemplify the type associated with each key, and pass this in pointer form as target. For the second argument, input, pass the bundle you get from the caller. This function then checks the following:
Does input contain any keys not present in target? If so, bcheck returns a non-zero value, indicating that input is erroneous. (Most likely, the key in question is misspelled.)
Does input contain under any given key an object whose type does not match that in target? If so, a non-zero value is returned.
If some elements in target require input from the caller (so the value you supply is not a default value, just a placeholder to indicate the required type), you should supply a third argument to bcheck: an array of strings holding the keys for which input is not optional. Then the return value will be non-zero if any required elements are missing from input.
In addition to the above you may wish to impose lower and/or upper bounds on the value of one or more scalar members of the bundle argument. If so, add a bundle named bounds to your template bundle. Each member of this secondary bundle should have a key that identifies a member of the template bundle; its value should be a 2-vector holding lower and upper limits. Put NA in place of one of the limits if it is unbounded. So, for example, the following code will check that if x1 is given in the caller's input it is between 1 and 5, and if x2 is given it is non-negative:
template.bounds = _(x1={1,5}, x2={0,NA})
If no errors are detected on any of these points, values supplied in input are copied to target (defaults being replaced by valid selections on the caller's part). If errors are found a message will be printed indicating what is wrong with input.
To give a simple example, suppose your function's argument bundle supports a matrix X (required), a non-negative scalar z with default value 0, and a string s with default value "display". Then the following code fragment would be suitable for checking a bundle named uservals supplied by the caller:
bundle target = _(X={}, z=0, s="display")
target.bounds = _(z={0,NA})
strings req = defarray("X")
err = bcheck(&target, uservals, req)
if err
# react appropriately
else
# proceed, using the values in target
endif
If the input bundle is not supplied to bcheck, it behaves as follows. If the required-keys argument is not given, it returns zero (since none of the error conditions mentioned above can occur), and target is not modified. Otherwise it returns non-zero since it's clear that one or more specifications must be missing. This means that it's safe to pass a null input to bcheck.
| Arguments: | type (character) |
| v (scalar) | |
| x (scalar, series or matrix) |
Computes one of the Bessel function variants for order v and argument x. The return value is of the same type as x. The specific function is selected by the first argument, which must be J, Y, I, or K. A good discussion of the Bessel functions can be found on Wikipedia; here we give a brief account.
case J: Bessel function of the first kind. Resembles a damped sine wave. Defined for real v and x, but if x is negative then v must be an integer.
case Y: Bessel function of the second kind. Defined for real v and x but has a singularity at x = 0.
case I: Modified Bessel function of the first kind. An exponentially growing function. Acceptable arguments are as for case J.
case K: Modified Bessel function of the second kind. An exponentially decaying function. Diverges at x = 0 and is not defined for negative x. Symmetric around v = 0.
| Arguments: | &b (reference to matrix) |
| f (function call) | |
| g (function call, optional) |
Numerical maximization via the method of Broyden, Fletcher, Goldfarb and Shanno. On input the vector b should hold the initial values of a set of parameters, and the argument f should specify a call to a function that calculates the (scalar) criterion to be maximized, given the current parameter values and any other relevant data. If the object is in fact minimization, this function should return the negative of the criterion. On successful completion, BFGSmax returns the maximized value of the criterion, and b holds the parameter values which produce the maximum.
The optional third argument provides a means of supplying analytical derivatives (otherwise the gradient is computed numerically). The gradient function call g must have as its first argument a predefined matrix that is of the correct size to contain the gradient, given in pointer form. It also must take the parameter vector as an argument (in pointer form or otherwise). Other arguments are optional.
For more details and examples see chapter 37 of the Gretl User's Guide. See also BFGScmax, NRmax, fdjac, simann.
An alias for BFGSmax; if called under this name the function acts as a minimizer.
| Arguments: | &b (reference to matrix) |
| bounds (matrix) | |
| f (function call) | |
| g (function call, optional) |
Constrained numerical maximization using L-BFGS-B (limited memory BFGS, see Byrd, Lu, Nocedal and Zhu, 1995). On input the vector b should hold the initial values of a set of parameters, bounds should hold bounds on the parameter values (see below), and f should specify a call to a function that calculates the (scalar) criterion to be maximized, given the current parameter values and any other relevant data. If the object is in fact minimization, this function should return the negative of the criterion. On successful completion, BFGScmax returns the maximized value of the criterion, subject to the constraints in bounds, and b holds the parameter values which produce the maximum.
The bounds matrix must have 3 columns and as many rows as there are constrained elements in the parameter vector. The first element on a given row is the (1-based) index of the constrained parameter; the second and third are the lower and upper bounds, respectively. The values -$huge and $huge should be used to indicate that the parameter is unconstrained downward or upward, respectively. For example, the following is the way to specify that the second element of the parameter vector must be non-negative:
matrix bounds = {2, 0, $huge}
The optional fourth argument provides a means of supplying analytical derivatives (otherwise the gradient is computed numerically). The gradient function call g must have as its first argument a predefined matrix that is of the correct size to contain the gradient, given in pointer form. It also must take the parameter vector as an argument (in pointer form or otherwise). Other arguments are optional.
For more details and examples see chapter 37 of the Gretl User's Guide. See also BFGSmax, NRmax, fdjac, simann.
An alias for BFGScmax; if called under this name the function acts as a minimizer.
| Argument: | B (matrix) |
Given a matrix B containing only zeros and ones, this function interprets each row as the binary representation of a 32-bit unsigned integer, and returns a column vector with the decimal representation of those integers. The argument cannot have more than 32 columns otherwise an error is flagged.
Note that the least significant bit comes in the first column. So column 1 corresponds to 20, column 2 to 21, and so on. For example, the expression
scalar x = bin2dec({1,0,1})
stores the value 5 into x.
The dec2bin function performs the inverse transformation.
| Arguments: | n (scalar, series or matrix) |
| k (scalar, series or matrix) |
Returns the binomial coefficient, that is the number of ways in which k items can be chosen from n items without repetition, irrespective of ordering. This is also equal to the coefficient of the (k+1)-th term in the polynomial expansion of the binomial power (1+x)^n.
For integer arguments the result is n!/(k!(n-k)!) but the function also accepts noninteger arguments, and the formula above generalizes to Γ(n+1)/(Γ(k+1) × Γ(n-k+1)).
When k > n or k < 0 no valid answer exists and an error is flagged.
If the two arguments differ in type, the type of the result is the "higher" of the two, where the ordering is matrix > series > scalar. For example, if n is a scalar and k an r-vector (or vice versa) the result is an r-vector. Note that matrix arguments must be vectors, and if neither argument is a scalar the two arguments must be of the same length.
See also gammafun and lngamma.
| Arguments: | n (integer) |
| k (integer) |
Binary permutations: returns a p x n matrix, each of whose rows holds a distinct arrangement of k ones and n – k zeros (in lexicographic order). The maximum supported value of n is 64, n and k must be non-negative, and k must be no greater than n; otherwise an error is flagged. In case n = k = 0 an empty matrix is returned.
For example, with n = 4 and k = 2, the result is
0 0 1 1 0 1 0 1 0 1 1 0 1 0 0 1 1 0 1 0 1 1 0 0
Warning: the number of permutations, p, is a steeply increasing function of n and is greatest when k is about half of n. You may want to check in advance the size of the matrix that binperms will attempt to allocate. The bincoeff function returns p, and the size of the resulting matrix in megabytes can be calculated as
MB = 8 * n * bincoeff(n, k) / 10^6
For n = 30, this gives about 34 MB when k = 25, 7211 MB if k = 20, and 20758 MB if k = 18.
| Arguments: | y (series) |
| f1 (integer, optional) | |
| f2 (integer, optional) | |
| k (integer, optional) |
Returns the result from application of the Baxter–King bandpass filter to the series y. The optional parameters f1 and f2 represent, respectively, the lower and upper bounds of the range of frequencies to extract, while k is the approximation order to be used.
If these arguments are not supplied then the default values depend on the periodicity of the dataset. For yearly data the defaults for f1, f2 and k are 2, 8 and 3, respectively; for quarterly data, 6, 32 and 12; for monthly data, 18, 96 and 36. These values are chosen to match the most common choice among practitioners, that is to use this filter for extracting the "business cycle" frequency component; this, in turn, is commonly defined as being between 18 months and 8 years. The filter, per default choice, spans 3 years of data.
If f2 is greater than or equal to the number of available observations, then the "low-pass" version of the filter will be run and the resulting series should be taken as an estimate of the trend component, rather than the cycle. See also bwfilt, hpfilt.
| Arguments: | V (matrix) |
| parnames (array of strings, optional) | |
| verbose (boolean, optional) |
Computes BKW collinearity diagnostics (see Belsley, Kuh and Welsch (1980)) given a covariance matrix of parameter estimates, V. The optional second argument, which can be an array of strings or a string containing comma-separated names, is used to label the columns showing the variance proportions; the number of names should match the dimension of V. After estimation of a model in gretl, suitable arguments can be obtained via the $vcv and $parnames accessors.
By default this function operates silently, just returning the BKW table as a matrix, but if a non-zero value is given for the third argument the table is printed along with some analysis.
There is also a command form of this facility, bkw, which automatically references the last model and requires no arguments.
| Arguments: | y (series or matrix) |
| d (scalar) |
Returns the Box–Cox transformation with parameter d for the positive series y (or the columns of matrix y).
The result is (yd - 1)/d for d not equal to zero, or log(y) for d = 0.
| Arguments: | fname (string) |
| import (boolean, optional) |
Reads a bundle from the file specified by the fname argument. By default the bundle is assumed to be represented in XML, and to be gzip-compressed if fname has extension .gz. But if the extension is .json or .geojson the content is assumed to be JSON.
In the XML case the file must contain a gretl-bundle element, which is used to store zero or more bundled-item elements. For example,
moo 3
As you might expect, files suitable for reading via bread are generated by the companion function bwrite.
If the file name does not contain a full path specification, it will be looked for in several "likely" locations, beginning with the currently set workdir. However, if a non-zero value is given for the optional import argument, the input file is taken to be in the user's "dot" directory. In that case fname should be a plain file name, without any path component.
Should an error occur (such as the file being badly formatted or inaccessible), an error is returned via the $error accessor.
| Arguments: | B (bundle) |
| oldkey (string) | |
| newkey (string) |
If the bundle B contains a member under the key oldkey, its key is changed to newkey, otherwise an error is flagged. Returns 0 on successful renaming.
Changing the key of a bundle member is not a common task but it can arise in the context of functions that work with bundles, and brename is an efficient tool for the job. Example:
# set up a bundle holding a big matrix bundle b b.X = mnormal(1000, 1000) if 0 # change the key manually Xcopy = b.X delete b.X b.Y = Xcopy delete Xcopy else # versus: change it efficiently brename(b, "X", "Y") endif
The first method requires that the big matrix be copied twice, out of the bundle then back into it under a different key; the efficient method changes the key directly.
| Arguments: | y (series) |
| n (integer) | |
| omega (scalar) |
Returns the result from application of a low-pass Butterworth filter with order n and frequency cutoff omega to the series y. The cutoff is expressed in degrees and must be greater than 0 and less than 180. Smaller cutoff values restrict the pass-band to lower frequencies and hence produce a smoother trend. Higher values of n produce a sharper cutoff, at the cost of possible numerical instability.
Inspecting the periodogram of the target series is a useful preliminary when you wish to apply this function. See chapter 30 of the Gretl User's Guide for details. See also bkfilt, hpfilt.
| Arguments: | B (bundle) |
| fname (string) | |
| export (boolean, optional) |
Writes the bundle B to file, serialized in XML or, if fname has extension .json or .geojson, as JSON. See bread for a description of the format when XML is used. If fname already exists, it will be overwritten. The nominal return value is 0 on successful completion; if writing fails an error is flagged.
The output file will be written in the currently set workdir, unless fname contains a full path specification. However, if a non-zero value is given for the export argument, the file will be written into the user's "dot" directory. In that case a plain file name, without any path component, should be given for the second argument.
In the case of XML output (only), the option of gzip compression is available; this is applied if fname has the extension .gz.
| Argument: | C (complex matrix) |
Returns an m x n real matrix holding the complex "argument" of each element of the m x n complex matrix C. The argument of the complex number z = x + yi can also be computed as atan2(y, x).
| Arguments: | X (matrix) |
| standardize (boolean, optional) | |
| skip_na (boolean, optional) |
Centers the columns of matrix X around their means. If the optional second argument has a non-zero value then in addition the centered values are divided by the column standard deviations (which are calculated using n – 1 as divisor, where n is the number of rows of X).
If a non-zero value is supplied for skip_na missing values are ignored, otherwise if a column of X contains any missing values the corresponding column in the output is all missing.
Note that stdize provides more flexible functionality.
| Arguments: | d (string) |
| ... (see below) | |
| x (scalar, series or matrix) |
Cumulative distribution function calculator. Returns P(X <= x), where the distribution of X is determined by the string d. Between the arguments d and x, zero or more additional scalar arguments are required to specify the parameters of the distribution, as follows (but note that the normal distribution has its own convenience function, cnorm).
Standard normal (d = z, n, or N): no extra arguments
Bivariate normal (D): correlation coefficient
Logistic (lgt or s): no extra arguments
Student's t (t): degrees of freedom
Chi square (c, x, or X): degrees of freedom
Snedecor's F (f or F): df (num.); df (den.)
Gamma (g or G): shape; scale
Beta (beta): 2 shape parameters
Binomial (b or B): probability; number of trials
Poisson (p or P): mean
Exponential (exp): scale
Weibull (w or W): shape; scale
Laplace (l or L): mean; scale
Generalized Error (E): shape
Non-central chi square (ncX): df, non-centrality parameter
Non-central F (ncF): df (num.), df (den.), non-centrality parameter
Non-central t (nct): df, non-centrality parameter
Note that most cases have aliases to help memorizing the codes. The bivariate normal case is special: the syntax is x = cdf(D, rho, z1, z2) where rho is the correlation between the variables z1 and z2.
See also pdf, critical, invcdf, pvalue.
| Arguments: | X (matrix) |
| Y (matrix) |
This is a legacy function, predating gretl's native support for complex matrices.
Complex division. The two arguments must have the same number of rows, n, and either one or two columns. The first column contains the real part and the second (if present) the imaginary part. The return value is an n x 2 matrix or, if the result has no imaginary part, an n-vector. See also cmult.
| Argument: | L (list) |
This function returns a list in which each series in L that has the "coded" attribute is replaced by a set of dummy variables representing each of its coded values, with the least value omitted. If L contains no coded series the return value will be identical to L.
The generated dummy variables, if any, are named on the pattern Dvarname_vi where vi is the ith represented value of the coded variable. In case any values are negative, "m" is inserted before the (absolute) value of vi.
For example, suppose L contains a coded series named C1 with values –9, –7, 0, 1 and 2. Then the generated dummies will be DC1_m7 (coding for C1 = –7), DC1_0 (coding for C1 = 0), and so on.
| Argument: | x (scalar, series or matrix) |
Ceiling function: returns the smallest integer greater than or equal to x. See also floor, int.
| Argument: | A (positive definite matrix) |
Performs a Cholesky decomposition of A. If A is real it must be symmetric and positive definite; if so, the result is a lower-triangular matrix L which satisfies A = LL'. If A is complex it must be Hermitian and positive definite, and the result is a lower-triangular complex matrix such that A = LL^H. Otherwise, the function will return an error.
For the real case, see also psdroot and Lsolve.
| Arguments: | Y (matrix) |
| xfac (integer) | |
| X (matrix, optional) |
We no longer recommend use of this function; please use tdisagg instead.
Expands the input data, Y, to a higher frequency, using the method of Chow and Lin (1971). It is assumed that the columns of Y represent data series; the returned matrix has as many columns as Y and xfac times as many rows. It is also assumed that each low-frequency value should be treated as the average of xfac high-frequency values.
The xfac value should be 3 for quarterly to monthly, 4 for annual to quarterly or 12 for annual to monthly. The optional third argument may be used to provide a matrix of covariates at the higher (target) frequency.
The regressors used by default are a constant and trend. If X is provided, its columns are used as additional regressors; it is an error if the number of rows in X does not equal xfac times the number of rows in Y.
| Argument: | C (complex matrix) |
Returns an m x n real matrix holding the complex modulus of each element of the m x n complex matrix C. The modulus of the complex number z = x + yi equals the square root of x2 + y2.
| Arguments: | X (matrix) |
| Y (matrix) |
This is a legacy function, predating gretl's native support for complex matrices.
Complex multiplication. The two arguments must have the same number of rows, n, and either one or two columns. The first column contains the real part and the second (if present) the imaginary part. The return value is an n x 2 matrix, or, if the result has no imaginary part, an n-vector. See also cdiv.
| Argument: | x (scalar, series or matrix) |
Returns the cumulative distribution function for a standard normal. See also dnorm, qnorm.
| Argument: | X (matrix) |
Returns the condition number of the n x k matrix X, as defined in Belsley, Kuh and Welsch (1980). If the columns of X are mutually orthogonal the condition number of X is unity. Conversely, a large value of the condition number is an indicator of multicollinearity; "large" is often taken to mean 50 or greater (sometimes 30 or greater).
The steps in the calculation are: (1) form a matrix Z whose columns are the columns of X divided by their respective Euclidean norms; (2) form Z'Z and obtain its eigenvalues; and (3) compute the square root of the ratio of the largest to the smallest eigenvalue.
See also rcond.
| Arguments: | M (matrix) |
| col (integer, optional) |
If the col argument is given, retrieves the name for column col of matrix M. If M has no column names attached the value returned is an empty string; if col is out of bounds for the given matrix an error is flagged.
If no second argument is given, retrieves an array of strings holding the column names from M, or an empty array if M does not have column names attached.
Example:
matrix A = { 11, 23, 13 ; 54, 15, 46 }
cnameset(A, "Col_A Col_B Col_C")
string name = cnameget(A, 3)
print name
See also cnameset.
| Arguments: | M (matrix) |
| S (array of strings or list) |
Attaches names to the columns of the T x k matrix M. If S is a named list, the names are taken from the names of the listed series; the list must have k members. If S is an array of strings, it should contain k elements. A single string is also acceptable as the second argument; in that case it should contain k space-separated substrings. As a special case, passing an empty string as the second argument has the effect of removing any existing column names.
The nominal return value is 0 on successful completion; in case of failure an error is flagged. See also rnameset.
Example:
matrix M = {1, 2; 2, 1; 4, 1}
strings S = array(2)
S[1] = "Col1"
S[2] = "Col2"
cnameset(M, S)
print M
| Argument: | X (matrix) |
Returns the number of columns of X. See also mshape, rows, unvech, vec, vech.
| Arguments: | A (matrix) |
| m (integer) | |
| n (integer, optional) | |
| post (integer, optional) | |
| add_id (integer, optional) |
Returns the matrix A premultiplied by the commutation matrix Km,n (using an algorithm that is more efficient than explicit multiplication). Each column of A is assumed to come from a vec operation on a m x n matrix. In particular,
commute(vec(B), rows(B), cols(B))
gives vec(B'). In order to compute the commutation matrix proper, just apply the function to an appropriately sized identity matrix. For example:
K_32 = commute(I(6), 3, 2)
The optional argument n defaults to m. If the optional argument post is non-zero, then post-multiplication is performed instead of pre-multiplication; the optional Boolean switch add_id will premultiply A by I + Km,n instead of Km,n.
| Arguments: | A (scalar or matrix) |
| B (scalar or matrix, optional) |
Returns a complex matrix, where A is taken to supply the real part and B the imaginary part. If A is m x n and B is a scalar the result is m x n with a constant imaginary part—and similarly in the converse case but with a constant real part. If both arguments are matrices they must be of the same dimensions. If the second argument is omitted the imaginary part defaults to zero. See also cswitch.
| Argument: | C (complex matrix) |
Returns an m x n complex matrix holding the complex conjugate of each element of the m x n complex matrix C. The conjugate of the complex number z = x + yi equals x – yi.
| Arguments: | x (scalar, series or matrix) |
| S (matrix) |
Provides a means of determining whether the numerical object x contains any of the elements of S, a matrix which plays the role of a set.
The return value is an object of the same size as x containing 1s in positions where a value of x matches any element of S and zeros elsewhere. For example, the code
matrix A = mshape(seq(1,9), 3, 3)
matrix C = contains(A, {1, 5, 9})
gives
A (3 x 3) 1 4 7 2 5 8 3 6 9 C (3 x 3) 1 0 0 0 1 0 0 0 1
This function may be particularly useful when x is a series that contains a fine-grained encoding for a qualitative characteristic, and you wish to reduce this to a smaller number of categories. You can pack into S a set of values to be consolidated, and obtain a dummy variable with value 1 for observations matching this set, 0 otherwise.
Since S serves as a set, for greatest efficiency it should be a vector with no repeated values, however an arbitrary matrix is accepted.
| Arguments: | A (matrix) |
| B (matrix) |
Computes the 2-dimensional convolution of the matrices A and B. If A is r x c and B is m x n then the returned matrix will have r+m-1 rows and c+n-1 columns.
| Argument: | Z (matrix) |
Given an m x n complex matrix Z, returns an m x n real matrix holding the quadrance of the elements of Z. The quadrance of the complex number z = a + bi is a2 + b2. It therefore equals the squared modulus of z and also equals z multiplied by its complex conjugate, but the direct calculation carried out by cquad is considerably faster than either of the alternative approaches.
| Arguments: | y1 (series or vector) |
| y2 (series or vector) |
Computes the correlation coefficient between y1 and y2. The arguments should be either two series, or two vectors of the same length. See also cov, mcov, mcorr, npcorr.
| Arguments: | a (series or vector) |
| b (series or vector) |
On the basis of a cross-tabulation of a and b, returns an integer code indicating the sort of correspondence between the two variables, as follows.
Code = 2: there’s a 1-to-1 relationship.
Code = 1: there’s a 1-to-n relationship (a "nests" b, can be interpreted as a function of b in the mathematical sense).
Code = –1: there’s an n-to-1 relationship (b "nests" a, can be interpreted as a function of a).
Code = 0: there’s no relationship.
Note that these codes are based solely on the sample values of the two arguments. In case b is the square of a, for example, the result will differ depending on whether a contains some pairs of values that differ only by sign (code = –1), or not (code = 2).
One possible use case is to check whether two discrete series encode the same information. For example, the following:
open grunfeld.gdt c = corresp($unit, firm)
gives c = 2, indicating that the series firm is in fact a unique identifier for the cross-sectional units in this panel dataset.
See also mxtab.
| Arguments: | x (series, matrix or list) |
| p (integer) | |
| y (series or vector, optional) |
If only the first two arguments are given, computes the correlogram for x for lags 1 to p. Let k represent the number of elements in x (1 if x is a series, the number of columns if x is a matrix, or the number of list-members if x is a list). The return value is a matrix with p rows and 2k columns, the first k columns holding the respective autocorrelations and the remainder the respective partial autocorrelations.
If a third argument is given, this function computes the cross-correlogram for each of the k elements in x and y, from lead p to lag p. The returned matrix has 2p + 1 rows and k columns. If x is series or list and y is a vector, the vector must have just as many rows as there are observations in the current sample range.
| Argument: | x (scalar, series or matrix) |
Returns the cosine of x. See also sin, tan, atan.
| Argument: | x (scalar, series or matrix) |
Returns the hyperbolic cosine of x.
| Arguments: | y1 (series or vector) |
| y2 (series or vector) |
Returns the covariance between y1 and y2. The arguments should be either two series, or two vectors of the same length. See also corr, mcov, mcorr.
| Arguments: | c (character) |
| ... (see below) | |
| p (scalar, series or matrix) |
Critical value calculator. Returns x such that P(X > x) = p, where the distribution X is determined by the character c. Between the arguments c and p, zero or more additional scalar arguments are required to specify the parameters of the distribution, as follows.
Standard normal (c = z, n, or N): no extra arguments
Student's t (t): degrees of freedom
Chi square (c, x, or X): degrees of freedom
Snedecor's F (f or F): df (num.); df (den.)
Binomial (b or B): probability; trials
Poisson (p or P): mean
Laplace (l or L): mean; scale
Standardized GED (E): shape
| Arguments: | A (matrix) |
| mode (scalar) |
Reinterprets a real matrix as holding complex values or vice versa. The precise action depends on mode (which must have value 1, 2, 3 or 4) as follows:
mode 1: A must be a real matrix with an even number of columns. Returns a complex matrix with half as many columns, the odd-numbered columns of A supplying the real parts and the even-numbered columns the imaginary parts.
mode 2: Performs the inverse operation of mode 1. A must be a complex matrix and the return value is a real matrix with twice as many columns as A.
mode 3: A must be a real matrix with an even number of rows. Returns a complex matrix with half as many rows, the odd-numbered rows of A supplying the real parts and the even-numbered rows the imaginary parts.
mode 4: Performs the inverse operation of mode 3. A must be a complex matrix and the return value is a real matrix with twice as many rows as A.
See also complex.
| Argument: | C (complex matrix) |
Returns an n x m complex matrix holding the conjugate transpose of the m x n complex matrix C. The ' (prime) operator also performs conjugate transposition for complex matrices. The transp function can be used on complex matrices but it performs "straight" transposition (not conjugated).
| Argument: | x (series or matrix) |
Cumulates x (that is, creates a running sum). When x is a series, produces a series y each of whose elements is the sum of the values of x to date; the starting point of the summation is the first non-missing observation in the currently selected sample. If any missing values are encountered in x, subsequent values of y will be set to missing. When x is a matrix, its elements are cumulated by columns.
In the case of panel data cumulation is in the time dimension, starting anew for each panel unit.
If you want cumulation to ignore missing values (that is, to treat them as if they were zeros), you can apply misszero to the argument, as in
series cx = cum(misszero(x))
See also diff.
| Argument: | &b (reference to bundle) |
Provides a somewhat flexible means of obtaining a text buffer containing data from an internet server, using libcurl. On input the bundle b must contain a string named URL which gives the full address of the resource on the target host. Other optional elements are as follows.
"header": a string specifying an HTTP header to be sent to the host.
"include": a scalar: if nonzero, the header received from the host is included with the output body.
"nobody": a scalar: if nonzero, the function will not download the body of the requested URL.
"postdata": a string holding data to be sent to the host.
The header and postdata fields are intended for use with an HTTP POST request; if postdata is present the POST method is implicit. Otherwise the GET or HEAD methods are implicit, depending on the value of the nobody key. (But note that for straightforward GET requests readfile offers a simpler interface.)
On completion of the request, the text received from the server is added to the bundle under the key "output", and the HTTP status code is stored under the key "http_code".
If an error occurs in formulating the request (for example there's no URL on input) the function fails, otherwise it returns 0 if the request succeeds or non-zero if it fails, in which case the error message from libcurl is added to the bundle under the key "errmsg". Note that "success" in this sense does not necessarily mean you got the data you wanted; all it means is that some response was received from the server. A quick way of checking is to inspect the HTTP status code: the most commonly used ones are 200 (success) or 404 (page not found). See https://en.wikipedia.org/wiki/List_of_HTTP_status_codes for the full list. Alternatively, you can check the content of the output buffer (which may in fact be a message such as "Page not found").
Here is an example of use: downloading some data from the US Bureau of Labor Statistics site, which requires sending a JSON query. Note the use of sprintf to embed double-quotes in the POST data.
bundle req
req.URL = "https://api.bls.gov/publicAPI/v1/timeseries/data/"
req.include = 1
eq.header = "Content-Type: application/json"
string s = sprintf("{\"seriesid\":[\"LEU0254555900\"]}")
req.postdata = s
err = curl(&req)
if err == 0
s = req.output
string line
loop while getline(s, &line)
printf "%s\n", line
endloop
endif
As a second example, the code below checks if a particular version of the "Global Macro Database" dataset is available, and downloads it only if so.
string base_URL = "https://www.globalmacrodata.com" string filename = "GMD_2025_03.csv" bundle req req.URL = base_URL ~ "/" ~ filename req.nobody = 1 err = curl(&req) if err || (req.http_code != 200) printf "Oh, oh. It seems %s is unavailable\n", filename else # actual request bundle req = empty req.URL = base_URL ~ "/" ~ filename err = curl(&req) print req endif
See also the functions jsonget and xmlget for means of processing JSON and XML data received, respectively.
| Arguments: | ed1 (integer) |
| ed2 (integer) | |
| weeklen (integer) |
Returns the number of (relevant) days between the epoch days ed1 and ed2, inclusive. The weeklen, which must equal 5, 6 or 7, gives the number of days in the week that should be counted (a value of 6 omits Sundays, and a value of 5 omits both Saturdays and Sundays).
To obtain epoch days from the more familiar form of dates, see epochday. Related: see smplspan.
| Argument: | x (matrix) |
This function returns the binary representation of the numbers contained in the column vector x, by storing each binary digit into a column of the returned matrix, which always has 32 columns. Each element of x must be an integer between 0 and 232-1. Otherwise, an error is flagged.
Note that the least significant bit comes in the first column. So column 1 corresponds to 20, column 2 to 21, and so on. For example, the expression
matrix B = dec2bin(5)
produces a row vector full of zeros except for positions 1 and 3.
The bin2dec function performs the inverse transformation.
| Argument: | ... (see below) |
Enables the definition of an array variable in extenso, by providing one or more elements. In using this function you must specify a type (in plural form) for the array: strings, matrices, bundles or lists. Each of the arguments must evaluate to an object of the specified type. On successful completion, the return value is an array of n elements, where n is the number of arguments.
strings S = defarray("foo", "bar", "baz")
matrices M = defarray(I(3), X'X, A*B, P[1:])
See also array.
| Argument: | ... (see below) |
Enables the initialization of a bundle variable in extenso, by providing zero or more pairs of the form key, member. If we count the arguments from 1, every odd-numbered argument must evaluate to a string (key) and every even-numbered argument must evaluate to an object of a type that can be included in a bundle.
A couple of simple examples:
bundle b1 = defbundle("s", "Sample string", "m", I(3))
bundle b2 = defbundle("yn", normal(), "x", 5)
The first example creates a bundle with members a string and a matrix; the second, a bundle with a series member and a scalar member. Note that you cannot specify a type for each argument when using this function, so you must accept the "natural" type of the argument in question. If you wanted to add a series with constant value 5 to a bundle named b1 it would be necessary to do something like the following (after declaring b1):
series b1.s5 = 5
If no arguments are given to this function it is equivalent to creating an empty bundle (or to emptying an existing bundle of its content), as could also be done via
bundle b = null
Two alternative forms of syntax are available for defining bundles. In each case the keyword defbundle is replaced by a single underscore. In the first variant the comma-separated arguments take the form key=value, where the key is taken to be a literal string and does not require quotation. Here is an example:
bundle b = _(x=5, strval="some string", m=I(3))
This form is particularly convenient for constructing an anonymous bundle on the fly as a function argument, as in
b = regls(ys, LX, _(lfrac=0.35, stdize=0))
where the regls function takes an optional bundle argument holding various parameters.
The second variant is designed for the case where you wish to pack several pre-existing named objects into a bundle: you just give their names, unquoted:
bundle b = _(x, y, z)
Here the object x is copied into the bundle under the key "x", and similarly for y and z.
These alternative forms involve less typing than the full defbundle() version and are likely to be more convenient in many cases, but note that they are less flexible. Only the full version can handle keys given as string variables rather than literal strings.
| Argument: | ... (see below) |
Defines a list (of named series), given one or more suitable arguments. Each argument must be a named series (given by name or integer ID number), an existing named list, or an expression which evaluates to a list (including a vector which can be interpreted as a set of series ID numbers).
One point to note: this function simply concatenates its arguments to produce the list that it returns. If the intent is that the return value does not contain duplicates (does not reference any given series more than once), it is up to the caller to ensure that requirement is satisfied.
| Arguments: | x (series) |
| opts (bundle, optional) |
The primary purpose of this function is to produce a deseasonalized version of the (quarterly or monthly) input series x, using X-13ARIMA-SEATS; it is available only if X-13ARIMA-SEATS is installed. If the second, optional argument is omitted, seasonal adjustment is carried out with all X-13ARIMA options at their default values (fully automatic procedure). When opts is supplied, it may contain any of the following option specifications.
verbose: what to print? 0 = nothing (the default); 1 = confirmation of the options selected; 2 = confirmation of options plus the output from X-13ARIMA.
seats: 1 to use the SEATS algorithm in place of the default X11 algorithm for seasonal adjustment, or 0.
airline: 1 to use the "airline" ARIMA model specification (0,1,1)(0,1,1) in place of the default automatic model selection, or 0.
arima: can be used to impose a chosen ARIMA specification, in the form of a 6-vector holding small non-negative integers. These are given the (p,d,q,P,D,Q) interpretation, in traditional time-series notation: the first three terms represent the non-seasonal AR, Integration and MA orders, and the last three the seasonal counterparts. If both airline and arima are given, arima takes precedence.
outliers: enable detection and correction for outliers (choices 1 through 7), or 0 (the default) to omit this feature. The three available outlier types with their numerical codes are: 1 = additive outlier (ao), 2 = level shift (ls), 4 = temporary change (tc). To combine options you add the codes, for example 1 + 2 + 4 = 7 to activate all three. Note that the choice 3 = 1 + 2 (ao and ls) is the default within X-13ARIMA-SEATS, and is selected via the outlier tickbox in gretl's dialog window for seasonal adjustment via X13.
critical: a positive scalar, the critical value for defining outliers, the default being automatic, dependent on the sample size. Relevant only when outliers is specified.
logtrans: should the input series be put in log form? 0 = no, 1 = yes, 2 = automatically selected (the default). Note that it is not recommended to pass the input series in log form; if you want the log to be used, pass the "raw" level but specify logtrans=1.
trading_days: should trading-day effects be included? 0 = no, 1 = yes, 2 = automatic (the default).
working_days: a simpler version of trading_days with a single distinction between weekdays and weekends rather than individual day effects. 0 = no (the default), 1 = yes, 2 = automatic. Use only one of trading_days and working_days.
easter: 1 to allow for an easter effect, as a supplement to either trading_days or working_days, or 0 (the default).
output: a string to select the type of the output series, "sa" for deseasonalized (the default), "trend" for the estimated trend, or "irreg" for the irregular component.
save_spc: boolean flag, default 0; see below.
In some cases one may wish to obtain all three of the results available from X-13ARIMA via a single call to deseas. This is supported as follows. Pass the opts bundle in pointer form, and give the string "all" under the output key. The direct return value is then the seasonally adjusted series, but on successful completion opts will contain a matrix named results with three columns: seasonally adjusted, trend and irregular. Here's an illustration (where the direct return value is discarded).
bundle b = _(output="all") deseas(y, &b) series y_dseas = b.results[,1] series y_trend = b.results[,2] series y_irreg = b.results[,3]
The save_spc flag can be used to save the content of the X-13ARIMA input file written by gretl. The options bundle should be passed in pointer form and the specification (as a string) can be found under the key x13a_spc. The following code illustrates saving this to file under the name myspec.spc in the user's working directory. (Note that the .spc extension is required by X-13ARIMA.)
bundle b = _(save_spc=1) deseas(y, &b) outfile myspec.spc print b.x13a_spc end outfile
| Argument: | A (square matrix) |
Returns the determinant of A, computed via the LU factorization. If what you actually want is the log determinant you should call ldet instead. See also rcond, cnumber.
| Argument: | X (matrix) |
Returns the principal diagonal of X in a column vector. Note: if X is an m x n matrix, the number of elements of the output vector is min(m, n). See also tr.
| Arguments: | A (matrix) |
| B (matrix) |
Returns the direct sum of A and B, that is a matrix holding A in its north-west corner and B in its south-east corner. If both A and B are square, the resulting matrix is block-diagonal.
| Argument: | y (series, matrix or list) |
Computes first differences. If y is a series, or a list of series, starting values are set to NA. If y is a matrix, differencing is done by columns and starting values are set to 0.
When a list is returned, the individual variables are automatically named according to the template d_ varname where varname is the name of the original series. The name is truncated if necessary, and may be adjusted in case of non-uniqueness in the set of names thus constructed.
| Argument: | x (scalar, series or matrix) |
Returns the digamma (or Psi) function of x, that is the derivative of the log of the Gamma function.
| Arguments: | X (matrix) |
| metric (string, optional) | |
| Y (matrix, optional) |
Computes distances between points on a metric that can be euclidean (the default), manhattan, hamming, chebyshev, cosine or mahalanobis. The string identifying the metric can be given as an unambiguous truncation. The additional metrics correlation and standardized Euclidean are supported via simple transformations of the inputs; see below.
Each row of the m x n matrix X is treated as a point in an n-dimensional space; in an econometric context this is likely to represent a single observation comprising the values of n variables.
If the optional argument Y is not given, the return value is a column vector of length m(m – 1)/2 comprising the non-redundant subset of all pairwise distances between the m points (rows of X). Given such a vector named d, the full symmetric matrix of inter-point distances (with zeros on the principal diagonal) can be constructed via
D = unvech(d, 0)
since d is akin to the vech of D, with diagonal elements omitted. The optional second argument to unvech says that the diagonal should be filled with zeros.
If Y is given, it must be a p x n matrix, each row of which is again treated as a point in n-space. In this case the return value is an m x p matrix whose i,j element holds the distance between row i of X and row j of Y.
To obtain the distances from a given reference point to each of n data-points, give Y as a single row. If the reference point is the centroid in the usual sense (vector of sample means), give meanc(X) as the Y value.
euclidean: the square root of the sum of squared deviations in each of the dimensions.
manhattan: the sum of the absolute deviations in each of the dimensions.
hamming: the proportion of the dimensions in which the deviation is non-zero (so bounded by 0 and 1).
chebyshev: the greatest absolute deviation in any dimension.
cosine: 1 minus the cosine of the angle between the "points", considered as vectors.
Mahalanobis: works like euclidean except that the distances are scaled by the inverse of a covariance matrix, giving the n-dimensional counterpart of a z-score. See also Mahalanobis notes below, and https://en.wikipedia.org/wiki/Mahalanobis_distance for further elucidation.
In the most common usage of Mahalanobis distances the centroid is the vector of sample means and scaling is by the inverse covariance of the columns of X. Specifically this means that X (and also Y, if present) is multiplied by an upper triangular matrix, the transpose of the inverse cholesky factor of the covariance matrix. To obtain this result you can do
dmahal = distance(X, "mahal", meanc(X))
For a series or list argument, the mahal command produces the same result.
To obtain the Mahalanobis distances of the rows of X from an arbitrary centroid, c, using an arbitrary covariance matrix, V, the following method can be used.
U = cholesky(V)' d = distance(X / U, "euc", c / U)
Standardized Euclidean distances and correlation distances can be obtained as follows:
# standardized euclidean dseu = distance(stdize(X), "euc") # correlation (based on cosine) dcor = distance(stdize(X', -1)', "cos")
| Argument: | x (scalar, series or matrix) |
Returns the density of the standard normal distribution at x. To get the density for a non-standard normal distribution at x, pass the z-score of x to the dnorm function and multiply the result by the Jacobian of the z transformation, namely 1 over σ, as illustrated below:
mu = 100 sigma = 5 x = 109 fx = (1/sigma) * dnorm((x-mu)/sigma)
| Arguments: | X (list) |
| epsilon (scalar, optional) |
Returns a list with the same elements as X, but for the collinear series. Therefore, if all the series in X are linearly independent, the output list is just a copy of X.
The algorithm uses the QR decomposition (Householder transformation), so it is subject to finite precision error. In order to gauge the sensitivity of the algorithm, a second optional parameter epsilon may be specified to make the collinearity test more or less strict, as desired. The default value for epsilon is 1.0e-8. Setting epsilon to a larger value increases the probability of a series to be dropped.
Example:
nulldata 20 set seed 9876 series foo = normal() series bar = normal() series foobar = foo + bar list X = foo bar foobar list Y = dropcoll(X) list print X list print Y # set epsilon to a ridiculously small value list Y = dropcoll(X, 1.0e-30) list print Y
produces
? list print X foo bar foobar ? list print Y foo bar ? list Y = dropcoll(X, 1.0e-30) Replaced list Y ? list print Y foo bar foobar
| Argument: | x (series, vector or strings array) |
Sorts x in descending order, skipping observations with missing values when x is a series. See also sort, values.
| Arguments: | x (series) |
| omitval (scalar, optional) |
The argument x should be a discrete series. This function creates a set of dummy variables coding for the distinct values in the series. By default the smallest value is taken as the omitted category and is not explicitly represented.
The optional second argument represents the value of x which should be treated as the omitted category. The effect when a single argument is given is equivalent to dummify(x, min(x)). To produce a full set of dummies, with no omitted category, use dummify(x, NA).
The generated variables are automatically named according to the template Dvarname_i where varname is the name of the original series and i is a 1-based index. The original portion of the name is truncated if necessary, and may be adjusted in case of non-uniqueness in the set of names thus constructed.
| Argument: | y (scalar, series or matrix) |
Given the year in argument y, returns the date of Easter on the Gregorian calendar as month + day/100. For example, in 2014 the date of Easter was April 20, which is represented under this convention as 4.2. (Note that April 2 would be returned as 4.02.) The following code shows how month and day can be extracted from the return value.
scalar e = easterday(2014) scalar m = floor(e) scalar d = round(100*(e-m))
| Argument: | y (series or vector) |
Calculates the empirical CDF of y. This is returned in a matrix with two columns: the first holds the sorted unique values of y and the second holds the cumulative relative frequency, that is the count of observations whose value is less than or equal to the value in the first column, divided by the total number of observations.
| Arguments: | A (square matrix) |
| &V (reference to matrix, or null) | |
| &W (reference to matrix, or null) |
Computes the eigenvalues, and optionally the right and/or left eigenvectors, of the n x n matrix A, which may be real or complex. The eigenvalues are returned in a complex column vector. To obtain the norm of the eigenvalues, you can use the abs function, which accepts complex arguments.
If you wish to retrieve the right eigenvectors (as an n x n complex matrix), supply the name of an existing matrix, preceded by & to indicate the "address" of the matrix in question, as the second argument. Otherwise this argument can be omitted.
To retrieve the left eigenvectors (again, as a complex matrix), supply a matrix-address as the third argument. Note that if you want the left eigenvectors but not the right ones, you should use the keyword null as a placeholder for the second argument.
See also eigensym, eigsolve, svd.
| Arguments: | A (symmetric matrix) |
| &U (reference to matrix, or null) |
Works mostly as eigen except that the argument A must be symmetric (in which case less calculation is required), and the eigenvalues are returned in ascending order. If you want to get the eigenvalues in descending order (and have the eigenvectors reordered correspondingly) you can do the following:
matrix U e = eigensym(A, &U) Tmp = msortby((-e' | U)',1)' e = -Tmp[1,]' U = Tmp[2:,] # now largest to smallest eigenvalues print e U
Note: if you're interested in the eigen-decomposition of a matrix of the form X'X it's preferable to compute the argument via the prime operator X'X rather than using the more general syntax X'*X. The former expression uses a specialized algorithm which offers greater computational efficiency as well as ensuring that the result is exactly symmetric.
| Arguments: | A (symmetric matrix) |
| B (symmetric matrix) | |
| &U (reference to matrix, or null) |
Solves the generalized eigenvalue problem |A – λB| = 0, where both A and B are symmetric and B is positive definite. The eigenvalues are returned directly, arranged in ascending order. If the optional third argument is given it should be the name of an existing matrix preceded by &; in that case the generalized eigenvectors are written to the named matrix.
| Arguments: | year (scalar or series) |
| month (scalar or series) | |
| day (scalar or series) |
Returns the number of the day in the current epoch specified by year, month and day. The epoch day equals 1 for the first of January in the year 1 AD on the proleptic Gregorian calendar; it stood at 733786 on 2010-01-01. If any of the arguments are given as series the value returned is a series, otherwise it is a scalar.
By default the year, month and day values are assumed to be given relative to the Gregorian calendar, but if the year is a negative value the interpretation switches to the Julian calendar.
An alternative call is also supported: if a single argument is given, it is taken to be a date (or series of dates) in ISO 8601 "basic" numeric format, YYYYMMDD. So the following two calls produce the same result, namely 700115.
eval epochday(1917, 11, 7) eval epochday(19171107)
For the inverse function, see isodate and also (for the Julian calendar) juldate. For another means of converting dates to epoch days see strpday.
| Argument: | errno (integer) |
Retrieves the gretl error message associated with errno. See also $error.
| Arguments: | condition (boolean) |
| msg (string) |
Applicable only in the context of a user-defined function, or within an mpi block. If condition evaluates as non-zero, it causes execution of the current function to terminate with an error condition flagged; the msg argument is then printed as part of the message shown to the caller of the function in question.
The return value from this function (1) is purely nominal.
| Argument: | name (string) |
Returns non-zero if name, which should be valid as a gretl identifier, names a currently defined object, be it a scalar, a series, a matrix, list, string, bundle or array; otherwise returns 0.
Intended usage is for the case where a user-defined function has an optional parameter with a null default. The function writer can use exists(), passing the parameter name, to check whether or not the caller supplied an argument. But please note, lists are an exception in this respect: if a list parameter has a null default and the caller doesn't supply an argument, the function gets an empty list rather than no list; therefore exists will always return non-zero. To check for emptiness of a list argument, use nelem.
For related checks, see typeof and inbundle.
| Argument: | x (scalar, series or matrix) |
Returns ex. Note that in case of matrix input the function acts element by element. For the matrix exponential function, see mexp.
| Arguments: | y (series or vector) |
| f (series, list or matrix) | |
| U2 (boolean, optional) |
Produces a matrix holding several statistics which serve to evaluate f as a forecast of the observed data y.
If f is a series or vector the output is a column vector; if f is a list with k members or a T x k matrix the output has k columns, each of which holds statistics for the corresponding element (series or column) of the input as a forecast of y.
In all cases the "vertical" dimension of the input (for a series or list the length of the current sample range, for a matrix the number of rows) must match across the two arguments.
The rows of the returned matrix are as follows:
1 Mean Error (ME) 2 Root Mean Squared Error (RMSE) 3 Mean Absolute Error (MAE) 4 Mean Percentage Error (MPE) 5 Mean Absolute Percentage Error (MAPE) 6 Theil's U (U1 or U2) 7 Bias proportion, UM 8 Regression proportion, UR 9 Disturbance proportion, UD
The variant of Theil's U shown by default depends on the nature of the data: if they are known to be time series then U2 is shown, otherwise U1 is produced. But this choice can be forced via the optional trailing argument: give a non-zero value to force U2, or zero to force U1.
For details on the calculation of these statistics, and the interpretation of the U values, please see chapter 35 of the Gretl User's Guide.
| Arguments: | b (column vector) |
| fcall (function call) | |
| h (scalar, optional) |
Calculates a numerical approximation to the Jacobian associated with the n-vector b and the transformation function specified by the argument fcall. The function call should take b as its first argument (either straight or in pointer form), followed by any additional arguments that may be needed, and it should return an m x 1 matrix. On successful completion fdjac returns an m x n matrix holding the Jacobian.
The optional third argument can be used to set the step size h used in the approximation mechanism (see below); if this argument is omitted the step size is determined automatically.
Here is an example of usage:
matrix J = fdjac(theta, myfunc(&theta, X))
The function can use three different methods: simple forward-difference, bilateral difference or 4-nodes Richardson extrapolation. Respectively:
J0 = (f(x+h) - f(x))/h
J1 = (f(x+h) - f(x-h))/2h
J2 = [8(f(x+h) - f(x-h)) - (f(x+2h) - f(x-2h))] /12h
The three alternatives above provide, generally, a trade-off between accuracy and speed. You can choose among methods via the set command: specify a value of 0, 1 or 2 for the fdjac_quality variable. The default is 0.
For more details and examples chapter 37 of the Gretl User's Guide.
See also BFGSmax, numhess, set.
| Arguments: | funcname (string) |
| ... (see below) |
Primarily useful for writers of functions. The first argument should be the name of a function; the remaining arguments will be passed to the specified function. This permits treating the function identified by funcname as itself a variable. The return value is whatever the named function returns given the specified arguments.
The example below illustrates some possible uses.
function scalar utility (scalar c, scalar sigma)
return (c^(1-sigma)-1)/(1-sigma)
end function
strings S = defarray("log", "utility")
# call a 1-argument built-in function
x = feval(S[1], 2.5)
# call a user-defined function
x = feval(S[2], 5, 0.5)
# a 2-argument built-in function
func = "zeros"
m = feval(func, 5-2, sqrt(4))
print m
# a 3-argument built-in
x = feval("monthlen", 12, 1980, 5)
There's a weak analogy between feval and genseries: both functions render variable a syntactic element that is usually fixed at the time a script is composed.
See also fevalb.
| Arguments: | funcname (string) |
| b (bundle) |
This is a variant of feval which meets a case that may be encountered by function writers, where the number and types of the arguments to be passed to the named function are not known in advance. Instead of the arguments being passed individually, they are passed as members of the bundle argument b.
Since the order of the members in a gretl bundle is indeterminate, some mechanism is required to ensure that they are passed to the function in question in the right order. This is automatically ensured if the lexicographic order of the keys in the bundle gives the argument order. For examples, the keys could be arg1, arg2 and so on (or arg01, arg02 and so on in the unlikely event that the function takes more than nine arguments). Alternatively, the bundle may contain an array of strings under the reserved key arglist. This array must hold exactly the keys in b, except for arglist itself, in the desired order.
The examples below illustrate both approaches, as applied to the monthlen function.
# using lexicographic order
bundle b = _(arg1=12, arg2=1980, arg3=5)
n = feval("monthlen", b)
# using arglist
bundle b = _(month=12, year=1980, wkdays=5)
b.arglist = defarray("month", "year", "wkdays")
n = feval("monthlen", b)
See also feval.
| Arguments: | target (integer) |
| shock (integer) | |
| sys (bundle, optional) |
This function provides a more flexible alternative to the accessor $fevd for obtaining a forecast error variance decomposition (FEVD) matrix following estimation of a VAR or VECM. Without the final optional argument, it is available only when the last model estimated was a VAR or VECM. Alternatively, information on such a system can be stored in a bundle via the $system accessor and subsequently passed to fevd.
The target and shock arguments take the form of 1-based indices of the endogenous variables in the system, with 0 taken to mean "all". The following code fragment illustrates usage. In the first example the matrix fe1 holds the shares of the FEVD for y1 due to each of y1, y2 and y3 (the rows therefore summing to 1). In the second, fe2 holds the contribution of y2 to the forecast error variance of all three variables (so the rows do not sum to 1). In the third case the return value is a column vector showing the "own share" of the FEVD for y1.
var 4 y1 y2 y3 bundle vb = $system matrix fe1 = fevd(1, 0, vb) matrix fe2 = fevd(0, 2, vb) matrix fe3 = fevd(1, 1, vb)
The number of periods (rows) over which the decomposition is traced is determined automatically based on the frequency of the data, but this can be overridden via the horizon argument to the set command, as in set horizon 10.
See also irf.
| Argument: | X (matrix) |
Discrete Fourier transform. The input matrix X may be real or complex. The output is a complex matrix of the same dimensions as X.
Should it be necessary to compute the Fourier transform on several vectors with the same number of elements, it is more efficient to group them into a matrix rather than invoking fft for each vector separately. See also ffti.
| Argument: | X (matrix) |
Inverse discrete Fourier transform. It is assumed that X contains n complex column vectors. A matrix with n columns is returned.
Should it be necessary to compute the inverse Fourier transform on several vectors with the same number of elements, it is more efficient to group them into a matrix rather than invoking ffti for each vector separately. See also fft.
| Arguments: | x (series or matrix) |
| a (scalar or vector, optional) | |
| b (scalar or vector, optional) | |
| y0 (scalar, optional) | |
| x0 (scalar or vector, optional) |
Computes an ARMA-like filtering of the argument x. The transformation can be written as
yt = a0 xt + a1 xt-1 + ... aq xt-q + b1 yt-1 + ... bpyt-p
If argument x is a series, the result will be itself a series. Otherwise, if x is a matrix with T rows and k columns, the result will be a matrix of the same size, in which the filtering is performed column by column.
The two arguments a and b are optional. They may be scalars, vectors or the keyword null.
If a is a scalar, this is used as a0 and implies q=0; if it is a vector of q+1 elements, they contain the coefficients from a0 to aq. If a is null or omitted, this is equivalent to setting a0 =1 and q=0.
If b is a scalar, this is used as b1 and implies p=1; if it is a vector of p elements, they contain the coefficients from b1 to bp. If b is null or omitted, this is equivalent to setting B(L)=1.
The optional scalar argument y0 is taken to represent all values of y prior to the beginning of sample (used only when p > 0). If omitted, it is understood to be 0. Similarly, the optional argument x0 may be used to specify one or more pre-sample values of x, information that is relevant only when q > 0. Otherwise pre-sample values of x are assumed to be zero.
See also bkfilt, bwfilt, fracdiff, hpfilt, movavg, varsimul.
Example:
nulldata 5 y = filter(index, 0.5, -0.9, 1) print index y --byobs x = seq(1,5)' ~ (1 | zeros(4,1)) w = filter(x, 0.5, -0.9, 1) print x w
produces
index y
1 1 -0.40000
2 2 1.36000
3 3 0.27600
4 4 1.75160
5 5 0.92356
x (5 x 2)
1 1
2 0
3 0
4 0
5 0
w (5 x 2)
-0.40000 -0.40000
1.3600 0.36000
0.27600 -0.32400
1.7516 0.29160
0.92356 -0.26244
| Arguments: | y (series) |
| insample (boolean, optional) |
Returns the 1-based index of the first non-missing observation for the series y. By default the whole data range is examined, so if subsampling is in effect the value returned may be smaller than the accessor $t1. But if a non-zero value is given for insample only the current sample range is considered. See also lastobs.
| Arguments: | rawname (string) |
| underscore (boolean, optional) |
Primarily intended for use in connection with the join command. Returns the result of converting rawname to a valid gretl identifier, which must start with a letter, contain nothing but (ASCII) letters, digits and the underscore character, and must not exceed 31 characters. The rules used in conversion are:
1. Skip any leading non-letters.
2. Until the 31-character limit is reached or the input is exhausted: transcribe "legal" characters; skip "illegal" characters apart from spaces; and replace one or more consecutive spaces with an underscore, unless the previous character transcribed is an underscore in which case space is skipped.
If you are confident that the input is not too long (and hence subject to truncation), you may wish to have sequences of one or more illegal characters replaced with an underscore rather than just being deleted; this may produce a more readable identifier. To get this effect, supply a nonzero value for the optional second argument. But this is not advisable in the context of the join command, since the automatically "fixed" name will not use underscores in this way.
| Arguments: | A (array of matrices or strings) |
| alt (integer or string, optional) |
"Flattens" either an array of matrices into a single matrix or an array of strings into a single string.
In the matrix case, the way the matrices in A are joined together depends on the the alt argument, which should have value 0 (horizontal), 1 (vertical) or 2 ("vec-wise"). The best way to explain the difference between the three alternatives is by example: the code
X = {1,3,5; 2,4,6}
A = defarray(X, X+6)
U = flatten(A,0) # = A[1] ~ A[2]
V = flatten(A,1) # = A[1] | A[2]
W = flatten(A,2) # = vec(A[1]) ~ vec(A[2])
produces the following three matrices:
U (2 x 6) 1 3 5 7 9 11 2 4 6 8 10 12 V (4 x 3) 1 3 5 2 4 6 7 9 11 8 10 12 W (6 x 2) 1 7 2 8 3 9 4 10 5 11 6 12
An error is flagged if the matrices in the array are not conformable for the operation. See msplitby for the inverse operation.
In the string case the result holds the strings in A, arranged one per line by default. If a non-zero numerical value is given for alt the strings are separated by spaces rather than newlines, but an alternative usage of alt is supported: you may give a specific string to use as the separator. The inverse function for the string case is strsplit.
| Argument: | y (scalar, series or matrix) |
Returns the greatest integer less than or equal to x. Note: int and floor differ in their effect for negative arguments: int(-3.5) gives –3, while floor(-3.5) gives –4.
| Arguments: | y (series) |
| d (scalar) |
Returns the fractional difference of order d for the series y.
Note that in theory fractional differentiation is an infinitely long filter. In practice, presample values of yt are assumed to be zero.
A negative value of d can be given, in which case fractional integration is performed.
| Arguments: | fcall (function call) |
| init (scalar or vector, optional) | |
| toler (scalar, optional) |
Attempts to find a single root of a continuous (typically nonlinear) function f—that is, a value of the scalar variable x such that f(x) = 0. The fcall argument should provide a call to the function in question; fcall may include an arbitrary number of arguments but the first one must be the scalar playing the role of x. On successful completion the value of the root is returned.
The method used is that of Ridders (1979). This requires an initial bracket {x0, x1} such that both x values lie in the domain of the function and the respective function values are of opposite sign. Best results are likely to be obtained if the user can supply, via the second argument, a 2-vector holding suitable end-points for the bracket. Failing that, one can supply a single scalar value and fzero will try to find a counterpart. If the second argument is omitted, x0 is initialized to a small positive value and we search for a suitable x1.
The optional toler argument can be used to adjust the maximum acceptable absolute difference of f(x) from zero, the default being 1.0e–14.
By default this function operates silently, but the progress of the iterative method can be exposed by executing the command "set max_verbose on" before calling fzero.
Some simple examples follow.
# Approximate pi by finding a zero for sin() in the
# bracket 2.8 to 3.2
x = fzero(sin(x), {2.8, 3.2})
printf "\nx = %.12f vs pi = %.12f\n\n", x, $pi
# Approximate the 'Omega constant' starting from x = 0.5
function scalar f(scalar x)
return log(x) + x
end function
x = fzero(f(x), 0.5)
printf "x = %.12f f(x) = %.15f\n", x, f(x)
| Argument: | x (scalar, series or matrix) |
Returns the gamma function of x.
See also bincoeff and lngamma.
| Arguments: | varname (string) |
| rhs (series) |
Provides the script writer with a convenient means of generating series whose names are not known in advance, and/or creating a series and appending it to a list in a single operation.
The first argument gives the name of the series to create (or modify); this can be a string literal, a string variable, or an expression that evaluates to a string. The second argument, rhs ("right-hand side"), defines the source series: this can be the name of an existing series or an expression that evaluates to a series, as would appear to the right of the equals sign when defining a series in the usual way.
The return value from this function is the ID number of the series in the dataset, a value suitable for inclusion in a list (or –1 on failure).
For example, suppose you want to add n random normal series to the dataset and put them all into a named list. The following will do the job:
nulldata 10
list Normals = null
scalar n = 3
loop i = 1 .. n
Normals += genseries(sprintf("norm%d", i), normal())
endloop
On completion Normals will contain the series norm1, norm2 and norm3 .
Those who find genseries useful may also like to explore feval.
| Arguments: | mapfile (string) |
| payload (series, optional) | |
| options (bundle, optional) |
Calls for production of a map, when suitable geographical data are present. In most cases the mapfile argument should be given as $mapfile, an accessor that retrieves the name of the relevant GeoJSON file or ESRI shapefile. The optional payload argument is used to give the name of a series with which to colorize the regions of the map. And the final bundle argument enables you to set numerous options.
See the geoplot documentation, geoplot.pdf, for full details and examples. This explains all the settings configurable via the options argument.
| Argument: | s (string) |
If an environment variable by the name of s is defined, returns the string value of that variable, otherwise returns an empty string. See also ngetenv.
| Argument: | y (series) |
Returns information on the specified series, which may be given by name or ID number. The returned bundle contains all the attributes which can be set via the setinfo command. It also contains additional information relevant for series that have been created as transformations of primary data (lags, logs, etc.): this includes the gretl command word for the transformation under the key "transform" and the name of the associated primary series under "parent". For lagged series, the specific lag number can be found under the key "lag".
Here is an example of usage:
open data9-7 lags QNC bundle b = getinfo(QNC_2) print b
On executing the above we see:
has_string_table = 0 lag = 2 parent = QNC name = QNC_2 graph_name = coded = 0 discrete = 0 transform = lags description = = QNC(t - 2)
To test whether series 5 in a dataset is a lagged term one can do this sort of thing:
if getinfo(5).lag != 0 printf "series 5 is a lag of %s\n", getinfo(5).parent endif
Note that the dot notation to access bundle members can be used even when the bundle is "anonymous" (not saved under its own name).
| Argument: | b (bundle) |
Returns an array of strings holding the keys identifying the contents of b. If the bundle is empty an empty array is returned.
| Arguments: | source (string) |
| &target (reference to string) |
This function is used to read successive lines from source, which should be a named string variable. On each call a line from the source is written to target (which must also be a named string variable, given in pointer form), with the newline character stripped off. The valued returned is 1 if there was anything to be read (including blank lines), 0 if the source has been exhausted.
Here is an example in which the content of a text file is broken into lines:
string s = readfile("data.txt")
string line
scalar i = 1
loop while getline(s, &line)
printf "line %d = '%s'\n", i++, line
endloop
In this example we can be sure that the source is exhausted when the loop terminates. If the source might not be exhausted you should follow your regular call(s) to getline with a "clean up" call, in which target is replaced by null (or omitted altogether) as in
getline(s, &line) # get a single line getline(s, null) # clean up
Note that although the reading position advances at each call to getline, source is not modified by this function, only target.
| Arguments: | C (matrix) |
| A (matrix) | |
| B (matrix) | |
| U (matrix) | |
| &dP (reference to matrix, or null) |
Computes the GHK (Geweke, Hajivassiliou, Keane) approximation to the multivariate normal distribution function; see for example Geweke (1991). The value returned is an n x 1 vector of probabilities.
The argument C (m x m) should give the Cholesky factor (lower triangular) of the covariance matrix of m normal variates. The arguments A and B should both be n x m, giving respectively the lower and upper bounds applying to the variates at each of n observations. Where variates are unbounded, this should be indicated using the built-in constant $huge or its negative.
The matrix U should be m x r, with r the number of pseudo-random draws from the uniform distribution; suitable functions for creating U are muniform and halton.
We illustrate below with a relatively simple case where the multivariate probabilities can be calculated analytically. The series P and Q should be numerically very similar to one another, P being the "true" probability and Q its GHK approximation:
nulldata 20
series inf1 = -2*uniform()
series sup1 = 2*uniform()
series inf2 = -2*uniform()
series sup2 = 2*uniform()
scalar rho = 0.25
matrix V = {1, rho; rho, 1}
series P = cdf(D, rho, inf1, inf2) - cdf(D, rho, sup1, inf2) \
- cdf(D, rho, inf1, sup2) + cdf(D, rho, sup1, sup2)
C = cholesky(V)
U = halton(2, 100)
series Q = ghk(C, {inf1, inf2}, {sup1, sup2}, U)
The optional dP argument can be used to retrieve the n x k matrix of analytical derivatives of the probabilities, where k equals 2m + m(m + 1)/2. The first m columns hold the derivatives with respect to the lower bounds, the next m those with respect to the upper bounds, and the remainder the derivatives with respect to the unique elements of the C matrix in "vech" order.
| Argument: | y (series or vector) |
Returns Gini's inequality index for the (non-negative) series or vector y. A Gini value of zero indicates perfect equality. The maximum Gini value for a series with n members is (n – 1)/n, occurring when only one member has a positive value; a Gini of 1.0 is therefore the limit approached by a large series with maximal inequality.
| Arguments: | A (matrix) |
| tol (scalar, optional) |
Returns A+, the Moore–Penrose or generalized inverse of the r x c matrix A, computed via the singular value decomposition.
The result of this operation depends on the number of singular values of A that are found to be numerically 0. The tol optional parameter can be used for tweaking this aspect. Singular values are considered to be 0 if they are less than m × tol × s, where m is the greater of r and c and s is the largest singular value. If the second argument is omitted tol is set to machine epsilon (see $macheps). In some cases, you may want to set tol to a larger value (eg 1.0e-9) in order to avoid overestimating the rank of A, which may lead to numerically unstable results.
This matrix has the properties A A+ A = A and A+ A A+ = A+. Moreover, the products A A+ and A+ A are symmetric by construction.
| Arguments: | &b (reference to matrix) |
| f (function call) | |
| toler (scalar, optional) |
One-dimensional maximization via the Golden Section Search method. The matrix b should be a 3-vector. On input the first element is ignored while the second and third elements set the lower and upper bounds on the search. The fncall argument should specify a call to a function that returns the value of the maximand; element 1 of b, which will hold the current value of the adjustable parameter when the function is called, should be given as its first argument; any other required arguments may then follow. The function in question should be unimodal (should have no local maxima other than the global maximum) over the stipulated range, or GSS is not sure to find the maximum.
On successful completion GSSmax returns the optimum value of the maximand, while b holds the optimal parameter value along with the limits of its bracket.
The optional third argument may be used to set the tolerance for convergence, that is, the maximum acceptable width of the final bracket for the parameter. If this argument is not given a value of 0.0001 is used.
If the object is in fact minimization, either the function call should return the negative of the criterion or alternatively GSSmax may be called under the alias GSSmin.
Here is a simple example of usage:
function scalar trigfunc (scalar theta)
return 4 * sin(theta) * (1 + cos(theta))
end function
matrix m = {0, 0, $pi/2}
eval GSSmax(&m, trigfunc(m[1]))
printf "\n%10.7f", m
An alias for GSSmax; if called under this name the function acts as a minimizer.
| Arguments: | m (integer) |
| r (integer) | |
| offset (integer, optional) |
Returns an m x r matrix containing m Halton sequences of length r. The sequences are constructed using the first m primes. By default the first 10 elements of each sequence are discarded, but this figure can be adjusted via the optional offset argument, which should be a non-negative integer. See Halton and Smith (1964).
| Arguments: | X (matrix) |
| Y (matrix, optional) |
Horizontal direct product. The two arguments must have the same number of rows, r. The return value is a matrix with r rows, in which the i-th row is the Kronecker product of the corresponding rows of X and Y. If Y is omitted, the "shorthand" syntax applies (see below).
If X is an r x k matrix and Y is an r x m matrix, the result will be a matrix with r rows and km columns.
This operation is called "horizontal direct product" in conformity to its implementation in the GAUSS programming language. Its equivalent in standard matrix algebra would be called the row-wise Khatri-Rao product, or "face-splitting" product in the signal processing literature.
Example: the code
A = {1,2,3; 4,5,6}
B = {0,1; -1,1}
C = hdprod(A, B)
produces the following matrix:
0 1 0 2 0 3
-4 4 -5 5 -6 6
If X and Y are the same matrix, then each row of the result is the vectorization of a symmetric matrix. In these cases, the second argument may be omitted; however, the returned matrix will only contain the non-redundant columns, and will therefore have k(k+1)/2 columns. For example,
A = {1,2,3; 4,5,6}
C = hdprod(A)
produces
1 2 3 4 6 9 16 20 24 25 30 36
Note that the i-th row of C is vech(ai ai'), where ai is the i-th row of A.
When using the shorthand syntax with complex matrices, the implicit second argument will be the conjugate of the first one, so as to make each row of the result the symmetric vectorization of a Hermitian matrix.
| Arguments: | hfvars (list) |
| multiplier (scalar) |
Given a MIDAS list, produces a list of the same length holding high-frequency first differences. The second argument is optional and defaults to unity: it can be used to multiply the differences by some constant.
| Arguments: | hfvars (list) |
| multiplier (scalar) |
Given a MIDAS list, produces a list of the same length holding high-frequency log-differences. The second argument is optional and defaults to unity: it can be used to multiply the differences by some constant, for example one might give a value of 100 to produce (approximate) percentage changes.
| Arguments: | minlag (integer) |
| maxlag (integer) | |
| hfvars (list) |
Given a MIDAS list, hfvars, produces a list holding high-frequency lags minlag to maxlag. Use positive values for actual lags, negative for leads. For example, if minlag is –3 and maxlag is 5 then the returned list will hold 9 series: 3 leads, the contemporary value, and 5 lags.
Note that high-frequency lag 0 corresponds to the first high frequency period within a low frequency period, for example the first month of a quarter or the first day of a month.
| Arguments: | x (vector) |
| m (integer) | |
| prefix (string) |
Produces from the vector x a MIDAS list of m series, where m is the ratio of the frequency of observation for the variable in x to the base frequency of the current dataset. The value of m must be at least 3 and the length of x must be m times the length of the current sample range.
The names of the series in the returned list are constructed from the given prefix (which must be an ASCII string of 24 characters or less, and valid as a gretl identifier), plus one or more digits representing the sub-period of the observation. An error is flagged if any of these names duplicate names of existing objects.
| Arguments: | y (series) |
| lambda (scalar, optional) | |
| one-sided (boolean, optional) |
Returns the cycle component from application of the Hodrick–Prescott filter to series y. If the smoothing parameter, lambda, is not supplied then a data-based default is used, namely 100 times the square of the periodicity (100 for annual data, 1600 for quarterly data, and so on).
By default the filter is the usual two-sided version, but if the optional third argument is given with a non-zero value a one-sided variant (with no look-ahead) is computed in the manner of Stock and Watson (1999).
The most common use of the HP filter is detrending, but if it's the trend you are interested in that is easily obtained by subtraction, as in
series hptrend = y - hpfilt(y)
| Arguments: | a (scalar) |
| b (scalar) | |
| c (scalar) | |
| x (scalar or matrix) |
Returns the Gaussian hypergeometric function for the real argument x. Valid values for x are in the closed interval [–1, 1]. This function is very general, and reduces to a simpler function in some special cases, such as for example -log(1-x)/x for a=b=1 and c=2. See https://en.wikipedia.org/wiki/Hypergeometric_function for more details.
If x is a scalar, the return value will be scalar; otherwise, it will be a matrix the same size as x. For example,
a = hyp2f1(1, 1, 2, {-1, 0, 0.5})
print a
produces the following output:
a (1 x 3) 0.69315 1.0000 1.3863
| Arguments: | n (integer) |
| m (integer, optional) |
If m is omitted, returns an identity matrix of order n. Otherwise returns an n x m matrix with ones on the main diagonal and zeros elsewhere.
| Argument: | C (complex matrix) |
Returns a real matrix of the same dimensions as C, holding the imaginary part of the input matrix. See also Re.
| Arguments: | X (matrix) |
| skip_na (boolean, optional) |
Returns the row indices of the maxima of the columns of X. For columns containing NAs the result is also set to NA, unless the optional argument skip_na is nonzero, in which case the index for the maximum valid entry will be returned.
| Arguments: | X (matrix) |
| skip_na (boolean, optional) |
Returns the column indices of the maxima of the columns of X. For rows containing NAs the result is also set to NA, unless the optional argument skip_na is nonzero, in which case the index for the maximum valid entry will be returned.
| Arguments: | M (matrix) |
| x (scalar) |
Computes Prob(u'Au < x) for a quadratic form in standard normal variates, u, using the procedure developed by Imhof (1961).
If the first argument, M, is a square matrix it is taken to specify A, otherwise if it's a column vector it is taken to be the precomputed eigenvalues of A, otherwise an error is flagged.
See also pvalue.
| Arguments: | X (matrix) |
| skip_na (boolean, optional) |
Returns the row indices of the minima of the columns of X. For columns containing NAs the result is also set to NA, unless the optional argument skip_na is nonzero, in which case the index for the minimum valid entry will be returned.
| Arguments: | X (matrix) |
| skip_na (boolean, optional) |
Returns the column indices of the minima of the rows of X. For rows containing NAs the result is also set to NA, unless the optional argument skip_na is nonzero, in which case the index for the minimum valid entry will be returned.
| Arguments: | b (bundle) |
| key (string) |
Checks whether bundle b contains a data-item with name key. The value returned is an integer code for the type of the item: 0 for no match, 1 for scalar, 2 for series, 3 for matrix, 4 for string, 5 for bundle, 6 for array and 7 for list. The function typestr may be used to get the string corresponding to this code.
| Argument: | X (matrix) |
Returns the infinity-norm of X, that is, the maximum across the rows of X of the sum of absolute values of the row elements.
See also onenorm.
| Arguments: | L (list) |
| y (series) |
Returns the (1-based) position of y in list L, or 0 if y is not present in L.
The second argument may be given as the name of a series or alternatively as an integer ID number. If you know that a series of a certain name (say foo) exists, then you can call this function as, for example,
pos = inlist(L, foo)
Here you are, in effect, asking "Give me the position of series foo in list L (or 0 if it is not included in L)." However, if you are unsure whether a series of the given name exists, you should place the name in quotes:
pos = inlist(L, "foo")
In this case you are asking, "If there's a series named foo in L give me its position, otherwise return 0."
| Arguments: | s1 (string) |
| s2 (string) | |
| ign_case (boolean, optional) |
This is a boolean relative of strstr: it returns 1 if s1 contains s2, 0 otherwise. So the conditional expression
if instring("cattle", "cat")
is logically equivalent to, but more efficient than,
if strlen(strstr("cattle", "cat")) > 0
If the optional argument ign_case is nonzero, the search is case-insensitive. For example,
instring("Cattle", "cat")
returns 0, but
instring("Cattle", "cat", 1)
returns 1.
| Arguments: | S (array of strings) |
| test (string) | |
| simple (boolean, optional) |
Checks the elements of the strings array S for equality with test. By default, returns a column vector of length equal to the number of matches, holding the positions of the matches within the array—or an empty matrix in case of no matches.
Example:
strings S = defarray("A", "B", "C", "B")
eval instrings(S, "B")
2
4
If a non-zero value is given for the optional simple argument, the return value is a scalar: 1 if test is found in S, 0 otherwise. In this case the implementation is able to take a shortcut, so it's more efficient if you just want a boolean answer.
| Argument: | x (scalar, series or matrix) |
Returns the integer part of x, truncating the fractional part, or NA if the result cannot be represented as a 32-bit signed integer (does not lie in the interval [–2147483648, 2147483647]).
Note: int and floor differ in their effect for negative arguments: int(-3.5) gives –3, while floor(-3.5) gives –4. See also ceil, floor, round.
| Argument: | x (series) |
Returns a series in which missing values in x are imputed via linear interpolation, for time series data or in the time dimension of a panel dataset. Extrapolation is not performed; missing values are replaced only if they are both preceded and followed by valid observations.
| Argument: | A (square matrix) |
Returns the inverse of A. If A is singular or not square, an error message is produced and nothing is returned. Note that gretl checks automatically the structure of A and uses the most efficient numerical procedure to perform the inversion.
The matrix types gretl checks for are: identity; diagonal; symmetric and positive definite; symmetric but not positive definite; and triangular.
Note: it makes sense to use this function only if you plan to use the inverse of A more than once. If you just need to compute an expression of the form A-1B, you'll be much better off using the "division" operators \ and /. See chapter 17 of the Gretl User's Guide for details.
| Arguments: | d (string) |
| ... (see below) | |
| u (scalar, series or matrix) |
Inverse cumulative distribution function calculator. For a continuous distribution, returns x such that P(X <= x) = u, for u in the interval 0 to 1. For a discrete distribution (Binomial or Poisson), returns the smallest x such that P(X <= x) ≥ u.
The distribution of X is determined by the string d. Between the arguments d and u, zero or more additional scalar arguments are required to specify the parameters of the distribution, as follows.
Standard normal (c = z, n, or N): no extra arguments
Gamma (g or G): shape; scale
Student's t (t): degrees of freedom
Chi square (c, x, or X): degrees of freedom
Snedecor's F (f or F): df (num.); df (den.)
Binomial (b or B): probability; trials
Poisson (p or P): mean
Laplace (l or L): mean; scale
Standardized GED (E): shape
Non-central chi square (ncX): df, non-centrality parameter
Non-central F (ncF): df (num.), df (den.), non-centrality parameter
Non-central t (nct): df, non-centrality parameter
See also cdf, critical, pvalue.
| Argument: | x (scalar, series or matrix) |
Returns the inverse Mills ratio at x, that is the ratio between the standard normal density and the complement to the standard normal distribution function, both evaluated at x.
This function uses a dedicated algorithm which yields greater accuracy compared to calculation using dnorm and cnorm, but the difference between the two methods is appreciable only for very large negative values of x.
| Arguments: | A (positive definite matrix) |
| &logdet (reference to scalar, optional) |
Returns the inverse of the symmetric, positive definite matrix A. This function is slightly faster than inv for large matrices, since no check for symmetry is performed; for that reason it should be used with care.
If the optional argument &logdet is present, the corresponding scalar will contain on successful exit the log determinant of A. This may be convenient to have in some cases, for example in the context of the evaluation of a Gaussian log-likelihood, because the log determinant is a by-product of the inversion algorithm and retrieving it via the &logdet argument avoids extra computations.
Note: if you're interested in the inversion of a matrix of the form X'X, where X is a large matrix, it is preferable to compute it via the prime operator X'X rather than using the more general syntax X'*X. The former expression uses a specialized algorithm which has the double advantage of being more efficient computationally and of ensuring that the result will be free by construction of machine precision artifacts that may render it numerically non-symmetric.
| Arguments: | target (integer) |
| shock (integer) | |
| alpha (scalar between 0 and 1, optional) | |
| sys (bundle, optional) |
Provides estimated impulse response functions pertaining to a VAR or VECM, traced out over a certain forecast horizon. Without the final optional argument, this function works only when the last model estimated was a VAR or VECM. Alternatively, information on such a system can be saved as a bundle via the $system accessor and subsequently passed to irf.
The target and shock arguments take the form of 1-based indices of the endogenous variables in the system, with 0 taken to mean "all". The responses (expressed in the units of the target variable) are to an innovation of one standard deviation in the shock variable. If alpha is given a suitable positive value the estimates include a 1 – α confidence interval (so, for example, give 0.1 for a 90 percent interval).
The following code fragment illustrates usage. In the first example the matrix ir1 holds the responses of y1 to innovations in each of y1, y2 and y3 (point estimates only since alpha is omitted). In the second, ir2 holds the responses of all targets to an innovation in y2, with 90 percent confidence intervals. In this case the returned matrix will have 9 columns: each response path occupies 3 adjacent columns giving point estimate, lower bound and upper bound. The last example produces a matrix with 27 columns: 3 per response for each target times each shock.
var 4 y1 y2 y3 matrix ir1 = irf(1, 0) matrix ir2 = irf(0, 2, 0.1) matrix ir3 = irf(0, 0, 0.1)
The number of periods (rows) over which the response is traced is determined automatically based on the frequency of the data, but this can be overridden via the set command, as in set horizon 10.
When confidence intervals are produced they are derived via bootstrapping, with resampling of the original residuals. It is assumed that the lag order of the VAR or VECM is sufficient to eliminate serial correlation of the residuals. By default the number of bootstrap replications is 1999, but that can be adjusted via set, as in
set boot_iters 2999
| Argument: | x (series or vector) |
Returns the Internal Rate of Return for x, considered as a sequence of payments (negative) and receipts (positive). See also npv.
| Argument: | name (string) |
Tests whether name is the identifier for a complex matrix. The return value is one of the following:
NA: name does not identify a matrix.
0: name identifies a real matrix, composed entirely of regular floating-point numbers ("doubles", in C parlance).
1: name identifies a "nominally" complex matrix, composed of numbers with both a real and an imaginary part, but in which all imaginary parts are zero.
2: the matrix in question holds at least one "genuinely" complex value, with a non-zero imaginary part.
| Arguments: | y (series or vector) |
| panel-code (integer, optional) |
Without the optional second argument, returns 1 if y has a constant value over the current sample range (or over its entire length if y is a vector), otherwise 0.
The second argument is accepted only if the current dataset is a panel and y is a series. In that case a panel-code value of 0 calls for a check for time-invariance, while a value of 1 means check for cross-sectional invariance (that is, in each time period the value of y is the same for all groups).
If y is a series, missing values are ignored in checking for constancy.
| Argument: | name (string) |
If name is the identifier for a currently defined series, returns 1 if the series is marked as discrete-valued, otherwise 0. If name does not identify a series, returns NA.
| Argument: | x (series or vector) |
If all the values contained in x are 0 or 1 (or missing), returns the number of ones, otherwise 0.
| Argument: | x (scalar or matrix) |
Given a scalar argument, returns 1 if x is "Not a Number" (NaN), otherwise 0. Given a matrix argument, returns a matrix of the same dimensions with 1s in positions where the corresponding element of the input is NaN and 0s elsewhere.
| Arguments: | date (series) |
| &year (reference to series) | |
| &month (reference to series) | |
| &day (reference to series, optional) |
Given a series date holding dates in ISO 8601 "basic" format (YYYYMMDD), this function writes the year, month and (optionally) day components into the series named by the second and subsequent arguments. An example call, assuming the series dates contains suitable 8-digit values:
series y, m, d isoconv(dates, &y, &m, &d)
The nominal return value is 0 on successful completion; in case of failure an error is flagged.
| Arguments: | source (string or array of strings) |
| output (integer, optional) |
This function maps between the four designations for countries present in ISO 3166, namely
Country name
Alpha-2 code (two uppercase letters)
Alpha-3 code (three uppercase letters)
Numeric code (3 digits)
Given a country's designation in one form, the return value is its designation in the form (1 to 4) selected by the optional output argument or, if this argument is omitted, a default conversion as follows: when source is a country name the return value is the country's 2-letter code; otherwise the return value is the country name. Various valid calls are illustrated below in interactive form.
? eval isocountry("Bolivia")
BO
? eval isocountry("Bolivia", 3)
BOL
? eval isocountry("GB")
United Kingdom of Great Britain and Northern Ireland
? eval isocountry("GB", 3)
GBR
? strings S = defarray("ES", "DE", "SD")
? strings C = isocountry(S)
? print C
Array of strings, length 3
[1] "Spain"
[2] "Germany"
[3] "Sudan"
? matrix m = {4, 840}
? C = isocountry(m)
? print C
Array of strings, length 2
[1] "Afghanistan"
[2] "United States of America"
When source is in form 4 (numeric code) this can be given as a string or array of strings (for example, "032" for Argentina) or in numeric form. In the latter case source may be given as a series or vector, though an error will be flagged if any of the numbers are out of the range 0 to 999.
In all cases (even when output form 4 is selected) a string, or array of strings, is returned; if numeric values are required these may be obtained using atof. If source is not matched by any entry in the ISO 3166 table the return value is an empty string, in which case a warning is printed.
| Arguments: | ed (scalar, series or matrix) |
| as-string (boolean, optional) |
The argument ed is interpreted as an epoch day, which equals 1 for the first of January in the year 1 AD on the proleptic Gregorian calendar. The default return value (of the same type as ed) is an 8-digit number, or a series of such numbers, on the pattern YYYYMMDD (ISO 8601 "basic" format), giving the Gregorian calendar date corresponding to the epoch day.
If the optional second argument as-string is non-zero, the return value is not numeric but rather a string on the pattern YYYY-MM-DD (ISO 8601 "extended" format), or a string-valued series if ed is a series, or an array of strings if ed is a vector. For a more flexible means of obtaining string representations of epoch days, see strfday.
For the inverse function, see epochday; also see juldate.
| Arguments: | year (scalar or series) |
| month (scalar or series) | |
| day (scalar or series) |
Returns the ISO 8601 week number corresponding to the date(s) specified by the three arguments, or NA if the date is invalid. Note that all three arguments must be of the same type, either scalars (integers) or series.
ISO weeks are numbered from 01 to 53; most years have 52 weeks but on average 71 out of 400 years have 53 weeks. The ISO 8601 definition for week 01 is the week containing the year's first Thursday on the Gregorian calendar. For a full account see https://en.wikipedia.org/wiki/ISO_week_date.
An alternative call is also supported: if a single argument is given, it is taken to be a date (or series of dates) in ISO 8601 "basic" numeric format, YYYYMMDD. So the following two calls produce the same result, namely 13.
eval isoweek(2022, 4, 1) eval isoweek(20220401)
| Arguments: | S (symmetric matrix) |
| v (integer) |
Given S (a positive definite p x p scale matrix), returns a drawing from the Inverse Wishart distribution with v degrees of freedom, where v must not be smaller than p. The returned matrix is also p x p. The algorithm of Odell and Feiveson (1966) is used.
| Arguments: | buf (string) |
| path (string) | |
| &nread (reference to scalar, optional) |
The argument buf should be a JSON buffer, as may be retrieved from a suitable website via the curl function, and the path argument should be a JsonPath specification.
This function returns a string representing the data found in the buffer at the specified path. Data types of double (floating-point), int (integer) and string are supported. In the case of doubles or ints, their string representation is returned (using the "C" locale for doubles). If the object to which path refers is an array, the members are printed one per line in the returned string.
By default an error is flagged if path is not matched in the JSON buffer, but this behavior is modified if you pass the third, optional argument: in that case the argument retrieves a count of the matches and an empty string is returned if there are none. Example call:
ngot = 0 ret = jsonget(jbuf, "$.some.thing", &ngot)
However, an error is still flagged in case of a malformed query.
An accurate account of JsonPath syntax can be found at http://goessner.net/articles/JsonPath/. However, please note that the back-end for jsonget is provided by json-glib, which does not necessarily support all elements of JsonPath. Moreover, the exact functionality of json-glib may differ depending on the version you have on your system. See https://wiki.gnome.org/Projects/JsonGlib if you need details.
That said, the following operators should be available to jsonget:
root node, via the $ character
recursive descent operator: ..
wildcard operator: *
subscript operator: []
set notation operator, for example [i,j]
slice operator: [start:end:step]
| Arguments: | buf (string) |
| path (string, optional) |
The argument buf should be a JSON buffer, as may be retrieved from a suitable website via the curl function. The specification and effect of the optional path argument are described below.
The return value is a bundle whose structure basically mirrors that of the input: JSON objects become gretl bundles and JSON arrays become gretl arrays, each of which can hold strings, bundles or arrays. JSON "value" nodes become either members of bundles or elements of arrays; in the latter case numerical values are converted to strings using sprintf. Note that although the JSON specification allows arrays of mixed type these cannot be handled by jsongetb since gretl arrays must be of a single type.
The path argument can be used to limit the JSON elements included in the returned bundle. This is not a "JsonPath" as described in the help for jsonget; it is a simple construct subject to the following specification.
path is a slash-separated array of elements where slash ("/") indicates moving to one level "deeper" in the JSON tree represented by buf. A leading slash is allowed but not required; implicitly the path always starts at the root. No extraneous white-space characters should be included.
Each slash-separated element must take one of the following forms: (a) a single name, in which case only a JSON element whose name matches at the given structural level will be included; or (b) "*" (asterisk), in which case all elements at the given level are included; or (c) an array of comma-separated names, enclosed in braces ("{" and "}"), in which case only JSON elements whose names match one of the given names will be included.
See also the string-oriented jsonget; depending on your purpose one of these functions may be more helpful than the other.
| Arguments: | ed (scalar, series or matrix) |
| as-string (boolean, optional) |
This function works just like isodate except that on output the dates are relative to the Julian calendar rather than the Gregorian.
| Arguments: | x (series, list or matrix) |
| scale (scalar, optional) | |
| control (boolean, optional) |
Computes a kernel density estimate (or set of estimates) for the argument x, which may be a single series or vector or a list or matrix with more than column. The returned matrix has k + 1 columns, where k is the number of elements (series or columns) in x. The first column holds a set of evenly spaced abscissae and the rest hold the estimated density or densities at each of these points.
The formula used to compute the estimated density at each reference point, x, is
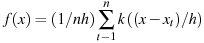
where n denotes the number of data points, h is a "bandwidth" parameter, and k() is the kernel function. The larger the value of the bandwidth parameter, the smoother the estimated density.
The optional scale parameter can be used to adjust the bandwidth relative to the default of 1.0, which corresponds to the rule of thumb proposed by Silverman (1986), namely
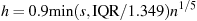
where s denotes the standard deviation of the data and IQR is the inter-quartile range. The control parameter acts as a boolean: 0 (the default) means that the Gaussian kernel is used; a non-zero value switches to the Epanechnikov kernel.
A plot of the results may be obtained using the gnuplot command, as illustrated below. Note that the column containing the abscissae should come last for plotting.
matrix d = kdensity(x) # if x has a single element gnuplot 2 1 --matrix=d --with-lines --fit=none # if x has two elements gnuplot 2 3 1 --matrix=d --with-lines --fit=none
| Arguments: | &kb (reference to bundle) |
| MSE (boolean, optional) |
Performs disturbance smoothing for a Kalman bundle previously set up by means of ksetup and returns 0 on successful completion or non-zero if numerical problems are encountered. The return value should be checked before making using of results.
On successful completion, the smoothed disturbances will be available as kb.smdist.
The optional MSE argument determines the contents of the kb.smdisterr key. If 0 or omitted, this matrix will contain the unconditional standard errors of the smoothed disturbances, which are normally used to compute the so-called auxiliary residuals. Otherwise, kb.smdisterr will contain the estimated root mean square deviations of the auxiliary residuals from their true value.
For more details see chapter 36 of the Gretl User's Guide.
See also ksetup, kfilter, ksmooth, ksimul.
| Argument: | &kb (reference to bundle) |
Performs a forward, filtering pass on a Kalman bundle previously set up by means of ksetup and returns 0 on successful completion or 1 if numerical problems are encountered.
On successful completion, the one-step-ahead prediction errors will be available as kb.prederr and the sequence of their covariance matrices as kb.pevar. Moreover, the key kb.llt gives access to a T-vector containing the log-likelihood by observation.
For more details see chapter 36 of the Gretl User's Guide.
See also kdsmooth, ksetup, ksmooth, ksimul.
| Arguments: | d (series or vector) |
| cens (series or vector, optional) |
Given a sample of duration data, d, possibly accompanied by a record of censoring status, cens, computes the Kaplan–Meier nonparametric estimator of the survival function (Kaplan and Meier, 1958). The returned matrix has three columns holding, respectively, the sorted unique values in d, the estimated survival function corresponding to the duration value in column 1 and the (large sample) standard error of the estimator, calculated via the method of Greenwood (1926).
If the cens series is given, the value 0 is taken to indicate an uncensored observation while a value of 1 indicates a right-censored observation (that is, the period of observation of the individual in question has ended before the duration or spell has been recorded as terminated). If cens is not given, it is assumed that all observations are uncensored. (Note: the semantics of cens may be extended at some point to cover other types of censoring.)
See also naalen.
| Arguments: | T (scalar) |
| trend (boolean) |
Returns a row vector containing critical values at the 10, 5 and 1 percent levels for the KPSS test for stationarity of a time series. T should give the number of observations and trend should be 1 if the test includes a trend, 0 otherwise.
The critical values given are based on response surfaces estimated in the manner set out by Sephton (Economics Letters, 1995). See also the kpss command.
| Arguments: | Y (series, matrix or list) |
| Z (scalar or matrix) | |
| T (scalar or matrix) | |
| Q (scalar or matrix) | |
| R (matrix, optional) |
Sets up a Kalman bundle, that is an object which contains all the information needed to define a linear state space model of the form

where Var(u) = R, and state transition equation

where Var(v) = Q.
Objects created via this function can be later used via the dedicated functions kfilter for filtering, ksmooth and kdsmooth for smoothing and ksimul for performing simulations.
The class of models that gretl can handle is in fact much wider than the one implied by the representation above: it is possible to have time-varying models, models with diffuse priors and exogenous variable in the measurement equation and models with cross-correlated innovations. For further details, see chapter 36 of the Gretl User's Guide.
See also kdsmooth, kfilter, ksmooth, ksimul.
| Arguments: | &kb (reference to bundle) |
| U (matrix) | |
| extra (boolean, optional) |
Uses a Kalman bundle previously set up by means of ksetup to perform simulation, the disturbances being taken from the matrix U. By default the returned matrix (which will have as many rows as U) contains simulated values of the observable(s), but if a non-zero value is given for extra the simulated state is also included. In the latter case each row holds the state first, then the observable(s).
For details see chapter 36 of the Gretl User's Guide.
See also ksetup, kfilter, ksmooth.
| Argument: | &kb (reference to bundle) |
Performs a fixed-point smoothing (backward) pass on a Kalman bundle previously set up by means of ksetup and returns 0 on successful completion or non-zero if numerical problems are encountered. The return value should be checked before making using of results.
On successful completion, the smoothed states will be available as kb.state and the sequence of their covariance matrices as kb.stvar. For more details see chapter 36 of the Gretl User's Guide.
See also ksetup, kdsmooth, kfilter, ksimul.
| Argument: | x (series) |
Returns the excess kurtosis of the series x, skipping any missing observations.
| Arguments: | p (scalar or vector) |
| y (series, list or matrix) | |
| bylag (boolean, optional) |
If the first argument is a scalar, generates lags 1 to p of the series y, or if y is a list, of all series in the list, or if y is a matrix, of all columns in the matrix. If p = 0 and y is a series or list, the maximum lag defaults to the periodicity of the data; otherwise p must be positive.
If a vector is given as the first argument, the lags generated are those specified in the vector. Common usage in this case would be to give p as, for example, seq(3,7), hence omitting the first and second lags. However, it is OK to give a vector with gaps, as in {3,5,7}, although the lags should always be given in ascending order.
In the case of list output, the generated variables are automatically named according to the template varname _ i where varname is the name of the original series and i is the specific lag. The original portion of the name is truncated if necessary, and may be adjusted in case of non-uniqueness in the set of names thus constructed.
When y is a list, or a matrix with more than one column, and the lag order is greater than 1, the default ordering of the terms in the return value is by variable: all lags of the first input series or column followed by all lags of the second, and so on. The optional third argument can be used to change this: if bylag is non-zero then the terms are ordered by lag: lag 1 of all the input series or columns, then lag 2 of all the series or columns, and so on.
See also mlag for use with matrices.
| Arguments: | y (series) |
| insample (boolean, optional) |
Returns the 1-based index of the last non-missing observation for the series y. By default the whole data range is examined, so if subsampling is in effect the value returned may be larger than the accessor $t2. But if a non-zero value is given for insample only the current sample range is considered. See also firstobs.
| Argument: | A (square matrix) |
Returns the natural log of the determinant of A, computed via the LU factorization. Note that this is more efficient than calling det and taking the log of the result. Moreover, in some cases ldet is able to return a valid result even if the determinant of A is numerically "infinite" (exceeds the C library's maximum double-precision number). See also rcond, cnumber.
| Argument: | y (series or list) |
Computes log differences; starting values are set to NA.
When a list is returned, the individual variables are automatically named according to the template ld_varname where varname is the name of the original series. The name is truncated if necessary, and may be adjusted in case of non-uniqueness in the set of names thus constructed.
| Arguments: | L (list) |
| b (vector) |
Computes a new series as a linear combination of the series in the list L. The coefficients are given by the vector b, which must have length equal to the number of series in L.
See also wmean.
| Argument: | x (series) |
Depends on having TRAMO installed. Returns a "linearized" version of the input series; that is, a series in which any missing values are replaced by interpolated values and outliers are adjusted. TRAMO's fully automatic mechanism is used; consult the TRAMO documentation for details.
Note that if the input series has no missing values and no values that TRAMO regards as outliers, this function will return a copy of the original series.
| Arguments: | y (series) |
| p (integer) |
Computes the Ljung–Box Q' statistic for the series y using lag order p, over the currently defined sample range. The lag order must be greater than or equal to 1 and less than the number of available observations.
This statistic may be referred to the chi-square distribution with p degrees of freedom as a test of the null hypothesis that the series y is not serially correlated. See also pvalue.
| Argument: | x (scalar, series or matrix) |
Returns the log of the gamma function of x. See also bincoeff, gammafun.
| Arguments: | x (scalar, series or matrix) |
| p (scalar, series or matrix) |
Returns the log of the multivariate gamma function of x with shape parameter p.
For its definition and properties, see https://dlmf.nist.gov/35.3 or https://en.wikipedia.org/wiki/Multivariate_gamma_function. See also lngamma.
| Arguments: | y (series) |
| x (series) | |
| d (integer, optional) | |
| q (scalar, optional) | |
| robust (boolean, optional) |
Performs locally-weighted polynomial regression and returns a series holding predicted values of y for each non-missing value of x. The method is as described by William Cleveland (1979).
The optional arguments d and q specify the order of the polynomial in x and the proportion of the data points to be used in local estimation, respectively. The default values are d = 1 and q = 0.5. The other acceptable values for d are 0 and 2. Setting d = 0 reduces the local regression to a form of moving average. The value of q must be greater than 0 and cannot exceed 1; larger values produce a smoother outcome.
If a non-zero value is given for the robust argument the local regressions are iterated twice, with the weights being modified based on the residuals from the previous iteration so as to give less influence to outliers.
See also nadarwat, and in addition see chapter 40 of the Gretl User's Guide for details on nonparametric methods.
| Argument: | x (scalar, series, matrix or list) |
Returns the natural logarithm of x; produces NA for non-positive values. Note: ln is an acceptable alias for log.
When a list is returned, the individual variables are automatically named according to the template l_varname where varname is the name of the original series. The name is truncated if necessary, and may be adjusted in case of non-uniqueness in the set of names thus constructed.
Note that in case of matrix input the function acts element by element. For the matrix logarithm function, see mlog.
| Argument: | x (scalar, series or matrix) |
Returns the base-10 logarithm of x; produces NA for non-positive values.
| Argument: | x (scalar, series or matrix) |
Returns the base-2 logarithm of x; produces NA for non-positive values.
| Argument: | x (scalar, series or matrix) |
Returns the logistic CDF of the argument x, that is, 1/(1 + e–x). If x is a matrix, the function is applied element by element.
| Argument: | specs (bundle) |
Solves a linear programming problem using the lpsolve library. See gretl-lpsolve.pdf for details and examples of usage.
| Argument: | A (matrix) |
Returns an n x n lower triangular matrix: the elements on and below the diagonal are equal to the corresponding elements of A; the remaining elements are zero.
See also upper.
| Arguments: | A (matrix) |
| demean (boolean, optional) |
Returns the long-run variance-covariance matrix of the columns of A. The data are first demeaned unless the second (optional) argument is set to zero. The kernel type and lag truncation parameter (window size) can be chosen before calling this function with the HAC-related options that the set command offers, such as hac_kernel, hac_lag, hac_prewhiten. See also the section on Time series data and HAC covariance matrices in chapter 22 of the Gretl User's Guide.
See also lrvar.
| Arguments: | y (series or vector) |
| k (integer, optional) | |
| mu (scalar, optional) |
Returns the long-run variance of y, calculated using a Bartlett kernel with window size k. If the second argument is omitted, or given a negative value, the window size defaults to the integer part of the cube root of the sample size.
For the variance calculation, the series y is centered around the optional parameter mu; if this is omitted or NA, the sample mean is used.
For a multivariate counterpart, see lrcovar.
| Arguments: | L (matrix) |
| B (matrix) |
Solves for x in AX = B, where L is the lower triangular Cholesky factor of the positive definite matrix A, satisfying LL' = A. Suitable L can be obtained using the cholesky function with A as argument.
The following two calculations should produce the same result (up to machine precision), but the first variant allows for reuse of a precomputed Cholesky factor and so should be substantially faster if you are solving repeatedly for given A and several values of B. The speed-up will be greater, the greater the dimension of A.
# variant 1 matrix L = cholesky(A) matrix X = Lsolve(L, B) # variant 2 matrix X = A \ B
| Arguments: | X (matrix) |
| prefix (string, optional) |
A convenience function for making a list of series using the columns of a suitable matrix as input. The row dimension of X must equal either the length of the current dataset or the number of observations in the current sample range.
The naming of the series in the returned list proceeds as follows. First, if the optional prefix argument is supplied, the series created from column i of X is named by appending i to the given string, as in myprefix1, myprefix2 and so on. Otherwise, if X has column names set (see cnameset) these names are used. Finally, if neither of the above conditions is satisfied, the names are column1, column2 and so on. Note that this policy may result in overwriting existing series; if you don't want that to happen, take charge of naming the columns explicitly via cnameset, or supply prefix.
Here is an illustrative example of usage:
matrix X = mnormal($nobs, 8) list L = mat2list(X, "xnorm") # or alternatively, if you don't need X as such list L = mat2list(mnormal($nobs, 8), "xnorm")
This will add to the dataset eight full-length series named xnorm1, xnorm2 and so on.
| Arguments: | x (scalar, series or matrix) |
| y (scalar, series or matrix, optional) |
This function has two primary modes plus a special case.
The first mode is activated if a single argument of type scalar, series or matrix is given: the return value is a scalar, the maximum valid value "within" the argument: if x is a series, its maximum value within the current sample range, or if x is a matrix, its greatest element, missing values being ignored. The case of a scalar argument is supported for the sake of completeness; you just get its value back.
The second mode is activated if two arguments are given. The arguments x and y must be of the same type, and must be scalars, series or matrices (and if they are matrices, they must be of the same dimensions). The return value is an object of the same type as the arguments, holding the "between" or "cross" maximum or maxima. If the arguments are scalars you get the greater of the two; if they're series you get a series holding the greater of the values of the two series at each observation in the current sample range; if they're matrices you get a matrix holding the greater of their elements in each row and column. For each of the pairwise comparisons if either term is missing the result is also a missing value.
This arises if a single list argument is given. The return value is a series, containing at each observation in the current sample range the greatest of the values of the series in the list at that observation.
See also min.
| Arguments: | X (matrix) |
| skip_na (boolean, optional) |
Returns a row vector containing the maxima of the columns of X. For columns containing NAs the result is also set to NA, unless the optional argument skip_na is nonzero, in which case the maximum valid entry will be returned.
| Arguments: | X (matrix) |
| skip_na (boolean, optional) |
Returns a column vector containing the maxima of the rows of X. For rows containing NAs the result is also set to NA, unless the optional argument skip_na is nonzero, in which case the maximum valid entry will be returned.
| Argument: | X (matrix) |
Computes a (Pearson) correlation matrix treating each column of X as a variable.
| Arguments: | X (matrix) |
| dfcorr (integer, optional) |
Computes a covariance matrix treating each column of X as a variable. The divisor is n – 1, where n is the number of rows of X, unless the optional second argument is supplied, in which case n – dfcorr is used.
| Arguments: | X (matrix) |
| u (vector, optional) | |
| w (vector, optional) | |
| p (integer) |
Returns the matrix covariogram for a T x k matrix X (typically containing regressors), an (optional) T -vector u (typically containing residuals), an (optional) (p+1)-vector of weights w, and a lag order p, which must be greater than or equal to 0.
The returned matrix is the sum for j from -p to p of w(|j|) * X(t)X(t-j)' * u(t)u(t-j), where X(t)' is the t-th row of X.
If u is given as null the u terms are omitted, and if w is given as null all the weights are taken to be 1.0.
For example, the following piece of code
set seed 123 X = mnormal(6,2) Lag = mlag(X,1) Lead = mlag(X,-1) print X Lag Lead eval X'X eval mcovg(X, , , 0) eval X'(X + Lag + Lead) eval mcovg(X, , , 1)
produces this output:
? print X Lag Lead X (6 x 2) -0.76587 -1.0600 -0.43188 0.30687 -0.82656 0.40681 0.39246 0.75479 0.36875 2.5498 0.28855 -0.55251 Lag (6 x 2) 0.0000 0.0000 -0.76587 -1.0600 -0.43188 0.30687 -0.82656 0.40681 0.39246 0.75479 0.36875 2.5498 Lead (6 x 2) -0.43188 0.30687 -0.82656 0.40681 0.39246 0.75479 0.36875 2.5498 0.28855 -0.55251 0.0000 0.0000 ? eval X'X 1.8295 1.4201 1.4201 8.7596 ? eval mcovg(X,,, 0) 1.8295 1.4201 1.4201 8.7596 ? eval X'(X + Lag + Lead) 3.0585 2.5603 2.5603 10.004 ? eval mcovg(X,,, 1) 3.0585 2.5603 2.5603 10.004
| Arguments: | x (series or list) |
| partial (boolean, optional) |
If x is a series, returns the (scalar) sample mean, skipping any missing observations.
If x is a list, returns a series y such that yt is the mean of the values of the variables in the list at observation t. By default the mean is recorded as NA if there are any missing values at t, but if you pass a non-zero value for partial any non-missing values will be used to form the statistic.
The following example illustrates the working of the function
open denmark.gdt eval mean(LRM) list L = dataset eval mean(L)
The first call will return the scalar mean value (scalar) of the series LRM, and the second one returns a series.
See also median, sum, max, min, sd, var.
| Arguments: | X (matrix) |
| skip_na (boolean, optional) |
Returns the means of the columns of X. If a non-zero value is given for the optional second argument missing values are ignored, otherwise the result is NA for any columns that contain missing values.
For example, the following piece of code
matrix m = mnormal(5, 2) m[1,2] = NA print m eval meanc(m)
produces this output:
? print m m (5 x 2) -0.098299 nan 1.1829 -1.2817 0.46037 -0.92947 1.4896 -0.91970 0.91918 0.47748 ? eval meanc(m) 0.79075 nan
See also meanr, sumc, maxc, minc, sdc, prodc.
| Arguments: | X (matrix) |
| skip_na (boolean, optional) |
Returns the means of the rows of X. If a non-zero value is given for the optional second argument missing values are ignored, otherwise the result is NA for any rows that contain missing values. See also meanc, sumr.
| Argument: | x (series or list) |
If x is a series, returns the (scalar) sample median, skipping any missing observations.
If x is a list, returns a series y such that yt is the median of the values of the variables in the list at observation t, or NA if there are any missing values at t.
The following example illustrates the working of the function
set verbose off open denmark.gdt eval median(LRM) list L = dataset series m = median(L)
The first call will return the scalar median value (scalar) of the series LRM, and the second one returns a series.
See also mean, sum, max, min, sd, var.
| Argument: | A (square matrix) |
Computes the matrix exponential of A. If A is a real matrix, algorithm 11.3.1 from Golub and Van Loan (1996) is used. If A is complex the algorithm uses eigendecomposition and A must be diagonalizable.
See also mlog.
| Arguments: | p (integer) |
| theta (vector) | |
| type (integer or string) |
Analytical derivatives for MIDAS weights. Let k denote the number of elements in the vector of hyper-parameters, theta. This function returns a p x k matrix holding the gradient of the vector of weights (as calculated by mweights) with respect to the elements of theta. The first argument represents the desired lag order and the last argument specifies the type of parameterization. See mweights for an account of the acceptable type values.
See also midasmult, mlincomb, mweights.
| Arguments: | mod (bundle) |
| cumulate (boolean) | |
| v (integer) |
Computes MIDAS multipliers. The mod argument must be a bundle containing a MIDAS model, as the one produced by the midasreg command and accessible via the $model keyword. The function returns a matrix with the implicit MIDAS multipliers for variable v in its first column and the corresponding standard errors in the second one. If the cumulate argument is nonzero, the multipliers are cumulated.
Note that the returned matrix is automatically endowed with appropriate row labels, so it is suitable to be used as the first argument to the modprint command. For example, the code
open gdp_midas.gdt list dIP = ld_indpro* smpl 1985:1 ; midasreg ld_qgdp 0 ; mds(dIP, 0, 6, 2) matrix ip_m = midasmult($model, 0, 1) modprint ip_m
produces the following output:
coefficient std. error z p-value
---------------------------------------------------------
dIP_0 0.343146 0.0957752 3.583 0.0003 ***
dIP_1 0.402547 0.0834904 4.821 1.43e-06 ***
dIP_2 0.176437 0.0673776 2.619 0.0088 ***
dIP_3 0.0601876 0.0621927 0.9678 0.3332
dIP_4 0.0131263 0.0259137 0.5065 0.6125
dIP_5 0.000965260 0.00346703 0.2784 0.7807
dIP_6 0.00000 0.00000 NA NA
See also mgradient, mweights, mlincomb.
| Arguments: | x (scalar, series or matrix) |
| y (scalar, series or matrix) |
Please see the help for max; this function works in exactly the same way except that it returns a minimum or minima.
| Arguments: | X (matrix) |
| skip_na (boolean, optional) |
Returns the minima of the columns of X. For columns containing NAs the result is also set to NA, unless the optional argument skip_na is nonzero, in which case the minimum valid entry will be returned.
| Arguments: | X (matrix) |
| skip_na (boolean, optional) |
Returns the minima of the rows of X. For rows containing NAs the result is also set to NA, unless the optional argument skip_na is nonzero, in which case the minimum valid entry will be returned.
| Argument: | x (scalar, series or list) |
Returns a binary variable holding 1 if x is NA. If x is a series, the comparison is done element by element; if x is a list of series, the output is a series with 1 at observations for which at least one series in the list has a missing value, and 0 otherwise. For example, the following code
nulldata 3 series x = normal() x[2] = NA series x_ismiss = missing(x) print x x_ismiss --byobs
sets a missing value at the second observation of x, and creates a new boolean series x_ismiss which identifies the missing observation
y y_ismiss 1 -1.551247 0 2 1 3 -2.244616 0
See also misszero, ok, zeromiss.
| Argument: | x (scalar, series or matrix) |
Converts NAs to zeros. If x is a series or matrix, the conversion is done element by element. For example, the following code
nulldata 3 series x = normal() x[2] = NA y = misszero(x) print x y --byobs
sets a missing value at the second observation of x, and creates a new series y for which the missing observation is replaced by zero:
x y 1 0.7355250 0.7355250 2 0.000 3 -0.2465936 -0.2465936
See also missing, ok, zeromiss.
| Arguments: | X (matrix) |
| p (scalar or vector) | |
| m (scalar, optional) |
Shifts up or down the rows of X. If p is a positive scalar, returns a matrix in which the columns of X are shifted down by p rows and the first p rows are filled with the value m. If p is a negative number, X is shifted up and the last rows are filled with the value m. If m is omitted, it is understood to be zero.
If p is a vector the operation described above is carried out for each element in p and the resulting matrices are joined horizontally. The following code illustrates this usage, for input X with two columns and input p calling for lags 1 and 2. Missing values are set to NA as opposed to the default of 0.
matrix X = mnormal(5, 2)
print X
eval mlag(X, {1, 2}, NA)
m (5 x 2)
1.5953 -0.070740
-0.52713 -0.47669
-2.2056 -0.28112
0.97753 1.4280
0.49654 0.18532
nan nan nan nan
1.5953 -0.070740 nan nan
-0.52713 -0.47669 1.5953 -0.070740
-2.2056 -0.28112 -0.52713 -0.47669
0.97753 1.4280 -2.2056 -0.28112
See also lags.
| Arguments: | hfvars (list) |
| theta (vector) | |
| type (integer or string) |
A convenience MIDAS function which combines lincomb with mweights. Given a list hfvars, it constructs a series which is a weighted sum of the elements of the list, the weights based on the vector of hyper-parameters theta and the type of parameterization: see mweights for details. Note that hflags is generally the best way to create a list suitable as the first argument to this function.
To be explicit, the call
series s = mlincomb(hfvars, theta, 2)
is equivalent to
matrix w = mweights(nelem(hfvars), theta, 2) series s = lincomb(hfvars, w)
but use of mlincomb saves on some typing and also some CPU cycles.
| Argument: | A (square matrix) |
Computes the matrix logarithm of A. The algorithm employed relies on eigendecomposition, which requires that A be diagonalizable. See also mexp.
| Arguments: | r (integer) |
| c (integer, optional) |
Returns a matrix with r rows and c columns, filled with standard normal pseudo-random variates. If omitted, the number of columns defaults to 1 (column vector). See also normal, muniform.
| Arguments: | Y (matrix) |
| X (matrix) | |
| &U (reference to matrix, or null) | |
| &V (reference to matrix, or null) |
Returns a k x n matrix of parameter estimates obtained by OLS regression of the T x n matrix Y on the T x k matrix X.
If the third argument is not null, the T x n matrix U will contain the residuals. If the final argument is given and is not null then the k x k matrix V will contain (a) the covariance matrix of the parameter estimates, if Y has just one column, or (b) X'X-1 if Y has multiple columns.
By default, estimates are obtained via Cholesky decomposition, with a fallback to QR decomposition if the columns of X are highly collinear. The use of SVD can be forced via the command set svd on.
| Arguments: | month (scalar or series) |
| year (scalar or series) | |
| weeklen (integer) |
Returns the number of (relevant) days in the specified month in the specified year, on the proleptic Gregorian calendar. The weeklen argument, which must equal 5, 6 or 7, gives the number of days in the week that should be counted (a value of 6 omits Sundays, and a value of 5 omits both Saturdays and Sundays).
The return value is a scalar if both month and year are scalars, otherwise a series.
For example, if you have a monthly dataset open, the call
series wd = monthlen($obsminor, $obsmajor, 5)
will return a series containing the number of working days for each month in the sample.
| Arguments: | x (series) |
| p (scalar) | |
| control (integer, optional) | |
| y0 (scalar, optional) |
Depending on the value of the parameter p, returns either a simple or an exponentially weighted moving average of the input series x.
If p > 1, a simple p-term moving average is computed, that is, the arithmetic mean of x from period t to t-p+1. If a non-zero value is supplied for the optional control parameter the MA is centered, otherwise it is "trailing". The optional y0 argument is ignored.
If p is a positive fraction, an exponential moving average is computed:
y(t) = p*x(t) + (1-p)*y(t-1)
By default the output series, y, is initialized using the first value of x, but the control parameter may be used to specify the number of initial observations that should be averaged to produce y(0). A zero value for control indicates that all the observations should be used. Alternatively, an initializer may be specified using the optional y0 argument; in that case the control argument is ignored.
| Arguments: | &object (reference to object) |
| op (string) |
Available only when gretl is in MPI mode (see gretl + MPI). Must be called by all processes. This function works like mpireduce except that all processes, not just the root process, get a copy of the "reduced" object in place of the original. It is therefore equivalent to mpireduce followed by a call to mpibcast, but more efficient.
Available only when gretl is in MPI mode (see gretl + MPI). Takes no arguments. Enforces synchronization of MPI processes: no process can continue beyond the barrier until it has been reached by all.
# nobody gets past until everyone gets here mpibarrier()
| Arguments: | &object (reference to object) |
| root (integer, optional) |
Available only when gretl is in MPI mode (see gretl + MPI). Must be called by all processes. Broadcasts the object argument, which must be given in pointer form, to all processes. The object in question (a matrix, bundle, scalar, array, string or list) must be declared in all processes prior to the broadcast. No process can continue beyond a call to mpibcast until all processes have successfully executed it.
By default "root", the source of the broadcast, is the MPI process with rank 0, but this can be adjusted via the optional second argument, which must be an integer from 0 to the number of MPI processes minus 1.
A simple example follows. On successful completion every process will have a copy of the matrix X defined at rank 0.
matrix X if $mpirank == 0 X = mnormal(T, k) endif mpibcast(&X)
| Argument: | src (integer) |
Available only when gretl is in MPI mode (see gretl + MPI). See mpisend, with which mpirecv must always be paired, for an explanation. The src argument specifies the rank of the process from which the object is to be received, in the range 0 to the number of MPI processes minus 1.
| Arguments: | &object (reference to object) |
| op (string) | |
| root (integer, optional) |
Available only when gretl is in MPI mode (see gretl + MPI). Must be called by all processes. This function gathers objects (scalars, matrices or arrays) of a specified name, given in pointer form, from all processes and "reduces" them to a single object at the root node.
The op argument specifies the reduction operation or method. The methods supported for scalars are sum, prod (product), max and min. For matrices the methods are sum, prod (Hadamard product), hcat (horizontal concatenation) and vcat (vertical concatenation). For arrays only acat (concatenation) is supported.
By default "root", the target of the reduction, is the MPI process with rank 0, but this can be adjusted via the optional third argument, which must be an integer from 0 to the number of MPI processes minus 1.
An example follows. On successful completion of the above, the root process will have a matrix X which is the sum of the matrices X at all processes.
matrix X X = mnormal(T, k) mpireduce(&X, sum)
| Arguments: | &M (reference to matrix) |
| op (string) | |
| root (integer, optional) |
Available only when gretl is in MPI mode (see gretl + MPI). Must be called by all processes. This function distributes chunks of a matrix in the root process to all processes. The matrix must be declared in all processes prior to the call to mpiscatter, and must be given in pointer form.
The op argument must be either byrows or bycols. Let q denote the quotient of the number of rows in the matrix to be scattered and the number of processes. In the byrows case root sends the first q rows to process 0, the next q to process 1, and so on. If there is a remainder from the division of rows it is added to the last allotment. The bycols case is exactly analogous but splitting of the matrix is by columns.
An example follows. If there are 4 processes, each one (including root) will each get a 2500 x 10 share of the original X as it existed in the root process. If you want to preserve the full matrix in the root process, it is necessary to make a copy of it before calling mpiscatter.
matrix X if $mpirank == 0 X = mnormal(10000, 10) endif mpiscatter(&X, byrows)
| Arguments: | object (object) |
| dest (integer) |
Available only when gretl is in MPI mode (see gretl + MPI). Sends the named object (a matrix, bundle, array, scalar, string or list) from the current process to the one identified by the integer dest (from 0 to the number of MPI processes minus 1).
A call to this function must always be paired with a call to mpirecv in the dest process, as in the following example which sends a matrix from rank 2 to rank 3.
if $mpirank == 2 matrix C = cholesky(A) mpisend(C, 3) elif $mpirank == 3 matrix C = mpirecv(2) endif
| Arguments: | Y (matrix) |
| X (matrix) | |
| &U (reference to matrix, or null) |
Works exactly as mols, except that the calculations are done in multiple precision using the GMP library.
By default GMP uses 256 bits for each floating point number, but you can adjust this using the environment variable GRETL_MP_BITS, e.g. GRETL_MP_BITS=1024.
| Arguments: | d (string) |
| p1 (scalar or matrix) | |
| p2 (scalar or matrix, conditional) | |
| p3 (scalar, conditional) | |
| rows (integer) | |
| cols (integer) |
With one exception (see below), this function works like randgen except that the return value is a matrix rather than a series. The initial arguments to this function (the number of which depends on the selected distribution) are as described for randgen, but they must be followed by two integers to specify the row and column dimensions of the desired random matrix. If p1 or p2 are given in matrix form they must have a number of elements equal to the product of rows and cols.
The exceptional case is the Dirichlet distribution. This is a multivariate distribution, and invoking mrandgen with "dir" as first parameter triggers special syntax: the second argument must be a k-element positive vector a, and the third a scalar r. The function will return an r x k matrix where each row is an independent draw from a Dirichlet distribution with parameter a.
The first example above calls for a column vector of length 50 holding draws from a continuous uniform distribution on [0,100]. The second example specifies a 20 x 20 random matrix with draws from the t distribution with 14 degrees of freedom; and the third returns a 30 x 4 matrix holding 30 draws from a specified Dirichlet distribution.
| Arguments: | fname (string) |
| import (boolean, optional) |
Reads a matrix from a file named fname. If the file name does not contain a full path specification, it will be looked for in several "likely" locations, beginning with the currently set workdir. However, if a non-zero value is given for the optional import argument, the input file is looked for in the user's "dot" directory. This is intended for use with the matrix-exporting functions offered in the context of the foreign command. In this case the fname argument should be a plain filename, without any path component.
Currently, the function recognizes four file formats:
These files are identified by the extension ".mat", and are fully compatible with the Ox matrix file format. If the filename has the suffix ".gz" it is assumed that gzip compression has been applied in writing the data. The file is assumed to be plain text, conforming to the following specification:
It starts with zero or more comments, defined as lines that start with the hash mark, #; such lines are ignored.
The first non-comment line contains two integers, separated by a tab character, indicating the number of rows and columns, respectively.
The columns are separated by tabs.
The decimal separator is the dot character, ".".
Files with the suffix ".bin" are assumed to be in binary format. The ".gz" suffix, for gzip compression, is also recognized. The first 19 bytes contain the characters gretl_binary_matrix, the next 8 bytes contain two 32-bit integers giving the number of rows and columns, and the remainder of the file contains the matrix elements as little-endian "doubles", in column-major order. If gretl is run on a big-endian system, the binary values are converted to little endian on writing, and converted to big endian on reading.
If the name of the file to be read has extension ".csv" the rules governing the format of the file are different, and more relaxed. In this case the actual data should not be preceded by a line giving the number of rows and columns. Gretl will try to figure out the delimiter (comma, semicolon or space) and do its best to import the matrix, allowing for use of comma as decimal separator if need be. Note that the delimiter should not be the tab character, on pain of confusing such files with those in gretl's "native" matrix format.
Files with extension ".gdt" or ".gdtb" are treated as gretl native data files, as created by the store command. In this case, the matrix returned contains the numerical values of the series of the dataset, arranged by column. Note that string-valued series are not read as such; the matrix will just contain their numeric encodings.
| Arguments: | X (matrix) |
| bycol (boolean, optional) |
Returns a matrix containing the rows of X in reverse order, or the columns in reverse order if the optional second argument has a non-zero value.
| Arguments: | Y (matrix) |
| X (matrix) | |
| R (matrix) | |
| q (column vector) | |
| &U (reference to matrix, or null) | |
| &V (reference to matrix, or null) |
Restricted least squares: returns a k x n matrix of parameter estimates obtained by least-squares regression of the T x n matrix Y on the T x k matrix X subject to the linear restriction RB = q, where B denotes the stacked coefficient vector. R must have kn columns; each row of this matrix represents a linear restriction. The number of rows in q must match the number of rows in R.
If the fifth argument is not null, the T x n matrix U will contain the residuals. If the final argument is given and is not null then the k x k matrix V will hold the restricted counterpart to the matrix X'X-1. The variance matrix of the estimates for equation i can be constructed by multiplying the appropriate sub-matrix of V by an estimate of the error variance for that equation.
| Arguments: | X (matrix) |
| r (integer) | |
| c (integer, optional) |
Rearranges the elements of X into a matrix with r rows and c columns. Elements are read from X and written to the target in column-major order. If X contains fewer than k = rc elements, the elements are repeated cyclically; otherwise, if X has more elements, only the first k are used.
If the third argument is omitted, c defaults to 1 if X is 1 x 1 otherwise to N/r where N is the total number of elements in X. However, if N is not an integer multiple of r an error is flagged.
See also cols, rows, unvech, vec, vech.
| Arguments: | X (matrix) |
| j (integer) |
Returns a matrix in which the rows of X are reordered by increasing value of the elements in column j. This is a stable sort: rows that share the same value in column j will not be interchanged.
| Arguments: | X (matrix) |
| v (scalar or matrix) | |
| bycol (boolean) |
Returns an array of matrices, the result of splitting X horizontally or vertically under the control of the arguments v and bycol. If bycol is nonzero, the matrix will be split by columns; otherwise, as per default, by rows.
The argument v can be either a vector or a scalar.
vector: must be of length equal to the relevant (row or column) dimension of X, and must contain positive integers. The greatest integer sets the length of the array that is returned. Each element of v indicates the array index of the matrix to which the corresponding row of X should be assigned.
scalar: the relevant dimension of X (row or column, as dictated by bycol) must be an exact multiple of the scalar value. X will be split in chunks with v rows or columns each.
In the following example we split a 4 x 3 matrix into three matrices: the first two rows are assigned to the first matrix; the second matrix is left empty; the third and fourth matrices gets row 3 and 4 of X, respectively
matrix X = {1,2,3; 4,5,6; 7,8,9; 10,11,12}
matrices M = msplitby(X, {1,1,3,4})
print M
The print statement gives
Array of matrices, length 4 [1] 2 x 3 [2] null [3] 1 x 3 [4] 1 x 3
The next example splits X evenly:
matrix X = {1,2,3; 4,5,6; 7,8,9; 10,11,12}
matrices MM = msplitby(X, 2)
print MM[1]
print MM[2]
which gives
? print MM[1] 1 2 3 4 5 6 ? print MM[2] 7 8 9 10 11 12
See flatten for the inverse operation.
| Arguments: | r (integer) |
| c (integer, optional) |
Returns a matrix with r rows and c columns, filled with uniform (0,1) pseudo-random variates. If omitted, the number of columns defaults to 1 (column vector). Note: the preferred method for generating a scalar uniform r.v. is to use the randgen1 function.
| Arguments: | p (integer) |
| theta (vector) | |
| type (integer or string) |
Returns a p-vector of MIDAS weights to be applied to p lags of a high-frequency series, based on the vector theta of hyper-parameters.
The type argument identifies the type of parameterization, which governs the required number of elements, k, in theta: 1 = normalized exponential Almon (k at least 1, typically 2); 2 = normalized beta with zero last (k = 2); 3 = normalized beta with non-zero last lag (k = 3); and 4 = Almon polynomial (k at least 1). Note that in the normalized beta case the first two elements of theta must be positive.
The type may be given as an integer code, as shown above, or by one of the following strings (respectively): nealmon, beta0, betan, almonp. If a string is used, it should be placed in double quotes. For example, the following two statements are equivalent:
W = mweights(8, theta, 2) W = mweights(8, theta, "beta0")
See also mgradient, midasmult, mlincomb.
| Arguments: | X (matrix) |
| fname (string) | |
| export (boolean, optional) |
Writes the matrix X to a file named fname. By default this file will be plain text; the first line will hold two integers, separated by a tab character, representing the number of rows and columns; on the following lines the matrix elements appear, in scientific notation, separated by tabs (one line per row). To avoid confusion on reading, files to be written in this format should be named with the suffix ".mat". See below for alternative formats.
If a file fname already exists, it will be overwritten. The nominal return value is 0 on successful completion; if writing fails an error is flagged.
The output file will be written in the currently set workdir, unless the filename string contains a full path specification. However, if a non-zero value is given for the export argument, the output file will be written into the user's "dot" directory, where it is accessible by default via the matrix-loading functions offered in the context of the foreign command. In this case a plain filename, without any path component, should be given for the second argument.
Matrices stored via the mwrite function in its default form can be easily read by other programs; see chapter 17 of the Gretl User's Guide for details.
Three mutually exclusive inflections of this function are available, as follows:
If fname has the suffix ".gz" then the file is written in the format described above but with gzip compression.
If fname has the suffix ".bin" then the matrix is written in binary format. In this case the first 19 bytes contain the characters gretl_binary_matrix, the next 8 bytes contain two 32-bit integers giving the number of rows and columns, and the remainder of the file contains the matrix elements as little-endian "doubles", in column-major order. If gretl is run on a big-endian system, the binary values are converted to little endian on writing, and converted to big endian on reading.
If fname has the suffix ".csv" then the matrix is written in comma-separated format, without a header line indicating the number of rows and columns to follow. This may be easier for third-party programs to handle, but it is not recommended if the matrix file is intended for reading by gretl.
Note that if the matrix file is to be read by a third-party program it is not advisable to use the gzip or binary options. But if the file is intended for reading by gretl the alternative formats save space, and the binary format allows for much faster reading of large matrices. The gzip format is not recommended for very large matrices, since decompression can be quite slow.
See also mread. And for writing a matrix to file as a dataset, see store.
| Arguments: | x (series or vector) |
| y (series or vector) |
Returns a matrix holding the cross tabulation of the values contained in x (by row) and y (by column). The two arguments should be of the same type (both series or both column vectors). It is generally expected (though not required) that the arguments will be discrete-valued, with fewer distinct values than observations. Otherwise the cross-tabulation may be very large and not very informative.
| Arguments: | d (series or vector) |
| cens (series or vector, optional) |
Given a sample of duration data, d, possibly accompanied by a record of censoring status, cens, computes the Nelson–Aalen nonparametric estimator of the hazard function (Nelson, 1972; Aalen, 1978). The returned matrix has three columns holding, respectively, the sorted unique values in d, the estimated cumulated hazard function corresponding to the duration value in column 1, and the standard error of the estimator.
If the cens series is given, the value 0 is taken to indicate an uncensored observation while a value of 1 indicates a right-censored observation (that is, the period of observation of the individual in question has ended before the duration or spell has been recorded as terminated). If cens is not given, it is assumed that all observations are uncensored. (Note: the semantics of cens may be extended at some point to cover other types of censoring.)
See also kmeier.
| Arguments: | y (series) |
| x (series) | |
| h (scalar, optional) | |
| LOO (boolean, optional) | |
| trim (scalar, optional) |
Computes the Nadaraya–Watson nonparametric estimator of the conditional mean of y given x. The return value is a series holding m(xi), the estimate of E(yi|xi) for each non-missing element of the series x.
The kernel function employed by this estimator is given by K = exp(-x2 / 2h) for |x| < T, and zero otherwise. (T = trimming parameter.)
The three optional arguments inflect the behavior of the estimator as described below.
The argument h can be used to control the bandwidth, a positive real number. This is usually small; larger values of h make m(x) smoother. A popular choice is to make h proportional to n-0.2. If h is omitted or set to zero, the bandwidth defaults to a data-determined value using the proportionality just mentioned but incorporating the dispersion of the x data as measured by the inter-quartile range or standard deviation; see chapter 40 of the Gretl User's Guide for more details.
"Leave-one-out" is a variant of the algorithm which omits the i-th observation when evaluating m(xi). This makes the Nadaraya–Watson estimator more robust numerically and is generally advised when the estimator is computed for inference purposes. This variant is not enabled by default, but is activated if a non-zero value is given for the LOO argument.
The trim argument can be used to control the degree of "trimming", which is imposed to prevent numerical problems when the kernel function is evaluated too far away from zero. This parameter is expressed as a multiple of h, the default value being 4. In some cases a value greater than 4 may be preferable. Again see chapter 40 of the Gretl User's Guide for details.
See also loess.
| Argument: | L (list, matrix, bundle or array) |
Returns the number of elements in the argument, which may be a list, a matrix, a bundle, an array or a string, but not a series. In the case of a string argument the number of bytes (which may not be equal to the number of characters in the string) is returned; see also strlen.
| Argument: | s (string) |
If an environment variable by the name of s is defined and has a numerical value, returns that value; otherwise returns NA. See also getenv.
| Argument: | buf (string) |
Returns a count of the complete lines (that is, lines that end with the newline character) in buf.
Example:
string web_page = readfile("http://gretl.sourceforge.net/")
scalar number = nlines(web_page)
print number
| Arguments: | &b (reference to matrix) |
| f (function call) | |
| maxfeval (integer, optional) |
Numerical maximization via the Nelder–Mead derivative-free simplex method. On input the vector b should hold the initial values of a set of parameters, and the argument f should specify a call to a function that calculates the (scalar) criterion to be maximized, given the current parameter values and any other relevant data. On successful completion, NMmax returns the maximized value of the criterion, and b holds the parameter values which produce the maximum.
The optional third argument may be used to set the maximum number of function evaluations; if it is omitted or set to zero the maximum defaults to 2000. As a special signal to this function the maxfeval value may be set to a negative number. In this case the absolute value is taken, and NMmax flags an error if the best value found for the objective function at the maximum number of function evaluations is not a local optimum. Otherwise non-convergence in this sense is not treated as an error.
If the object is in fact minimization, either the function call should return the negative of the criterion or alternatively NMmax may be called under the alias NMmin.
For more details and examples chapter 37 of the Gretl User's Guide. See also simann.
An alias for NMmax; if called under this name the function acts as a minimizer.
| Argument: | x (series or list) |
If x is a series, returns the number of non-missing observations for this series in the currently selected sample.
If x is a list, returns a series y such that yt is the count of the series in the list that have a non-missing value at observation t.
| Arguments: | μ (scalar) |
| σ (scalar) |
Generates a series of Gaussian pseudo-random variates with mean μ and standard deviation σ. If no arguments are supplied, standard normal variates N(0,1) are produced. The values are produced using the Ziggurat method (Marsaglia and Tsang, 2000).
See also randgen, mnormal, muniform.
| Arguments: | y (series or vector) |
| method (string, optional) |
Carries out one or more tests for normality of y. By default the Doornik–Hansen test is performed but the optional method argument can be used to select an alternative: use swilk to get the Shapiro–Wilk test, jbera for Jarque–Bera test, or lillie for the Lilliefors test. Or give all for the method argument to carry out all four tests.
The second argument may be given in either quoted or unquoted form. In the latter case, however, if the argument is the name of a string variable the value of the variable is substituted.
The returned matrix is 1 x 2 for a single test, or 4 x 2 if all tests are performed. Test statistics are found in the first column and p-values in the second. The test statistic does not follow the same distribution is all cases. For Doornik–Hansen and Jarque–Bera it is chi-square(2); for the other methods it is an idiosyncratic statistic whose p-value requires special calculation.
See also the normtest command.
| Arguments: | x (series or vector) |
| y (series or vector) | |
| method (string, optional) |
Calculates a measure of correlation between x and y using a nonparametric method. If given, the third argument should be either kendall (for Kendall's tau, version b, the default method) or spearman (for Spearman's rho).
The return value is a 3-vector holding the correlation measure plus a test statistic and p-value for the null hypothesis of no correlation. Note that if the sample size is too small the test statistic and/or p-value may be NaN (not a number, or missing).
See also corr for Pearson correlation.
| Arguments: | x (series or vector) |
| r (scalar) |
Returns the Net Present Value of x, considered as a sequence of payments (negative) and receipts (positive), evaluated at annual discount rate r, which must be expressed as a decimal fraction, not a percentage (0.05 rather than 5%). The first value is taken as dated "now" and is not discounted. To emulate an NPV function in which the first value is discounted, prepend zero to the input sequence.
Supported data frequencies are annual, quarterly, monthly, and undated (undated data are treated as if annual).
See also irr.
| Arguments: | &b (reference to matrix) |
| f (function call) | |
| g (function call, optional) | |
| h (function call, optional) |
Numerical maximization via the Newton–Raphson method. On input the vector b should hold the initial values of a set of parameters, and the argument f should specify a call to a function that calculates the (scalar) criterion to be maximized, given the current parameter values and any other relevant data. If the object is in fact minimization, this function should return the negative of the criterion. On successful completion, NRmax returns the maximized value of the criterion, and b holds the parameter values which produce the maximum.
The optional third and fourth arguments provide means of supplying analytical derivatives and an analytical (negative) Hessian, respectively. The functions referenced by g and h must take as their first argument a predefined matrix that is of the correct size to contain the gradient or Hessian, respectively, given in pointer form. They also must take the parameter vector as an argument (in pointer form or otherwise). Other arguments are optional. If either or both of the optional arguments are omitted, a numerical approximation is used.
For more details and examples see chapter 37 of the Gretl User's Guide. See also BFGSmax, fdjac.
An alias for NRmax; if called under this name the function acts as a minimizer.
| Argument: | A (matrix) |
Computes the right nullspace of A, via the singular value decomposition: the result is a matrix B such that the product AB is a zero matrix, except when A has full column rank, in which case an empty matrix is returned. Otherwise, if A is m x n, B will be n by (n – r), where r is the rank of A.
If A is not of full column rank, then the vertical concatenation of A and the transpose of B produces a full rank matrix.
Example:
A = mshape(seq(1,6),2,3)
B = nullspace(A)
C = A | B'
print A B C
eval A*B
eval rank(C)
Produces
? print A B C
A (2 x 3)
1 3 5
2 4 6
B (3 x 1)
-0.5
1
-0.5
C (3 x 3)
1 3 5
2 4 6
-0.5 1 -0.5
? eval A*B
-4.4409e-16
-4.4409e-16
? eval rank(C)
3
| Arguments: | b (column vector) |
| fcall (function call) | |
| d (scalar, optional) |
Calculates a numerical approximation to the Hessian associated with the n-vector b and the objective function specified by the argument fcall. The function call should take b as its first argument (either straight or in pointer form), followed by any additional arguments that may be needed, and it should return a scalar result. On successful completion numhess returns an n x n matrix holding the Hessian, which is exactly symmetric by construction.
The method used is Richardson extrapolation, with four steps. The optional third argument can be used to set the fraction d of the parameter value used in setting the initial step size; if this argument is omitted the default is d = 0.01.
Here is an example of usage:
matrix H = numhess(theta, myfunc(&theta, X))
Returns a series of consecutive integers, setting 1 at the start of the dataset. Note that the result is invariant to subsampling. This function is especially useful with time-series datasets. Note: you can write t instead of obs with the same effect.
See also obsnum.
| Argument: | t (scalar or vector) |
If t is a scalar, returns a single string, the observation label for observation t. The inverse function is provided by obsnum.
If t is a vector, returns an array of strings, the observation labels for the observations given by the elements of t.
In either case the t values must be integers, valid as 1-based indices of observations in the current dataset, otherwise an error is flagged.
| Argument: | s (string) |
Returns an integer corresponding to the observation specified by the string s. Note that the result is invariant to subsampling. This function is especially useful with time-series datasets. For example, the following code
open denmark k = obsnum(1980:1)
yields k = 25, indicating that the first quarter of 1980 is the 25th observation in the denmark dataset.
| Argument: | x (scalar, series, matrix or list) |
If x is a scalar, returns 1 if x is not NA, otherwise 0. If x is a series, returns a series with value 1 at observations with non-missing values and zeros elsewhere. If x is a list, the output is a series with 0 at observations for which at least one series in the list has a missing value, and 1 otherwise.
If x is a matrix the function returns a matrix of the same dimensions as x, with 1s in positions corresponding to finite elements of x and 0s in positions where the elements are non-finite (either infinities or not-a-number, as per the IEEE 754 standard).
See also missing, misszero, zeromiss. But note that these functions are not applicable to matrices.
| Argument: | X (matrix) |
Returns the 1-norm of the matrix X, that is, the maximum across the columns of X of the sum of absolute values of the column elements.
| Arguments: | r (integer) |
| c (integer, optional) |
Outputs a matrix with r rows and c columns, filled with ones. If omitted, the number of columns defaults to 1 (column vector).
| Argument: | y (series) |
Only applicable if the currently open dataset has a panel structure. Computes the forward orthogonal deviations for variable y.
This transformation is sometimes used instead of differencing to remove individual effects from panel data. For compatibility with first differences, the deviations are stored one step ahead of their true temporal location (that is, the value at observation t is the deviation that, strictly speaking, belongs at t – 1). That way one loses the first observation in each time series, not the last.
See also diff.
| Arguments: | d (string) |
| ... (see below) | |
| x (scalar, series or matrix) |
Probability density function calculator. Returns the density at x of the distribution identified by the code d. See cdf for details of the required (scalar) arguments. The distributions supported by the pdf function are the normal, Student's t, chi-square, F, Gamma, Beta, Exponential, Weibull, Laplace, Generalized Error, Binomial and Poisson. Note that for the Binomial and the Poisson what's calculated is in fact the probability mass at the specified point. For Student's t, chi-square, F the noncentral variants are supported too.
For the normal distribution, see also dnorm.
| Arguments: | x (series or vector) |
| bandwidth (scalar, optional) |
If only the first argument is given, computes the sample periodogram for the given series or vector. If the second argument is given, computes an estimate of the spectrum of x using a Bartlett lag window of the given bandwidth, up to a maximum of half the number of observations (T/2).
Returns a matrix with two columns and T/2 rows: the first column holds the frequency, ω, from 2π/T to π, and the second the corresponding spectral density.
| Arguments: | v (vector) |
| by_individual (boolean, optional) |
Only applicable if the currently open dataset has a panel structure. By default, performs the inverse operation of pshrink. That is, given a vector of length equal to the number of individuals in the current panel sample, it returns a series in which each value is repeated T times, for T the time-series length of the panel. The resulting series is therefore non-time varying.
If a non-zero value is given for by_individual, the length of v should equal T and repetition is across the individuals in the panel.
| Arguments: | y (series) |
| mask (series, optional) |
Only applicable if the current dataset has a panel structure. Returns a series holding the maxima of variable y for each cross-sectional unit (repeated for each time period).
If the optional second argument is provided then observations for which the value of mask is zero are ignored.
See also pmin, pmean, pnobs, psd, pxsum, pshrink, psum.
| Arguments: | y (series) |
| mask (series, optional) |
Only applicable if the current dataset has a panel structure. Returns a series holding the time-mean of variable y for each cross-sectional unit, the values being repeated for each period. Missing observations are skipped in calculating the means.
If the optional second argument is provided then observations for which the value of mask is zero are ignored.
See also pmax, pmin, pnobs, psd, pxmean, pxsum, pshrink, psum.
| Arguments: | y (series) |
| mask (series, optional) |
Only applicable if the current dataset has a panel structure. Returns a series holding the minima of variable y for each cross-sectional unit (repeated for each time period).
If the optional second argument is provided then observations for which the value of mask is zero are ignored.
See also pmax, pmean, pnobs, psd, pshrink, psum.
| Arguments: | y (series) |
| mask (series, optional) |
Only applicable if the current dataset has a panel structure. Returns a series holding the number of valid observations of variable y for each cross-sectional unit (repeated for each time period).
If the optional second argument is provided then observations for which the value of mask is zero are ignored.
See also pmax, pmin, pmean, psd, pshrink, psum.
| Argument: | a (vector) |
Finds the roots of a polynomial. If the polynomial is of degree p, the vector a should contain p + 1 coefficients in ascending order, i.e. starting with the constant and ending with the coefficient on xp.
The return value is a complex column vector of length p.
| Arguments: | y (series) |
| q (integer) |
Fits a polynomial trend of order q to the input series y using the method of orthogonal polynomials. The series returned holds the fitted values.
| Arguments: | X (matrix) |
| p (integer) | |
| covmat (boolean, optional) |
Let the matrix X be T x k, containing T observations on k variables. The argument p must be a positive integer less than or equal to k. This function returns a T x p matrix, P, holding the first p principal components of X.
The optional third argument acts as a boolean switch: if it is non-zero the principal components are computed on the basis of the covariance matrix of the columns of X (the default is to use the correlation matrix).
The elements of P are computed as the sum from i to k of Zti times vji, where Zti is the standardized value (or just the centered value, if the covariance matrix is used) of variable i at observation t and vji is the jth eigenvector of the correlation (or covariance) matrix of the Xis, with the eigenvectors ordered by decreasing value of the corresponding eigenvalues.
See also eigensym.
| Arguments: | X (matrix) |
| skip_na (boolean, optional) |
Returns the product of the elements of X, by column. If a non-zero value is given for the optional second argument missing values are ignored, otherwise the result is NA for any columns that contain missing values. Note that specifying skip_na is equivalent to treating missing values as if they were 1s.
See also prodr, meanc, sdc, sumc.
| Arguments: | X (matrix) |
| skip_na (boolean, optional) |
Returns the product of the elements of X, by row. If a non-zero value is given for the optional second argument missing values are ignored, otherwise the result is NA for any rows that contain missing values. Note that specifying skip_na is equivalent to treating missing values as if they were 1s.
| Arguments: | y (series) |
| mask (series, optional) |
Only applicable if the current dataset has a panel structure. Returns a series holding the sample standard deviation of variable y for each cross-sectional unit (with the values repeated for each time period). The denominator used is the sample size for each unit minus 1, unless the number of valid observations for the given unit is 1 (in which case 0 is returned) or 0 (in which case NA is returned).
If the optional second argument is provided then observations for which the value of mask is zero are ignored.
Note: this function makes it possible to check whether a given variable (say, X) is time-invariant via the condition max(psd(X)) == 0.
See also pmax, pmin, pmean, pnobs, pshrink, psum.
| Arguments: | A (symmetric matrix) |
| psdcheck (boolean, optional) |
Performs a generalized variant of the Cholesky decomposition of the matrix A, which must be positive semidefinite (but may be singular). If the input matrix is not square an error is flagged, but symmetry is assumed and not tested; only the lower triangle of A is read. The result is a lower-triangular matrix L which satisfies A = LL'. Indeterminate elements in the solution are set to zero.
To force a check on the positive semidefiniteness of A, give a non-zero value for the optional second argument. In that case an error is flagged if the maximum absolute value of A – LL' exceeds 1.0e-8. Such a check can also be performed manually:
L = psdroot(A) chk = maxc(maxr(abs(A - L*L')))
For the case where A is positive definite, see cholesky.
| Argument: | y (series) |
Only applicable if the current dataset has a panel structure. Returns a column vector holding the first valid observation for the series y for each cross-sectional unit in the panel, over the current sample range. If a unit has no valid observations for the input series it is skipped.
This function provides a means of compacting the series returned by functions such as pmax and pmean, in which a value pertaining to each cross-sectional unit is repeated for each time period.
See pexpand for the inverse operation.
| Arguments: | y (series) |
| mask (series, optional) |
This function is applicable only if the current dataset has a panel structure. It returns a series holding the sum over time of variable y for each cross-sectional unit, the values being repeated for each period. Missing observations are skipped in calculating the sums.
If the optional second argument is provided then observations for which the value of mask is zero are ignored.
See also pmax, pmean, pmin, pnobs, psd, pxsum, pshrink.
| Arguments: | c (character) |
| ... (see below) | |
| x (scalar, series or matrix) |
P-value calculator. Returns P(X > x), where the distribution of X is determined by the character c. Between the arguments c and x, zero or more additional arguments are required to specify the parameters of the distribution; see cdf for details. The distributions supported by the pvalue function are the standard normal, t, Chi square, F, gamma, binomial, Poisson, Exponential, Weibull, Laplace and Generalized Error.
See also critical, invcdf, urcpval, imhof.
| Arguments: | y (series) |
| mask (series, optional) |
Only applicable if the current dataset has a panel structure. Returns a series holding the cross-sectional mean of variable y for each time period, the values being repeated for each unit. Missing observations are skipped in calculating the means.
If the optional second argument is provided then observations for which the value of mask is zero are ignored.
See also pmax, pmean, pmin, pnobs, psd, pxsum, pshrink, psum.
| Arguments: | y (series) |
| mask (series, optional) |
Only applicable if the current dataset has a panel structure. Returns a series holding the number of valid observations of y in each time period (this count being repeated for each unit).
If the optional second argument is provided then observations for which the value of mask is zero are ignored.
Note that this function works in a different dimension from the pnobs function.
| Arguments: | y (series) |
| mask (series, optional) |
Only applicable if the current dataset has a panel structure. Returns a series holding the sum of the values of y for each cross-sectional unit in each period (the values being repeated for each unit).
If the optional second argument is provided then observations for which the value of mask is zero are ignored.
Note that this function works in a different dimension from the psum function.
| Arguments: | x (matrix) |
| A (symmetric matrix) |
Computes the quadratic form Y = xAx'. Using this function instead of ordinary matrix multiplication guarantees more speed and better accuracy, when A is a generic symmetric matrix. However, in the special case when A is the identity matrix, the simple expression x'x performs much better than qform(x',I(rows(x)).
In the special case when A is a diagonal matrix, the second argument can be given as a vector of the appropriate size, which is understood to contain the main diagonal of A. In this case, a more efficient algorithm is used.
If x and A are not conformable, or A is not symmetric, an error is returned.
| Arguments: | X2 (scalar) |
| df (integer) | |
| p1 (scalar) | |
| p2 (scalar) |
P-values for the test statistic from the QLR sup-Wald test for a structural break at an unknown point (see qlrtest), as per Bruce Hansen (1997).
The first argument, X2, denotes the (chi-square form of) the maximum Wald test statistic and df denotes its degrees of freedom. The third and fourth arguments represent, as decimal fractions of the overall estimation range, the starting and ending points of the central range of observations over which the successive Wald tests are calculated. For example if the standard approach of 15 percent trimming is adopted, you would set p1 to 0.15 and p2 to 0.85.
| Argument: | x (scalar, series or matrix) |
Returns quantiles for the standard normal distribution. If x is not between 0 and 1, NA is returned. See also cnorm, dnorm.
| Arguments: | X (matrix) |
| &R (reference to matrix, or null) | |
| &P (reference to matrix, or null) |
Computes the "thin" QR decomposition of an m x n matrix X with m ≥ n, such that X = QR where Q is an m x n orthogonal matrix and R is an n x n upper triangular matrix. The matrix Q is returned directly, while R can be retrieved via the optional second argument.
If the optional third argument is supplied the decomposition employs column pivoting, and on successful completion P holds the final ordering of the columns in the form of a row vector. If the columns are not in fact reordered P will compare equal to seq(1, n).
See also eigengen, eigensym, svd.
| Arguments: | n (integer) |
| type (integer, optional) | |
| a (scalar, optional) | |
| b (scalar, optional) |
Returns an n x 2 matrix for use with Gaussian quadrature (numerical integration). The first column holds the nodes or abscissae, the second the weights.
The first argument specifies the number of points (rows) to compute. The second argument codes for the type of quadrature: use 1 for Gauss–Hermite (the default); 2 for Gauss–Legendre; or 3 for Gauss–Laguerre. The significance of the optional parameters a and b depends on the selected type, as explained below.
Gaussian quadrature is a method of approximating numerically the definite integral of some function of interest. Let the function be represented as the product f(x)W(x). The types of quadrature differ in the specification of the component W(x): in the Hermite case this is exp(–x2); in the Laguerre case, exp(–x); and in the Legendre case simply W(x) = 1.
For each specification of W, one can compute a set of nodes, xi, and weights, wi, such that the sum from i=1 to n of wi f(xi) approximates the desired integral. The method of Golub and Welsch (1969) is used.
When the Gauss–Legendre type is selected, the optional arguments a and b can be used to control the lower and upper limits of integration, the default values being –1 and 1. (In Hermite quadrature the limits are fixed at minus and plus infinity, while in the Laguerre case they are fixed at 0 and infinity.)
In the Hermite case a and b play a different role: they can be used to replace the default form of W(x) with the (closely related) normal distribution with mean a and standard deviation b. Supplying values of 0 and 1 for these parameters, for example, has the effect of making W(x) into the standard normal pdf, which is equivalent to multiplying the default nodes by the square root of two and dividing the weights by the square root of π.
| Arguments: | y (series or matrix) |
| p (scalar or vector) |
If y is a series, returns the p-quantile for the series. For example, when p = 0.5, the median is returned.
If y is a matrix, returns a row vector containing the p-quantiles for the columns of y; that is, each column is treated as a series.
In addition, for matrix y an alternate form of the second argument is supported: p may be given as a vector. In that case the return value is an m x n matrix, where m is the number of elements in p and n is the number of columns in y.
Hyndman and Fan (1996) describe nine variant methods for calculating sample quantiles. The default method in gretl is the one they call Q6 (which is also the default in Python). Method Q7 (the default in R) or Q8 (the one recommended by Hyndman and Fan) can be selected instead via the set command, as in
set quantile_type Q7 # or Q8
For example, the code
set verbose off matrix x = seq(1,7)' set quantile_type Q6 printf "Q6: %g\n", quantile(x, 0.45) set quantile_type Q7 printf "Q7: %g\n", quantile(x, 0.45) set quantile_type Q8 printf "Q8: %g\n", quantile(x, 0.45)
produces the following output:
Q6: 3.6 Q7: 3.7 Q8: 3.63333
| Arguments: | d (string) |
| p1 (see below) | |
| p2 (scalar or series, conditional) | |
| p3 (scalar, conditional) |
All-purpose random number generator. The argument d is a string (in most cases just a single character) which specifies the distribution from which the pseudo-random numbers should be drawn. The arguments p1 to p3 specify the parameters of the selected distribution; the number of such parameters (and, in some cases, their nature) depends on the distribution.
For distributions other than the beta-binomial and the generic discrete, the parameters p1 and (if applicable) p2 may be given as either scalars or series: if they are given as scalars the output series is identically distributed, while if a series is given for p1 or p2 the distribution is conditional on the parameter value at each observation.
The two special cases have the following requirements:
beta-binomial: all three parameters must be scalar.
generic discrete: a single parameter is wanted, namely a k-vector whose elements represent the probabilities for an integer-valued random variable with support from 1 to k.
Specifics are given below: the string code for each distribution is shown in parentheses, followed by the interpretation of the arguments p1 and, where applicable, p2 and p3.
Uniform (continuous) (u or U): minimum, maximum
Uniform (discrete) (i): minimum, maximum
Normal (z, n, or N): mean, standard deviation
Student's t (t): degrees of freedom
Chi square (c, x, or X): degrees of freedom
Snedecor's F (f or F): df (num.), df (den.)
Gamma (g or G): shape, scale
Binomial (b or B): probability, number of trials
Poisson (p or P): mean
Exponential (exp): scale
Logistic (lgt or s): location, scale
Weibull (w or W): shape, scale
Laplace (l or L): mean, scale
Generalized Error (E): shape
Beta (beta): shape1, shape2
Beta-Binomial (bb): trials, shape1, shape2
Generic discrete (disc): probabilities
See also normal, uniform, mrandgen, randgen1.
| Arguments: | d (character) |
| p1 (scalar) | |
| p2 (scalar, conditional) |
Works like randgen except that the return value is a scalar rather than a series.
The first example above calls for a value from the standard normal distribution, while the second specifies a drawing from the Gamma distribution with shape 3 and scale 2.5.
See also mrandgen.
| Arguments: | min (integer) |
| max (integer) |
Returns a pseudo-random integer in the closed interval [min, max]. See also randgen.
| Arguments: | n (integer) |
| k (integer, optional) |
If only the first argument is given, returns a row vector containing a random permutation of the integers from 1 to n, without repetition of elements. If the second argument is given it must be a positive integer in the range 1 to n; in this case the function returns a row vector containing k integers selected randomly from 1 to n without replacement.
If you wish to sample k rows from a matrix X with n rows (without replacement), that can be accomplished as shown below:
matrix S = X[randperm(n, k),]
And if you wish to preserve the original order of the rows in the sample:
matrix S = X[sort(randperm(n, k)),]
See also resample for resampling with replacement.
| Argument: | n (integer) |
Returns a random string of length n bytes. The string includes the numerals 0 to 9 and the lower-case letters a to f with equal probability, and is interpretable as a hexadecimal integer. Intended usage is as a unique identifier. For example, with n = 16 the string will one of over 1019 possibilities and so unique with probability close to 1.
| Arguments: | X (matrix) |
| tol (scalar, optional) |
Returns the rank of the r x c matrix X, numerically computed via the singular value decomposition.
The result of this operation is the number of singular values of X that are found to be numerically greater than 0. The tol optional parameter can be used for tweaking this aspect. Singular values are considered to be non-zero if they are greater than m × tol × s, where m is the greater of r and c and s is the largest singular value. If the second argument is omitted tol is set to machine epsilon (see $macheps). In some cases, you may want to set tol to a larger value (eg 1.0e-9) in order to avoid overestimating the rank of X, which may lead to numerically unstable results.
See also svd.
| Argument: | y (series or vector) |
Returns a series or vector with the ranks of y. The rank for observation i is the number of elements that are less than yi plus one half the number of elements that are equal to yi. (Intuitively, you may think of chess points, where victory gives you one point and a draw gives you half a point.) One is added so the lowest rank is 1 instead of 0.
| Argument: | A (square matrix) |
Returns the reciprocal condition number for A with respect to the 1-norm. In many circumstances, this is a better measure of the sensitivity of A to numerical operations such as inversion than the determinant.
The value is computed as the reciprocal of the product, 1-norm of A times 1-norm of A-inverse.
| Argument: | C (complex matrix) |
Returns a real matrix of the same dimensions as C, holding the real part of the input matrix. See also Im.
| Arguments: | fname (string) |
| codeset (string, optional) |
If a file by the name of fname exists and is readable, returns a string containing the content of this file, otherwise flags an error. If fname does not contain a full path specification, it will be looked for in several "likely" locations, beginning with the currently set workdir. If the file in question is gzip-compressed, this is handled transparently.
If fname starts with the identifier of a supported internet protocol (http://, ftp:// or https://), libcurl is invoked to download the resource. See also curl for more elaborate downloading operations.
If the text to be read is not encoded in UTF-8, gretl will try recoding it from the current locale codeset if that is not UTF-8, or from ISO-8859-15 otherwise. If this simple default does not meet your needs you can use the optional second argument to specify a codeset. For example, if you want to read text in Microsoft codepage 1251 and that is not your locale codeset, you should give a second argument of "cp1251".
Examples:
string web_page = readfile("http://gretl.sourceforge.net/")
print web_page
string current_settings = readfile("@dotdir/.gretl2rc")
print current_settings
Also see the sscanf and getline functions.
| Arguments: | s (string, strings array or string-valued series) |
| match (string) | |
| repl (string) |
If s is a single string, returns a copy of s in which all occurrences of the pattern match are replaced using repl. The arguments match and repl are interpreted as Perl-style regular expressions. If s is an array of strings or string-valued series this operation is performed on each string in the array or series.
See also strsub for simple substitution of literal strings.
| Argument: | fname (string) |
If a file by the name of fname exists and is writable by the user, this function removes (deletes) the file and returns 0. If there is no such file or for some reason the file cannot be deleted, a non-zero error code is returned.
If fname does not specify a full path, it is taken to be relative to the current workdir.
| Arguments: | x (series or matrix) |
| find (scalar or vector) | |
| subst (scalar or vector) |
Replaces each element of x equal to the i-th element of find with the corresponding element of subst.
If find is a scalar, subst must also be a scalar. If find and subst are both vectors, they must have the same number of elements. But if find is a vector and subst a scalar, then all matches will be replaced by subst.
Example:
a = {1,2,3;3,4,5}
find = {1,3,4}
subst = {-1,-8, 0}
b = replace(a, find, subst)
print a b
produces
a (2 x 3)
1 2 3
3 4 5
b (2 x 3)
-1 2 -8
-8 0 5
| Arguments: | x (series or matrix) |
| blocksize (integer, optional) | |
| draws (integer, optional) |
The initial description of this function pertains to cross-sectional or time-series data; see below for the case of panel data.
Resamples from x with replacement. In the case of a series argument, each value of the returned series, yt, is drawn from among all the values of xt with equal probability. When a matrix argument is given, each row of the returned matrix is drawn from the rows of x with equal probability. See also randperm for sampling rows from a matrix without replacement.
The optional argument blocksize represents the block size for resampling by moving blocks. If this argument is given it should be a positive integer greater than or equal to 2. The effect is that the output is composed by random selection with replacement from among all the possible contiguous sequences of length blocksize in the input. (In the case of matrix input, this means contiguous rows.) If the length of the data is not an integer multiple of the block size, the last selected block is truncated to fit.
By default the number of resampled observations in the output is equal to that in the input—if x is a series, the length of the current sample range; if x is a matrix, its number of rows. In the matrix case only this can be adjusted via the optional third argument, which must be a positive integer. Note that if blocksize is greater than 1, draws refers to the number of individual observations, not the number of blocks.
If the argument x is a series and the dataset takes the form of a panel, resampling by moving blocks is not supported. The basic form of resampling is supported, but has this specific interpretation: the data are resampled "by individual". Suppose you have a panel in which 100 individuals are observed over 5 periods. Then the returned series will again be composed of 100 blocks of 5 observations: each block will be drawn with equal probability from the 100 individual time series, with the time-series order preserved.
| Arguments: | color1 (string) |
| color2 (string) | |
| f (matrix) | |
| plot (boolean, optional) |
Given two colors and a vector f of length n containing values in [0,1], this function returns an array of n strings, element i of which holds the hexadecimal RGB code for a mixture of the form (1-fi) × color1 + fi × color2. The weighted average is taken over the Red, Green and Blue channels of the input colors.
The color arguments can be specified by names known to gnuplot, or as hexadecimal values in the form 0xrrggbb or #rrggbb. Hex values in the first of these forms may be given numerically, otherwise strings are needed. If a non-zero value is given for the plot argument, a plot that shows the color mixtures is produced.
This function offers a means of generating a set of related colors for plotting purposes, the primary use case being specification of multiple bands in a plot (for example, to indicate confidence intervals at more than one level). Three examples follow: the first produces successive lightenings of an initial blue; the second progressive darkenings of a pink shade; and the third a transition from red to yellow.
f = {0, 0.5, 0.75, 0.875, 0.9375}
mixes = rgbmix(0x1b43dc, "white", f, 1)
print mixes
f = {0, 0.1, 0.2, 0.3, 0.4}
rgbmix(0xefd0d3, "black", f, 1)
f = {0, 0.2, 0.4, 0.6, 0.8, 1}
rgbmix("red", "yellow", f, 1)
The output from the print command in the first example is
[1] "0x1b43dc" [2] "0x8da1ee" [3] "0xc6d0f6" [4] "0xe2e8fb" [5] "0xf1f3fd"
| Argument: | x (scalar, series or matrix) |
Rounds to the nearest integer. Note that when x lies halfway between two integers, rounding is done "away from zero", so for example 2.5 rounds to 3, but round(-3.5) gives –4. This is a common convention in spreadsheet programs, but other software may yield different results. See also ceil, floor, int.
| Arguments: | M (matrix) |
| r (integer, optional) |
If the r argument is given, retrieves the name for row r of matrix M. If M has no row names attached the value returned is an empty string; if r is out of bounds for the given matrix an error is flagged.
If no second argument is given, retrieves an array of strings holding the row names from M, or an empty array if the matrix does not have row names attached.
Example:
matrix A = { 11, 23, 13 ; 54, 15, 46 }
rnameset(A, "First Second")
string name = rnameget(A, 2)
print name
See also rnameset.
| Arguments: | M (matrix) |
| S (array of strings or list) |
Attaches names to the rows of the m x n matrix M. If S is a named list, the names are taken from the names of the listed series; the list must have m members. If S is an array of strings, it should contain m elements. A single string is also acceptable as the second argument; in that case it should contain m space-separated substrings.
The nominal return value is 0 on successful completion; in case of failure an error is flagged. See also cnameset.
Example:
matrix M = {1, 2; 2, 1; 4, 1}
strings S = array(3)
S[1] = "Row1"
S[2] = "Row2"
S[3] = "Row3"
rnameset(M, S)
print M
| Argument: | X (matrix) |
Returns the number of rows of the matrix X. See also cols, mshape, unvech, vec, vech.
| Arguments: | A (complex matrix) |
| &Z (reference to matrix, or null) | |
| &w (reference to matrix, or null) |
Performs the Schur decomposition of the complex matrix A, returning a complex upper triangular matrix T. If the second argument is given and is not null it retrieves a complex matrix Z holding the Schur vectors associated with A and T, such that A = ZTZH. If the third argument is given it retrieves the eigenvalues of A in a complex column vector.
| Arguments: | x (series or list) |
| partial (boolean, optional) |
If x is a series, returns the (scalar) sample standard deviation, skipping any missing observations.
If x is a list, returns a series y such that yt is the sample standard deviation of the values of the series in the list at observation t. By default the standard deviation is recorded as NA if there are any missing values at t, but if you pass a non-zero value for partial any non-missing values will be used to form the statistic.
See also var.
| Arguments: | X (matrix) |
| df (scalar, optional) | |
| skip_na (boolean, optional) |
Returns the standard deviations of the columns of X. If df is positive it is used as the divisor for the column variances, otherwise the divisor is the number of rows in X (that is, no degrees of freedom correction is applied). If a non-zero value is given for the optional third argument missing values are ignored, otherwise the result is NA for any columns that contain missing values.
| Argument: | y (series or list) |
Computes seasonal differences: y(t) - y(t-k), where k is the periodicity of the current dataset (see $pd or $panelpd). Starting values are set to NA.
When a list is returned, the individual variables are automatically named according to the template sd_varname where varname is the name of the original series. The name is truncated if necessary, and may be adjusted in case of non-uniqueness in the set of names thus constructed.
| Arguments: | baseline (integer, optional) |
| center (boolean, optional) |
Applicable only if the dataset has a time-series structure with periodicity greater than 1. Returns a list of dummy variables coding for the period or season, named S1, S2 and so on.
The optional baseline argument can be used to exclude one period from the set of dummies. For example, if you give a baseline value of 1 with quarterly data the returned list will hold dummies for quarters 2, 3 and 4 only. If this argument is omitted or set to zero a full set of dummies is generated; if non-zero, it must be an integer from 1 to the periodicity of the data.
The center argument, if non-zero, calls for the dummies to be centered; that is, to have their population mean subtracted. For example, with quarterly data centered seasonals will have values –0.25 and 0.75 rather than 0 and 1.
With weekly data the precise effect depends on whether the data are dated or not. If they are dated, up to 53 seasonals are created, based on the ISO 8601 week number (see isoweek); if not, the maximum number of series is 52 (and over a long time span the "seasonals" will drift out of phase with the calendar year). In the dated weekly case, if you wish to create monthly seasonals this can be done as follows:
series month = $obsminor list months = dummify(month)
See dummify for details.
| Arguments: | A (matrix) |
| b (row vector) |
Selects from A only the columns for which the corresponding element of b is non-zero. b must be a row vector with the same number of columns as A.
See also selifr.
| Arguments: | A (matrix) |
| b (column vector) |
Selects from A only the rows for which the corresponding element of b is non-zero. b must be a column vector with the same number of rows as A.
| Arguments: | a (scalar) |
| b (scalar) | |
| k (scalar, optional) |
Given only two arguments, returns a row vector filled with values from a to b with an increment of 1, or a decrement of 1 if a is greater than b.
If the third argument is given, returns a row vector containing a sequence of values starting with a and incremented (or decremented, if a is greater than b) by k at each step. The final value is the largest member of the sequence that is less than or equal to b (or mutatis mutandis for a greater than b). The argument k must be positive.
| Arguments: | b (bundle) |
| key (string) | |
| note (string) |
Sets a descriptive note for the object identified by key in the bundle b. This note will be shown when the print command is used on the bundle. This function returns 0 on success or non-zero on failure (for example, if there is no object in b under the given key).
| Argument: | x (scalar, series or matrix) |
Returns the sign function of x; that is, 0 if x is zero, 1 if x is positive, –1 if x is negative, or NA if x is Not a Number.
| Arguments: | &b (reference to matrix) |
| f (function call) | |
| maxit (integer, optional) |
Implements simulated annealing, which may be helpful in improving the initialization for a numerical optimization problem.
On input the first argument holds the initial value of a parameter vector and the second argument specifies a function call which returns the (scalar) value of the maximand. The optional third argument specifies the maximum number of iterations (which defaults to 1024). On successful completion, simann returns the final value of the maximand and b holds the associated parameter vector.
For more details and an example see chapter 37 of the Gretl User's Guide. See also BFGSmax, NRmax.
| Argument: | x (scalar, series or matrix) |
Returns the sine of x. See also cos, tan, atan.
| Argument: | x (scalar, series or matrix) |
Returns the hyperbolic sine of x.
| Argument: | x (series) |
Returns the skewness value for the series x, skipping any missing observations.
| Argument: | ns (scalar) |
Not of any direct use for econometrics, but can be useful for testing parallelization methods. This function simply causes the current thread to "sleep"—that is, do nothing—for ns seconds. The argument must be non-negative. On wake-up, the function returns 0.
| Arguments: | startobs (string) |
| endobs (string) | |
| pd (integer) |
Returns the number of observations from startobs to endobs (inclusive) for time-series data with frequency pd.
The first two arguments should be given in the form preferred by gretl for annual, quarterly or monthly data—for example, 1970, 1970:1 or 1970:01 for each of these frequencies, respectively—or as ISO 8601 dates, YYYY-MM-DD.
The pd argument must be 1, 4 or 12 (annual, quarterly, monthly); one of the daily frequencies (5, 6, 7); or 52 (weekly). If pd equals 1, 4 or 12, then ISO 8601 dates are acceptable for the first two arguments if they indicate the start of the period in question. For example, 2015-04-01 is acceptable in place of 2015:2 to represent the second quarter of 2015.
If you already have a dataset of frequency pd in place, with a sufficient range of observations, then the result of this function could easily be emulated using obsnum. The advantange of smplspan is that you can calculate the number of observations without having a suitable dataset (or any dataset) in place. An example follows:
scalar T = smplspan("2010-01-01", "2015-12-31", 5)
nulldata T
setobs 5 2010-01-01
This produces:
? scalar T = smplspan("2010-01-01", "2015-12-31", 5)
Generated scalar T = 1565
? nulldata T
periodicity: 1, maxobs: 1565
observations range: 1 to 1565
? setobs 5 2010-01-01
Full data range: 2010-01-01 - 2015-12-31 (n = 1565)
After the above, you can be confident that the last observation in the dataset created via nulldata will be 2015-12-31. Note that the number 1565 would have been rather tricky to compute otherwise.
| Argument: | x (series, vector or strings array) |
Sorts x in ascending order. Observations with missing values are skipped if x is a series, but sorted to the end if x is a vector. See also dsort, values. For matrices specifically, see msortby.
| Arguments: | y1 (series) |
| y2 (series) |
Returns a series containing the elements of y2 sorted by increasing value of the first argument, y1. See also sort, ranking.
| Arguments: | X (matrix) |
| mode (integer) | |
| &J (reference to matrix, or null) |
Calculates the spherical coordinates representation of a correlation matrix, or its inverse, depending on the value of the mode parameter.
When mode is 0 or omitted, X is assumed to be an n x n correlation matrix. The returned value will be a vector with n(n-1)/2 elements between 0 and π. In this mode the reference to J is ignored.
When mode is 1 or 2 the inverse transformation is performed, so X must be a vector with n(n-1)/2 elements between 0 and π. The return value is the correlation matrix R if mode equals 1, or its Cholesky factor K if mode equals 2. The optional pointer to matrix J, if present, retrieves the Jacobian of vech(R) or vech(K) with respect to X.
Note that the spherical coordinates representation makes it very easy to compute the log-determinant of the correlation matrix R:
omega = sphericorr(X) log_det = 2 * sum(log(sin(omega)))
| Arguments: | format (string) |
| ... (see below) |
The returned string is constructed by printing the values of the trailing arguments, indicated by the dots above, under the control of format. It is meant to give you great flexibility in creating strings. The format is used to specify the precise way in which you want the arguments to be printed.
In general, format must be an expression that evaluates to a string, but in most cases will just be a string literal (an alphanumeric sequence surrounded by double quotes). Some character sequences in the format have a special meaning: those beginning with the percent character (%) are interpreted as "placeholders" for the items contained in the argument list; moreover, special characters such as the newline character are represented via a combination beginning with a backslash.
For example, the code below
scalar x = sqrt(5)
string claim = sprintf("sqrt(%d) is (roughly) %6.4f.\n", 5, x)
print claim
will output
sqrt(5) is (roughly) 2.2361.
The expression %d in the format string indicates that we want an integer at that place in the output; since it is the leftmost "percent" expression, it is matched to the first argument, that is 5. The second special sequence is %6.4f, which stands for a decimal value at least 6 digits wide with 4 digits after the decimal separator. The number of such sequences must match the number of arguments following the format string.
See the help page for the printf command for more details about the syntax you can use in format strings.
| Argument: | x (scalar, series or matrix) |
Returns the positive square root of x; produces NA for negative values.
Note that if the argument is a matrix the operation is performed element by element. For the "matrix square root" see cholesky.
| Arguments: | L (list) |
| cross-products (boolean, optional) |
Returns a list that references the squares of the variables in the list L, named on the pattern sq_varname. If the optional second argument is present and has a non-zero value, the returned list also includes the cross-products of the elements of L; these are named on the pattern var1_var2. In these patterns the input variable names are truncated if need be, and the output names may be adjusted in case of duplication of names in the returned list.
Note that dummy variables will be skipped when computing squares to avoid producing an identical series, but their product (aka "interaction") with other series in the input list L will be computed.
| Arguments: | src (string or array of strings) |
| format (string) | |
| ... (see below) |
Reads values from src under the control of format and assigns these values to one or more trailing arguments, indicated by the dots above. Returns the number of values assigned. This is a simplified version of the sscanf function in the C programming language, with an extension to the scanning of an entire matrix (see "Scanning a matrix" below). Note that giving an array of strings as src is acceptable only in the case of matrix scanning.
src may be either a literal string, enclosed in double quotes, or the name of a predefined string variable. format is defined similarly to the format string in printf (more on this below). The trailing arguments—the names of predefined variables that are the targets of conversion— must be separated by commas. (For those used to C: one can prefix the names of numerical variables with an ampersand, as in &x but this is not required.)
Literal text in format is matched against src. Conversion specifiers start with %, and recognized conversions include %f, %g or %lf for floating-point numbers; %d for integers; and %s for strings. You may insert a positive integer after the percent sign: this sets the maximum number of characters to read for the given conversion. Alternatively, you can insert a literal asterisk, *, after the percent to suppress the conversion (thereby skipping any characters that would otherwise have been converted for the given type). For example, %3d converts the next 3 characters in src to an integer, if possible; %*g skips as many characters in src as could be converted to a single floating-point number.
Note that in the case of %s conversion for strings, scanning for a given argument stops when white space is encountered. For greater flexibility a simplified version of the C format %N[chars] is available. In this format N (which is optional) is the maximum number of characters to read and chars is a set of acceptable characters, enclosed in square brackets: reading stops if N is reached or if a character not in chars is encountered. The behavior of this construction is reversed if a circumflex, ^, is given as the first element of chars. In that case reading stops when a character in the given set is found. (Unlike C, the hyphen does not play a special role in the chars set.) For example,
string src = "some arbitary text that might be of interest" string s1 string s2 sscanf(src, "%s", s1) printf "s1 = '%s'\n", s1 sscanf(src, "%18[^\n]", s2) printf "s2 = '%s'\n", s2
The first scan yields "some" while the second gives "some arbitary text".
If the source string does not (fully) match the format, the number of conversions may fall short of the number of arguments given. This is not in itself an error so far as gretl is concerned. However, you may wish to check the number of conversions performed; this is given by the return value. A simple example follows:
# scanning scalar values
scalar x
scalar y
n = sscanf("123456", "%3d%3d", x, y)
printf "scanned %d values\n", n
Matrix scanning must be signaled by the special conversion specification "%m". The maximum number of rows to be read can be specified by inserting an integer between the "%" sign and the "m" for matrix. Two variants are supported: src a single string representing a matrix, and src an array of strings. We describe these options in turn.
If src is a single string argument the scanner reads a line of input and counts the number of space- or tab-separated numeric fields. This defines the number of columns in the matrix. By default, reading then proceeds for as many lines (rows) as contain the same number of numeric columns, but the maximum number of rows can be limited via the optional integer value mentioned above.
If src is an array of strings the output is necessarily a column vector, each element of which is the numerical conversion of the corresponding string, or NA if the string is not numeric. Here are some simple examples.
# scanning a single string
string s = sprintf("1 2 3 4\n5 6 7 8")
print s
matrix m
sscanf(s, "%m", m)
print m
# scanning an array of strings
strings S = defarray("1.1", "2.2", "3.3", "4.4", "5.5")
sscanf(S, "%4m", m)
print m
| Argument: | y (series or vector) |
Returns the sum of squared deviations from the mean for the non-missing observations in the series or vector y. See also var.
| Arguments: | L (list) |
| n (integer) | |
| offset (integer, optional) |
Designed for manipulation of data into the stacked time series format required by gretl for panel data. The return value is a series obtained by stacking "vertically" n observations from each series in the list L. By default the first n observations are used (corresponding to offset = 0) but the starting point can be shifted by supplying a positive value for offset. If the resulting series is longer than the existing dataset, observations are added as needed.
This function can handle the case where a data file holds side-by-side time series for a number of cross-sectional units, as well as the case where time runs horizontally and each row represents a cross-sectional unit.
See the section titled "Panel data specifics" in chapter 4 of the Gretl User's Guide for details and examples of usage.
| Arguments: | X (series, list or matrix) |
| v (integer, optional) | |
| skip_na (boolean, optional) |
By default, returns a standardized version of the series, list or matrix: the input is centered and divided by its sample standard deviation (with a degrees of freedom correction of 1). Results are computed by column in the case of matrix input.
The optional second argument can be used to inflect the result. A non-negative value of v sets the degrees of freedom correction used in the standard deviation, so v = 0 gives the maximum likelihood estimator. As a special case, if v equals –1 only centering is performed.
By default missing values are automatically skipped in the case of series or list input but not for matrix input. To have missing values ignored in the matrix case, supply a non-zero value for skip_na.
| Arguments: | epoch_day (scalar, series or matrix) |
| format (string, optional) |
This function works like strftime, converting from a numeric value to a string governed by format, except that the input is an "epoch day", for the definition of which see epochday. Since the resolution is daily, only date-related formats are handled; time-related formats give undefined results.
If the second argument is omitted the format defaults to ISO 8601 extended, YYYY-MM-DD.
| Arguments: | tm (scalar, series or matrix) |
| format (string, optional) | |
| offset (scalar, optional) |
The argument tm is taken to give "Unix time", the number of seconds since the start of the year 1970 according to UTC, and the return value is a string giving the corresponding date and/or time—either in a format specified via the optional second argument or, by default, the "preferred date and time representation for the current locale" as determined by the system C library. See below for more on the format specification.
The optional offset argument can be used to specify an offset in seconds relative to UTC, thus selecting a time zone other than the default, which is always local time. For example an offset of 3600 selects Central European Time, while 0 selects GMT. The absolute value of offset should not exceed 86400 (24 hours).
The specific type returned depends on that of tm: if tm is a scalar, vector, or series the output is, respectively, a single string, an array of strings, or a string-valued series.
Values of tm suitable for use with this function may be obtained via the $now accessor or the strptime function.
Note that while tm is taken as relative to UTC the output of this function is by default "local", relative to the time-zone setting on the host computer. A given tm will therefore show a different time, and perhaps a different date, in different time zones. But if you want a string representing UTC rather than local time, gretl can do that; see below.
The standard formatting options may be found by consulting the strftime manual page, on systems which have such pages, or via one of the many websites which present relevant information, such as https://devhints.io/strftime. In addition to the standard formats gretl recognizes a special option: if format is just "8601", date and time are shown in ISO 8601 format.
| Arguments: | y (series) |
| S (array of strings) |
Provides a means of defining string values for the series y. Two conditions must be satisfied for this to work: the target series must have nothing but integer values, none of them less than 1, and the array S must have at least n elements where n is the largest value in y. In addition each element of S must be valid UTF-8. If any of these conditions is not met, an error is flagged. The nominal return value is 0 on successful completion.
An alternative to stringify that may be useful in some contexts is direct assignment from an array of strings to a series: this creates a series whose values are taken from the array in sequence; the number of elements in the array must equal either the full length of the dataset or the length of the current sample range, and values may be repeated as required.
| Argument: | s (string or array of strings) |
If s is a single string, returns the number of UTF-8 characters it contains. Note that this will be less than the number of bytes if the string contains any multi-byte (non-ASCII) characters. If you want the number of bytes you can use the nelem function. For example:
string s = "¡Olé!" printf "strlen(s) = %d, nelem(s) = %d\n", strlen(s), nelem(s)
should return
strlen(s) = 5, nelem(s) = 7
If the argument is an array of strings the return value is a column vector holding the number of characters in each string. A string-valued series is also an acceptable argument: in this case the return value is a series holding the length of the string values over the current sample range.
| Arguments: | s1 (string) |
| s2 (string) | |
| n (integer, optional) |
Compares the two string arguments and returns an integer less than, equal to, or greater than zero if s1 is found, respectively, to be less than, to match, or be greater than s2, up to the first n characters. If n is omitted the comparison proceeds as far as possible.
Note that if you just want to compare two strings for equality, that can be done without using a function, as in if (s1 == s2) ...
| Arguments: | s (string, strings array or string-valued series) |
| format (string, optional) |
This function works just like strptime, except that the return value is an "epoch day" value, for the definition of which see epochday. Since the resolution is daily, any time-of-day information in s is ignored.
| Arguments: | s (string, strings array or string-valued series) |
| format (string, optional) |
This function is the converse of strftime; it parses one or more date/time strings using the specified format and returns the number of seconds since the start of 1970 according to Coordinated Universal Time (UTC). The specific type of the return value depends on that of s: if s is a string, strings array, or string-valued series the output is, respectively, a scalar, a column vector, or a numeric series.
If format is omitted, it defaults to ISO 8601 "extended", YYYY-MM-DD (which translates to "%Y-%m-%d" as a strptime format).
As a special case, the first argument may be given as an 8-digit integer conforming to the ISO 8601 "basic" date format, YYYYMMDD (or a vector or series containing such values). In that case format should be omitted.
Note that the first argument to this function is taken as relative to the time-zone setting on the host computer. So for example, the call
strptime("13/02/2009 23:31.30", "%d/%m/%Y %H:%M.%S")
will produce 1234567890 on output if your system time is set to UTC but if you're in the Central European time zone (UTC+01:00) the output will be 1234564290.
The format options may be found by consulting the strptime manual page, on systems which have such pages, or via one of the many websites which present relevant information, such as http://man7.org/linux/man-pages/man3/strptime.3.html.
The example below shows how one can convert date information from one format to another.
scalar tm = strptime("Thursday 02/07/19", "%A %m/%d/%y")
eval strftime(tm) # default output
eval strftime(tm, "%B %d, %Y")
On the East Coast of the USA the result is
Thu 07 Feb 2019 12:00:00 AM EST February 07, 2019
| Arguments: | s (string) |
| sep (string, optional) | |
| i (integer, optional) |
In basic usage, with a single argument, returns the array of strings that results from the splitting of s on white space (that is on any combination of the space, tab and/or newline characters).
The optional second argument can be used to specify the separator used for splitting s. For example
string basket = "banana,apple,jackfruit,orange" strings S = strsplit(basket, ",")
will split the input into an array of four strings using comma as separator.
The backslash-escape sequences "\n", "\r" and "\t" are taken to represent newline, carriage return and tab, respectively, in the optional sep argument. If you wish to include a literal backslash as a separator character you should double it, as in "\\". Example:
string s = "c:\fiddle\sticks" strings S = strsplit(s, "\\")
Regardless of the separator, the members of the returned array are trimmed of any leading or trailing white space. Correspondingly, if sep contains non-whitespace characters then it is stripped of any leading or trailing space.
If an integer value greater than zero is given as the third argument the return value is a single string, namely the (1-based) element i of the array that would otherwise be produced. If i is less than 1 that provokes an error, but if i is greater than the implied number of elements an empty string is returned.
| Arguments: | s1 (string) |
| s2 (string) | |
| ign_case (boolean, optional) |
Searches s1 for an occurrence of the string s2. If a match is found, returns a copy of the portion of s1 that starts with s2, otherwise returns an empty string.
Example:
string s1 = "Gretl is an econometrics package"
string s2 = strstr(s1, "an")
print s2
If the optional argument ign_case is nonzero, the search is case-insensitive. For example,
strstr("Chicago", "c")
returns "cago", but
strstr("Chicago", "c", 1)
returns "Chicago".
If you just wish to find out if s1 contains s2 (boolean test), see instring.
| Argument: | s (string) |
Returns a copy of the argument s from which leading and trailing white space have been removed.
Example:
string s1 = " A lot of white space. "
string s2 = strstrip(s1)
print s1 s2
| Arguments: | s (string, strings array or string-valued series) |
| find (string) | |
| subst (string) |
If s is a single string, returns a copy of s in which all occurrences of find are replaced by subst. If s is an array of strings or string-valued series this operation is performed on each string in the array or series. See also regsub for more complex string replacement via regular expressions.
Example:
string s1 = "Hello, Gretl!"
string s2 = strsub(s1, "Gretl", "Hansl")
print s2
| Arguments: | y (series) |
| subsample (boolean, optional) |
If the series y is string-valued, returns by default an array containing all its distinct values (irrespective of the current setting of the sample range), ordered by the associated numerical values starting at 1. If the dataset is currently subsampled you can give a non-zero value for the optional second argument to obtain an array holding just the string values present in the subsample.
If y is not string-valued an empty strings array is returned. See also stringify.
An alternative to strvals that may be useful in some contexts is direct assignment of a string-valued series to an array of strings: this provides not just the distinct values, but all values of the series in the current sample range.
| Arguments: | y (series) |
| S (array of strings, optional) |
Carries out one or other of two sorts of rearrangment of the series y, which must be string-valued. The nominal return value is 0 on successful completion.
Method 1: If the second argument is not given, the effect is to sort y in this sense: the distinct string values are alphabetized and then the series is recoded such that 1 is assigned for the first of the ordered strings, 2 for the second, and so on. This can be useful, among other reasons, for ensuring a uniform encoding for multiple series that share the same set of string values.
Method 2: If the second argument is given, it must be an array which contains exactly the distinct string values of y (which can be found via strvals), but put into a preferred order. Then the effect is to recode the series such that value 1 is assigned for the first string in S, value 2 for the second, and so on. This can be useful for ensuring that the numeric codes "make sense" when string values can be thought of as naturally ordered.
The primary use case for these methods is the handling of string-valued series imported from third-party sources such as comma-separated files. For such data, gretl assigns numeric codes based simply on the order of occurrence of the strings across the rows of the file. So in a series with values low, middle and high, high will be assigned code 1 if it happens to occur first, rather than 3, which would clearly be more "natural". This can be fixed using Method 2. Moreover, if two or more series share the same string values, they will be encoded differently unless their distinct values happen to appear in the same order in the data file. This could be fixed by either method.
| Arguments: | s (string, strings array or string-valued series) |
| start (integer) | |
| end (integer) |
If s is a single string, returns the substring of s from the character with (1-based) index start to that with index end, inclusive, or from start to the end of s if end is –1. If the argument is an array of strings or string-valued series, this operation is performed on each string in the array or series.
For example, the code below
string s1 = "Hello, Gretl!"
string s2 = substr(s1, 8, 12)
print s2
gives:
? print s2 Gretl
It should be noted that in some cases you may be willing to trade clarity for conciseness, and use slicing and increment operators, as in
string s1 = "Hello, Gretl!"
string s2 = s1[8:12]
string s3 = s1 + 7
print s2
print s3
which would give you
? print s2 Gretl ? print s3 Gretl!
| Arguments: | x (series, matrix or list) |
| partial (boolean, optional) |
If x is a series, returns the (scalar) sum of the non-missing observations in x. See also sumall.
If x is a matrix, returns the sum of the elements of the matrix.
If x is a list, returns a series y such that yt is the sum of the values of the variables in the list at observation t. By default the sum is recorded as NA if there are any missing values at t, but if you pass a non-zero value for partial any non-missing values will be used to form the sum.
| Argument: | x (series) |
Returns the sum of the observations of x over the current sample range, or NA if there are any missing values. Use sum if you want missing values to be skipped.
| Arguments: | X (matrix) |
| skip_na (boolean, optional) |
Returns the sums of the columns of X. If a non-zero value is given for the optional second argument missing values are ignored, otherwise the result is NA for any columns that contain missing values. See also meanc, sumr.
| Arguments: | X (matrix) |
| skip_na (boolean, optional) |
Returns the sums of the rows of X. If a non-zero value is given for the optional second argument missing values are ignored, otherwise the result is NA for any rows that contain missing values. See also meanr, sumc.
| Arguments: | X (matrix) |
| &U (reference to matrix, or null) | |
| &V (reference to matrix, or null) |
Performs the singular values decomposition of the matrix X.
The singular values are returned in a row vector. The left and/or right singular vectors U and V may be obtained by supplying non-null values for arguments 2 and 3, respectively. For any matrix A, the code
s = svd(A, &U, &V) B = (U .* s) * V
should yield B identical to A (apart from machine precision).
See also eigengen, eigensym, qrdecomp.
| Arguments: | L (list) |
| bparms (bundle) | |
| bmod (reference to bundle, optional) | |
| bprob (reference to bundle, optional) |
This function enables the training of, and prediction based on, an SVM (a Support Vector Machine), using LIBSVM as back-end. The list argument L should include the dependent variable followed by the independent variables and the bparms bundle is used to pass options to the SVM mechanism. The return value is a series holding the SVM's predictions. The two optional bundle-pointer argument can be used to retrieve additional information after training and/or prediction.
For details, please see the PDF documentation for gretl + SVM.
| Argument: | x (scalar, series or matrix) |
Returns the tangent of x. See also atan, cos, sin.
| Argument: | x (scalar, series or matrix) |
Returns the hyperbolic tangent of x.
| Arguments: | Y (series or matrix) |
| X (series, list or matrix, optional) | |
| s (scalar) | |
| opts (bundle, optional) | |
| results (bundle, optional) |
Performs temporal disaggregation (conversion to higher frequency) of the time-series data in Y. The argument s gives the expansion factor (for example, 3 for quarterly to monthly). The argument X may contain one or more covariates at the higher frequency to aid in the disaggregation. Several options may be passed in opts, and details of the disaggregation may be retrieved via results.
See chapter 9 of the Gretl User's Guide for details.
| Arguments: | x (scalar, series or matrix) |
| a (scalar, series or matrix) | |
| hard (scalar, optional) |
Performs soft or hard thresholding on x, depending on the value of the optional Boolean parameter hard, whose default value is 0.
In both cases, entries in x whose absolute value is less than a are set to 0. With soft thresholding, the other ones are shrunk towards 0. For example, the code below
s = seq(-2,2,0.5)' eval s ~ thresh(s, 0.5) ~ thresh(s, 0.5, 1)
produces
-2 -1.5 -2
-1.5 -1 -1.5
-1 -0.5 -1
-0.5 0 0
0 0 0
0.5 0 0
1 0.5 1
1.5 1 1.5
2 1.5 2
If the two arguments differ in type, the type of the result is the "higher" of the two, where the ordering is matrix > series > scalar. For example, if y is a scalar and x an n-vector (or vice versa) the result is an n-vector. Note that matrix arguments must be vectors, and if neither argument is a scalar the two arguments must be of the same length.
| Arguments: | c (vector) |
| r (vector) | |
| b (vector) | |
| &det (reference to scalar, optional) |
Solves a Toeplitz system of linear equations, that is Tx = b where T is a square matrix whose element Ti,j equals ci-j for i>=j and rj-i for i<=j. Note that the first elements of c and r must be equal, otherwise an error is returned. Upon successful completion, the function returns the vector x.
The algorithm used here takes advantage of the special structure of the matrix T, which makes it much more efficient than other unspecialized algorithms, especially for large problems. Warning: in certain cases, the function may spuriously issue a singularity error when in fact the matrix T is nonsingular; this problem, however, cannot arise when T is positive definite.
If the optional argument det is supplied (in pointer form), it will contain on exit the determinant of T. For example, the code:
A = unvech({3;2;1;3;2;3}) # Build a 3x3 Toeplitz matrix
x = ones(3,1) # and a 3x1 vector
print A x
eval A\x # solution via generic inversion
eval det(A) # print the determinant
a = A[1,]
d = 0
eval toepsolv(a, a, x, &d) # use the dedicated function
print d
produces
A (3 x 3)
3 2 1
2 3 2
1 2 3
x (3 x 1)
1
1
1
0.25000
-3.3307e-17
0.25000
8
0.25000
2.7756e-17
0.25000
d = 8.0000000
| Argument: | s (string, strings array or string-valued series) |
If s is a single string, returns a copy of s in which any upper-case characters are converted to lower case. If s is an array of strings or string-valued series this operation is performed on each string in the array or series.
Example:
string s1 = "Hello, Gretl!"
string s2 = tolower(s1)
print s2
| Argument: | s (string, strings array or string-valued series) |
If s is a single string, returns a copy of s in which any lower-case characters are converted to upper case. If s is an array of strings or string-valued series this operation is performed on each string in the array or series.
Examples:
string s1 = "Hello, Gretl!"
string s2 = toupper(s1)
print s2
| Argument: | A (square matrix) |
Returns the trace of the square matrix A, that is, the sum of its diagonal elements. See also diag.
| Argument: | X (matrix) |
Returns the transpose of X. Note: this is rarely used; in order to get the transpose of a matrix, in most cases you can just use the prime operator: X'.
| Argument: | x (scalar, series or matrix) |
Returns the trigamma function of x, that is the second derivative of the log of the Gamma function.
| Arguments: | X (matrix) |
| ttop (integer) | |
| tbot (integer) |
Returns a matrix that is a copy of X with ttop rows trimmed at the top and tbot rows trimmed at the bottom. The latter two arguments must be non-negative, and must sum to less than the total rows of X.
See also selifr.
| Argument: | expr (string) |
A convenience function which combines typeof and typestr, with a little value added. Basically, the following two statements are equivalent
eval typestr(typeof(x)) eval typename(x)
except that if expr names an array, typename returns the specific type of the array, as in
strings S = defarray("foo", "bar", "baz")
eval typestr(typeof(S)) # gives "array"
eval typename(S) # gives "strings"
| Argument: | expr (string) |
Returns a numeric code indicating the type of expr, if it names a currently defined variable, specifies a sub-object such as a bundle member or array element, or is a valid expression that could stand as the right-hand side of an assignment statement. The codes are 1 for scalar, 2 for series, 3 for matrix, 4 for string, 5 for bundle, 6 for array and 7 for list. A return value of 0 indicates that expr names no existing object, or more generally that an assignment with expr on the right-hand side would fail.
A few examples follow:
strings S = defarray("foo", "bar")
eval typeof(S) # gives 6 (array)
eval typeof(S[1]) # gives 4 (string)
eval typeof(S[7]) # gives 0 (out of bounds)
eval typeof(S[x]) # gives 0 (invalid index)
eval typeof(1+1) # gives 1 (scalar)
eval typeof(sqrt("foo")) # gives 0 (invalid)
The function typestr may be used to get the string corresponding to the return value from typeof, though if you just want the string result typename may be a more convenient alternative.
| Argument: | typecode (integer) |
Given a gretl type code (for example, obtained via typeof or inbundle), returns a string giving the name of the type. The mapping from codes to strings is: 1 = "scalar", 2 = "series", 3 = "matrix", 4 = "string", 5 = "bundle", 6 = "array", 7 = "list", and 0 = "null".
See also typename for an alternative.
| Arguments: | a (scalar) |
| b (scalar) |
Generates a series of uniform pseudo-random variates in the interval (a, b), or, if no arguments are supplied, in the interval (0,1). The algorithm used by default is the SIMD-oriented Fast Mersenne Twister developed by Saito and Matsumoto (2008).
See also randgen, normal, mnormal, muniform.
| Argument: | x (series or vector) |
Returns a vector containing the distinct non-missing elements of x, not sorted but in their order of appearance. See values for a variant that sorts the elements.
| Arguments: | v (vector) |
| d (scalar, optional) |
If the second argument is omitted, returns an n x n symmetric matrix obtained by rearranging the elements of v. The number of elements in v must be a triangular integer—i.e., a number k such that an integer n exists with the property k = n(n+1)/2. This is the inverse of the function vech.
If the argument d is given, the function returns an (n+1) x (n+1) matrix with the extra-diagonal entries filled with the elements of v as above. All the elements of the diagonal are set to d instead.
Example:
v = {1;2;3}
matrix one = unvech(v)
matrix two = unvech(v, 99)
print one two
returns
one (2 x 2)
1 2
2 3
two (3 x 3)
99 1 2
1 99 3
2 3 99
| Argument: | A (square matrix) |
Returns an n x n upper triangular matrix: the elements on and above the diagonal are equal to the corresponding elements of A; the remaining elements are zero.
See also lower.
| Arguments: | tau (scalar) |
| n (integer) | |
| niv (integer) | |
| itv (integer) |
P-values for the test statistic from the Dickey–Fuller unit-root test and the Engle–Granger cointegration test, as per James MacKinnon (1996).
The arguments are as follows: tau denotes the test statistic; n is the number of observations (or 0 for an asymptotic result); niv is the number of potentially cointegrated variables when testing for cointegration (or 1 for a univariate unit-root test); and itv is a code for the model specification: 1 for no constant, 2 for constant included, 3 for constant and linear trend, 4 for constant and quadratic trend.
Note that if the test regression is "augmented" with lags of the dependent variable, then you should give an n value of 0 to get an asymptotic result.
| Argument: | x (series or vector) |
Returns a vector containing the distinct elements of x sorted in ascending order, ignoring any missing values. If you wish to truncate the values to integers before applying this function, use the expression values(int(x)).
| Arguments: | x (series or list) |
| partial (boolean, optional) |
If x is a series, returns the (scalar) sample variance, skipping any missing observations.
If x is a list, returns a series y such that yt is the sample variance of the values of the variables in the list at observation t. By default the variance is recorded as NA if there are any missing values at t, but if you pass a non-zero value for partial any non-missing values will be used to form the statistic.
In each case the sum of squared deviations from the mean is divided by (n – 1) for n > 1. Otherwise the variance is given as zero if n = 1, or as NA if n = 0.
See also sd.
| Argument: | v (integer or list) |
If given an integer argument, returns the name of the variable with ID number v, or generates an error if there is no such variable.
If given a list argument, returns a string containing the names of the variables in the list, separated by commas. If the supplied list is empty, so is the returned string. To get an array of strings as return value, use varnames instead.
Example:
open broiler.gdt
string s = varname(7)
print s
| Argument: | L (list) |
Returns an array of strings containing the names of the variables in the list L. If the supplied list is empty, so is the returned array.
Example:
open keane.gdt
list L = year wage status
strings S = varnames(L)
eval S[1]
eval S[2]
eval S[3]
| Argument: | varname (string) |
Returns the ID number of the variable called varname, or NA is there is no such variable.
| Arguments: | A (matrix) |
| U (matrix) | |
| y0 (matrix) |
Simulates a p-order n-variable VAR, that is y(t) = A1 y(t-1) + ... + Ap y(t-p) + u(t). The coefficient matrix A is composed by stacking the Ai matrices horizontally; it is n x np, with one row per equation. This corresponds to the first n rows of the matrix $compan provided by the var and vecm commands.
The u_t vectors are contained (as rows) in U (T x n). Initial values are in y0 (p x n).
If the VAR contains deterministic terms and/or exogenous regressors, these can be handled by folding them into the U matrix: each row of U then becomes u(t) = B'x(t) + e(t).
The output matrix has T + p rows and n columns; it holds the initial p values of the endogenous variables plus T simulated values.
| Argument: | X (matrix) |
Stacks the columns of X as a column vector. See also mshape, unvech, vech.
| Arguments: | A (square matrix) |
| omit-diag (boolean, optional) |
This function rearranges the the elements of A on and above the diagonal into a column vector, unless the omit-diag is given a non-zero value, in which case only the entries above the diagonal are considered.
Typically, this function is used on symmetric matrices, in which case it can be undone by the function unvech. If the input matrix is not symmetric and it's the lower triangle that contains the "right" values, vech(A') will give the desired answer (its elements may have to be re-ordered, however). See also vec.
| Arguments: | A (matrix) |
| K (matrix, optional) | |
| horizon (integer, optional) |
This function yields the VMA representation for a VAR system. If y(t) = A1 y(t-1) + ... + Ap y(t-p) + u(t), where ut are the one-step-ahead prediction errors, the corresponding VMA representation is y(t) = C0 e(t) + C1 e(t-1) + .... The relationship between the forecast errors ut and the structural shocks et is given by u(t) = K e(t). (Note that C0 = K.)
The coefficient matrix A is composed by stacking the Ai matrices horizontally; it is n x np, with one row per equation. This corresponds to the first n rows of the matrix $compan provided by gretl's var and vecm commands. The K matrix is optional, and defaults to the identity matrix if omitted.
The returned matrix will have horizon rows and n2 columns: its i-th row contains Ci-1 in vectorized form. The horizon value defaults to 24 if omitted.
See also irf.
| Arguments: | year (scalar or series) |
| month (scalar or series) | |
| day (scalar or series) |
Returns the day of the week (from Sunday = 0 to Saturday = 6) for the date(s) specified by the three arguments, or NA if the date is invalid. Note that all three arguments must be of the same type, either scalars (integers) or series.
An alternative call is also supported: if a single argument is given, it is taken to be a date (or series of dates) in ISO 8601 "basic" numeric format, YYYYMMDD. So the following two calls produce the same result, namely 2 (Tuesday).
eval weekday(1990, 5, 1) eval weekday(19900501)
A common alternative numbering for days of the week runs from Monday = 1 to Sunday = 7. If you have a series named wd obtained via weekday and you want to convert to the alternative you can do
altwd = wd == 0 ? 7 : wd
Note that if you simply add 1 to wd you get a numbering that's valid but non-standard, namely Sunday = 1 to Saturday = 7.
| Arguments: | Y (list) |
| W (list) | |
| partial (boolean, optional) |
Returns a series y such that yt is the weighted mean of the values of the variables in list Y at observation t, the respective weights given by the values of the variables in list W at t. The weights can therefore be time-varying. The lists Y and W must be of the same length and the weights must be non-negative.
By default the result is NA if any values are missing at observation t, but if you pass a non-zero value for partial any non-missing values will be used.
| Arguments: | Y (list) |
| W (list) | |
| partial (boolean, optional) |
Returns a series y such that yt is the weighted sample standard deviation of the values of the variables in list Y at observation t, the respective weights given by the values of the variables in list W at t. The weights can therefore be time-varying. The lists Y and W must be of the same length and the weights must be non-negative.
By default the result is NA if any values are missing at observation t, but if you pass a non-zero value for partial any non-missing values will be used.
| Arguments: | X (list) |
| W (list) | |
| partial (boolean, optional) |
Returns a series y such that yt is the weighted sample variance of the values of the variables in list X at observation t, the respective weights given by the values of the variables in list W at t. The weights can therefore be time-varying. The lists Y and W must be of the same length and the weights must be non-negative.
By default the result is NA if any values are missing at observation t, but if you pass a non-zero value for partial any non-missing values will be used.
| Arguments: | buf (string) |
| path (string or array of strings) | |
| &matches (reference to scalar, optional) |
The argument buf should be an XML buffer, as may be retrieved from a suitable website via the curl function (or read from file via readfile), and the path argument should be either a single XPath specification or an array of such.
This function returns a string representing the data found in the XML buffer at the specified path. If multiple nodes match the path expression the items of data are printed one per line in the returned string. If an array of paths is given as the second argument the returned string takes the form of a comma-separated buffer, with column i holding the matches from path i. In this case if a string obtained from the XML buffer contains any spaces or commas it is wrapped in double quotes.
By default an error is flagged if path is not matched in the XML buffer, but this behavior is modified if you pass the third, optional argument: in that case the argument retrieves a count of the matches and an empty string is returned if there are none. Example call:
ngot = 0 ret = xmlget(xbuf, "//some/thing", &ngot)
However, an error is still flagged in case of a malformed query.
A good introduction to XPath usage and syntax can be found at https://www.w3schools.com/xml/xml_xpath.asp. The back-end for xmlget is provided by the xpath module of libxml2, which supports XPath 1.0 but not XPath 2.0.
| Argument: | x (scalar, series or matrix) |
Converts zeros to NAs. If x is a series or matrix, the conversion is done element by element. See also missing, misszero, ok.
| Arguments: | r (integer) |
| c (integer, optional) |
Outputs a zero matrix with r rows and c columns. If omitted, the number of columns defaults to 1 (column vector). See also ones, seq.